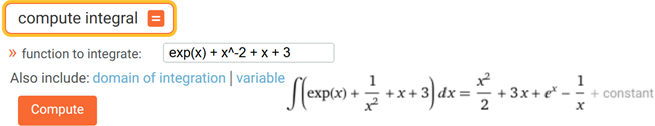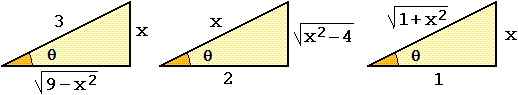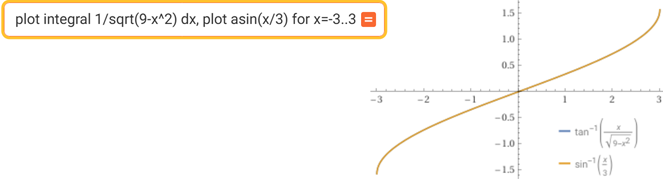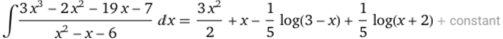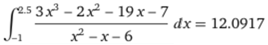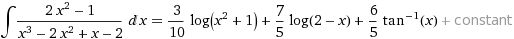Calcolo degli integrali

  Alla voce  integrale abbiamo visto se f è una funzione continua in [a, b] o è ivi limitata e discontinua in al più un numero finito di punti, allora esiste ∫_{[a, b]} f  (abbiamo anche richiamato la possibilità di usare metodi di calcolo approssimato per calcolare gli integrali in un dato intervallo).
    Se inoltre f è periodica abbiamo visto che, se T è il periodo ed I e J sono due intervalli ampi T, allora  ∫ _I f = ∫ _J f.
    Si è poi visto che se f e g sono integrabili su [a, b] allora  ∫_{[a, b]} f + g = ∫_{[a, b]} f + ∫_{[a, b]} g  e  ∫_{[a, b]} f − g = ∫_{[a, b]} f − ∫_{[a, b]} g,  e che se k è un numero qualunque  ∫_{[a, b]} k f = k ∫_{[a, b]} f .
    Abbiamo, poi, posto  ∫_{[b, a]} f = − ∫_{[a, b]} f,  e abbiamo visto che, se f è integrabile tra a e b, tra b e c, e tra a e c,  ∫ _{[a, b]} f + ∫ _{[b, c]} f = ∫ _{[a, c]} f
    Infine abbiamo considerato la formula fondamentale del calcolo integrale:

se f è continua in [a, b] e  G' = f  allora  ∫ _{[a, b]} f = G(b) − G(a).

∫ _{[1, 3]} 1/t dt = ?   D_x log(x) = 1/x;   ∫ _{[1, 3]} 1/t dt = [log(x)]_x=3 − [log(x)]_x=1 = log(3) − log(1) = log(3).

    Abbiamo, infine, introdotto    ∫ f(x) dx  per indicare un generico termine g(x) tale che g'(x) = f(x);  l'operazione che ad f(x) associa tale termine viene chiamata integrazione indefinita, mentre l'aggettivo definita viene riservato all'associazione alla funzione e ad un intervallo [a, b] del numero ∫ _{[a, b]} f.
    Qualche volta scriviamo  ∫ f(x) dx = g(x) e qualche altra volta  ∫ f(x) dx = g(x) + c,  per esplicitare che tutti i termini g(x) + c, al variare di c in IR, hanno per derivata (rispetto ad x) f(x)  (ricordiamo che in qualche caso si usano "+ c₁", "+ c₂", … per intervalli diversi).

    Ad esempio per trovare  ∫ (e^x + x⁻² + x + 3) dx  cerco f tale che df / dx = e^x + x⁻² + x + 3.  Quindi va bene  f(x) = e^x − x⁻¹ + x²/2 + 3x  e, più in generale,  f(x) = e^x − x⁻¹ + x²/2 + 3x + c  al variare di c in IR.

    Ricordiamo che con WolframAlpha si possono calcolare, in molti casi, gli integrali definiti e indefiniti:

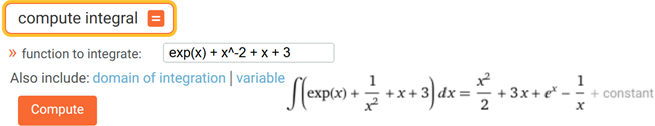
    Abbiamo, poi, visto che, mentre se integro una funzione polinomiale ottengo ancora una funzione polinomiale  ( ad es. se F(x) = 3x²+x−3√2  ho che  ∫ F(x) dx = x³+x²/2−3√2x+c, al variare di c in IR ),  in generale, di fronte a una cosiddetta funzione elementare  (ottenibile mediante successive composizioni di funzioni polinomiali, di elevamento a potenza, esponenziali, logaritmiche, circolari e circolari inverse)  non siamo sempre in grado di esprimerne mediante una formula analoga la funzione integrale.  Ad es. di fronte a F(x) = e^x2 so che F'(x) = 2x e^x2 ma non riesco a trovare alcuna funzione elementare la cui derivata sia F(x).
    In questa voce vedremo alcuni "trucchi", alcuni più significativi altri meno (e, comunque, ormai incorporati in vari tipi di software), per trovare, in molti casi, l'integrale di una funzione data.

  Integrazione per parti

Questo "trucco" si basa su una riscrittura della regola della derivazione del prodotto (  propr. f. cont. e derivabili):
D(f·g) = D(f)·g + g·D(f)  →  g·D(f) = D(f·g) − D(f)·g  →  ∫g·D(f) = f·g − ∫D(f)·g
    Un esempio:

∫ x e^x dx   Idea: è il prodotto di due termini, x ed e^x, dei quali il primo ha una derivata più semplice [D_x(x) = 1]  e il secondo può essere interpretato facilmente come la derivata di un altro termine [e^x = D_x(e^x) = e^x]. Quindi:
∫ x e^x dx = ∫ x D_x(e^x) dx = x e^x − ∫ D_x(x) e^x dx = x e^x − ∫ e^x dx = x e^x − e^x (+ c)

    Posso controllare l'esito con WolframAlpha:   integral x*exp(x) dx   →   exp(x)·(x-1) ( + c)

∫ x² e^x dx   D_x(x²) = 2x, quindi  ∫ x² e^x dx = ∫ x² D_x(e^x) dx = x² e^x - ∫ 2x e^x dx =  (↑)  x² e^x - 2(x e^x − e^x) = e^x·(x²-2x+2)
    Con WolframAlpha:   integral x^2·exp(x) dx   →   exp(x)·(x^2-2x+2) ( + c)

    A volte è utile il trucco di immaginare la presenza di un fattore "·1" da interpretare come D(f):
∫ log(x) dx = ∫ 1·log(x) dx = ∫ D_x(x)·log(x) dx = x·log(x) − ∫ x·D_x(log(x)) dx = x·log(x) − ∫1 dx = x·log(x) − x  (+ c)
    Con WolframAlpha:   integral log(x) dx   →   x (log(x) - 1) ( + c)

    Con WolframAlpha potrei tracciare anche il grafico dell'integranda e dell'integrale, ma ...

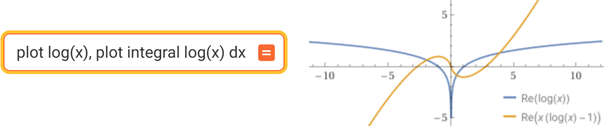
... occorre stare attenti: in questo caso si ottiene anche il grafico dove la funzione non è definita.  Il motivo è che il software opera in un ambiente più grande di quello dell'insieme dei numeri reali (nell'ambiente dei   numeri complessi):  occorre controllare il grafico ottenuto ed eventualmente non considerare le parti in cui le funzioni coinvolte non sono definite. In questo caso occorre escludere la parte a sinistra dell'asse y  (nei grafici appare "Re(...)" che sta a indicare la "parte reale", nel senso che le funzioni hanno anche una componente "complessa", che a noi comunque non interessa).

    Altre volte è utile il trucco di usare l'integrazione per parti per esprimere l'integrale in funzione di sé stesso, e quindi risolvere l'equazione ottenuta:
∫ log(x)/x dx = ∫ 1/x·log(x) dx = ∫ D_x(log(x))·log(x) dx = log(x)·log(x) − ∫ log(x)/x dx
da cui  2 ∫ log(x)/x = log(x)², e quindi  ∫ log(x)/x dx = log(x)²/2
    Con WolframAlpha:   integral log(x)/x dx   →   (log^2(x))/2 ( + c)

    In alcuni casi è necessario intergrare per parti più volte:
∫ e^xcos(x) dx = ∫ D_x(e^x) cos(x) dx = e^xcos(x) − ∫ e^xsin(x) dx
In modo analogo   ∫ e^xsin(x) dx = ∫ D_x(e^x) sin(x) dx = e^xsin(x) − ∫ e^xcos(x) dx
Quindi   2 ∫ e^xcos(x) dx = e^xcos(x) + e^xsin(x) (+ c)   da cui  ∫ e^xcos(x) dx = e^x (cos(x) + sin(x)) / 2 (+ c)
( verifica: D_x (e^x (cos(x)+sin(x))/2) = ... = e^x cos(x) 
    Con WolframAlpha:   integral exp(x) cos(x) dx   →   1/2 e^x (sin(x) + cos(x)) ( + c)

    Ecco un esempio di integrazione per parti di un integrale definito:
∫ _{[0, 1]} arctan(x) dx   Osserviamo, innanzi tutto, che la funzione integranda è definita e continua su tutto IR e, quindi, su [0, 1]. Quindi ha senso l'esercizio. Troviamo, prima, l'integrale indefinito. Procedendo per parti:  ∫ arctan(x) dx = ∫ D_x(x) arctan(x) dx = x·arctan(x) − ∫ x·1/(1+x²) dx = #   Ricordo che:   D(log(f(.)) = 1/f · D(f).  Quindi:   # = x·arctan(x) − log(1+x²)/2.  Infine:   ∫ _{[0, 1]} arctan(x) dx = [x·arctan(x)] _x=0..1 − [log(1+x²)/2] _x=0..1 = π/4 − log(2) / 2.
    Con WolframAlpha:   integral arctan(x) dx x=0..1   →   1/4 (π-log(4)) ≈ 0.43882  [log(4) = 2 log(2)].

Esercizi:   testo01  e  soluzione,   testo02  e  soluzione,   testo03  e  soluzione,   testo04  e  soluzione

  Integrazione per sostituzione

Questo è il più importante metodo di integrazione. Esso si basa sulla regola della derivazione delle funzioni composte. Partiamo da un esempio abbastanza semplice.

• ∫ sin(3x) dx    posso affrontarlo con la sostituzione t = 3x, da cui cui dt/dx = 3, dx = dt/3:
  ∫ sin(3x) dx = 1/3 · ∫ sin(t) dt = -cos(t)/3 = -cos(3x)/3 (+c)
    Con WolframAlpha:   integral sin(3 x) dx = -1/3 cos(3 x) (+c)

• ∫ 2x(x²−1)⁴ dx  posso affrontarlo con la sostituzione u = x²−1, du/dx = 2, du = 2x dx:
  ∫ 2x(x²−1)⁴ dx = ∫ u⁴ du = u⁵/5 = (x²−1)⁵/5 (+c)
  Posso controllare con WolframAlpha digitando  integral 2*x*(x^2-1)^4 dx

• ∫ tan(x) dx   Proviamo a risolverlo con WolfamAlpha. Otteniamo:

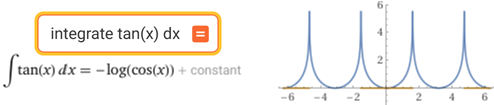
Ma  -log(cos(x))  è definito solo quando  cos(x)>0  e del resto il grafico che mostra che il software è definito ovunque cos(x) sia diverso da 0.  Nel caso di integrali di funzioni definite su unioni di intervalli il software non è detto che dia tutte le risposte.  In questo caso si perdono le soluzioni  -log(-cos(x)) (+ costante).

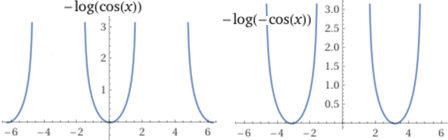
    Qualcosa di analogo accade per  ∫ 1/x dx, come già visto ( integrale)

    Torniamo a  ∫ tan(x) dx.

• ∫ x √(x−3) dx   In questo caso non è evidente se procedendo per sostituzione si riesce a calcolare l'integrale. Proviamo.
Pongo  u = x−3.  du = dx,  x = u+3.  ∫ (u+3)√u du = ∫ u^3/2+3u^1/2 du = 2/5 u^5/2 + 2 u^3/2  Quindi:  ∫ x √(x−3) dx = 2/5 (x−3)^5/2 + 2 (x−3)^3/2 (+ C).

• ∫ (1+e^x)/(1−e^x) dx   Ci conviene tracciare prima il grafico della integranda:

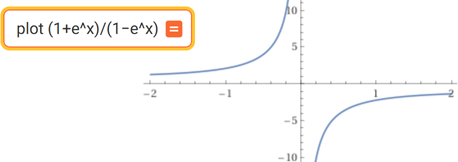
    Procediamo. La presenza preponderante di e^x mi suggerisce la sostituzione u = e^x, ossia x = log(u).
dx = 1/u du;   allora ottengo:   ∫(1+u)/(1-u) 1/u du
A questo punto cerco di sbarazzarmi del rapporto tra polinomi di grado 1:
(1+u)/(1−u) 1/u = (1−u+u+u)/(1−u) 1/u = (1 + 2u/(1−u)) 1/u = 1/u + 2/(1−u)
∫(1+u)/(1−u) 1/u du = log(u) − 2 log(1−u)
∫(1+e^x)/(1−e^x) dx = log(e^x) − 2 log(1−e^x) = x − 2 log(1−e^x)  (+c)
    Se provassi a fare il calcolo con WolframAlpha otterrei:

    Entrambe le funzioni sono soluzioni del nostro integrale: una lo è a sinistra di 0, l'altra a destra.  Sia il procedimento "manuale" che quello al computer hanno trascurato dei casi.  Il tracciamento del grafico della funzione e delle soluzioni (o l'immaginarli) ci è di aiuto per capire la situazione, e che le soluzioni sono:
x − 2 log(1−e^x)  (+c₁)     x − 2 log(e^x−1)  (+c₂)
    Questo è un problema tipico in cui affidandosi al solo calcolo è facile commettere errori (qui l'errore è stato non tener conto che ∫ 1/x dx è, a meno di costanti additive, log(|x|), non log(x), come si è già visto ( integrale).

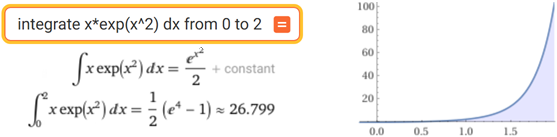
• Ecco un esempio di integrazione per sostituzione di un integrale definito:

∫ _{[0, 2]} x e^x2dx   Prima calcoliamo l'integrale indefinito. Poniamo u = x².  du = 2x dx.  ∫ e^u/2 du = e^u/2.  Quindi:  ∫ x e^x2dx = e^x2/ 2 (+ C).  Infine:  ∫ _{[0, 2]} x e^x2dx = [e^x2/ 2]_x=2 − [e^x2/ 2]_x=0 = (e⁴−1)/2.  Posto u = x², potevo procedere anche nel modo seguente.
∫ _{[0, 2]} x e^x2dx = ∫ _{[0, 4]} e^u/ 2 du  in quanto, per x che varia tra 0 e 2, u = x² varia tra 0 e 4.
Questo secondo metodo funziona quando du/dx (2x in questo caso) è funzione continua di x. Per un semplice controesempio si pensi a ∫ _[−1,1] |x| dx, che vale evidentemente 1 (è l'area di mezzo quadrato di diagonale 2). Con la sostituzione u = |x| mi ricondurrei ad un integrale tra 1 ed 1, che vale 0.

• Ricordiamo, infine, che se l'integranda è una funzione razionale di sin e/o di cos può essere comoda la sostituzione  t = tan(x/2):

∫ 1/(2+cos(x)) dx = (*)     t = tan(x/2),  cos(x) = (1−t²)/(1+t²),  dx = 2dt/(1+t²)
∫ 2dt/(1+t²) / ((3+t²)/(1+t²)) = 2 ∫ 1/(3+t²) dt = 2/√3 atan(t/√3)    (*) = 2/√3 atan(tan(x/2)/√3)

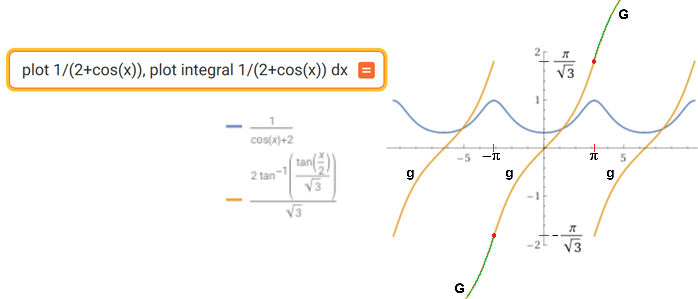
Occorre, però, stare attenti al dominio (come anche in altri casi di integrazione). Nel nostro caso la soluzione proposta  (g(x) = 2/√3 atan(tan(x/2)/√3), rappresentata sopra dai tratti di colore arancione)  non è definita su tutto IR, come lo è invece la funzione intergranda.  Ad esempio la soluzione che in 0 vale 0  coincide in (−π, π) con la funzione rappresentata sopra al centro.  Ma per x → π−  g(x) → π/√3;  analogamente per x → −π+  g(x) → −π/√3.  Posso estendere tale funzione ad una soluzione definita su tutto IR ponendo g(π) = π/√3, g(−π) = −π/√3 e poi prolungandola per continuità nel modo sopra raffigurato in verde, ossia traslando verticalmente gli altri tratti di curva di colore arancione;  ad es. per x in (π, 2π) prendendo y = g(x)+2π/√3.  Chiamiamo G tale funzione.  Le altre soluzioni sono  G(x) + C  al variare di C in IR.  Sarebbe, quindi, sbagliato scrivere che le soluzioni sono 2/√3 atan(tan(x/2)/√3) + C.

Esercizi:   testo05 e sol.   testo06 e sol.   testo07 e sol.   testo08 e sol.   testo09 e sol.   testo10 e sol.   testo11 e sol.   testo12 e sol.
 

  Approfondimenti.  Integrazione per sostituzione trigonometrica

Esisitono alcuni "trucchi" per calcolare con sostituzione alcuni tipi particolari di integrali, in cui si utilizzano le relazioni tra gli elementi di un triangolo rettangolo (tuttavia, anche in questi casi, esiste del software che esegue automaticamente i calcoli).  Facciamo degli esempi, riferendoci alle figure seguenti (che valgono solo per x e θ positivi, ma suggeriscono relazioni che possono valere anche per x e θ negativi).

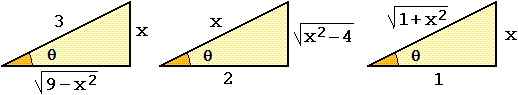
• ∫ 1/√(9−x²) dx     può essere affrontato (vedi figura a sinistra) pensando a  √(9−x²) = 3·cos(θ),  x = 3·sin(θ),  dx = 3·cos(θ) dθ
∫ 3·cos(θ) / (3·cos(θ)) dθ = ∫ 1 dθ = θ
∫ 1/√(9−x²) dx = asin(x/3)  (+c)    Sotto il controllo "grafico" con WolframAlpha (i due grafici si sovrappongono):

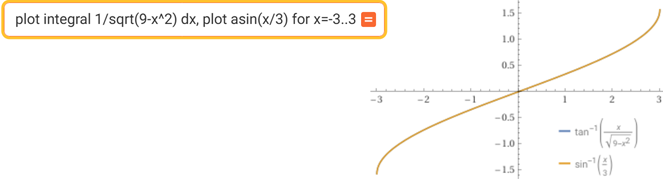
    Sotto anche il grafico dell'integranda (l'integrale da WolframAlpha viene espresso con una formula diversa, ma equivalente):

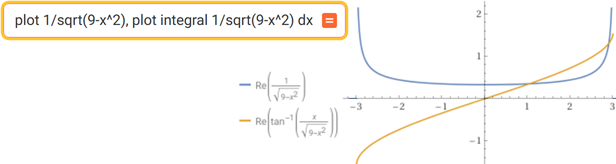
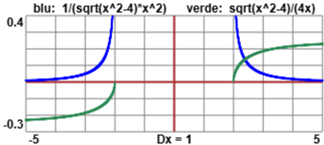
• ∫ 1 / ( √(x²−4) x² ) dx     può essere affrontato (vedi la figura iniziale al centro) pensando a  √(x²−4) = 2·tan(θ),  2/x = cos(θ), da cui  x = 2/cos(θ), dx = 2·tan(θ)/cos(θ) dθ.

Quindi  ∫ 1 / (2·tan(θ)·4/cos(θ)2)·2·tan(θ)/cos(θ) dθ = ∫ 1/4 cos(θ) dθ = sin(θ)/4 (+c) ∫ 1 / ( √(x2−4) x2 ) dx = √(x2−4) / (4x) (+c) Sotto il grafico ottenuto con questo script.

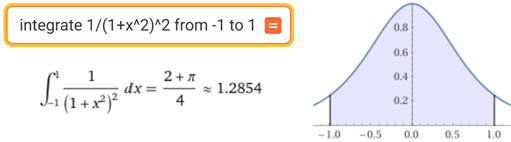
• ∫ _{[−1, 1]} 1 / (1+x²)² dx   è un integrale definito che possiamo affrontare considerando il triangolo rettangolo raffigurato nella figura iniziale a destra:
x = tan(θ),  1/√(1+x²) = cos(θ),  dx = 1/cos(θ)² dθ.  Per x che varia tra −1 e 1  θ varia tra −π/4 e π/4.
∫ _{[−1, 1]} 1 / (1+x²)² dx = ∫ _{[−π/4, π/4]} cos(θ)⁴ / cos(θ)² dθ = ∫ _{[−π/4, π/4]} cos(θ)² dθ = ∫ _{[−π/4, π/4]} (1−cos(2θ))/2 dθ = [(θ+sin(2θ)/2)/2] _{θ = −π/4 .. π/4} = π/4 + 1/2.

    Controllo con WolframAlpha:

Esercizio:     testo13  e  soluzione

  Approfondimenti.  Integrazione di funzioni razionali

Illustriamo, utilizzando WolframAlpha, i procedimenti che si possono impiegare per integrare le cosiddette funzioni razionali, ossia le funzioni esprimibili come rapporto tra funzioni polinomiali, attraverso un paio di esempi.

•	∫   3x3−2x2−19x−7  dx ——————— x2−x−6

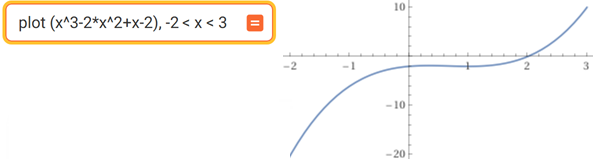
Innanzi tutto tracciamo il grafico dell'integranda:

plot (3x^3-2x^2-19x-7) / (x^2-x-6), x = -4..4

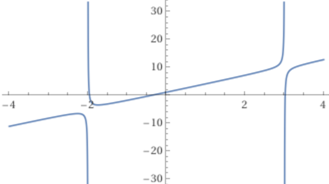
L'integranda non è definita in -2 e in 3. Utlizzando il comando compute integral mettendo in input  (3x^3-2x^2-19x-7) / (x^2-x-6)  ottengo:

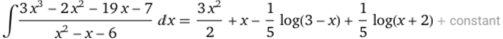
Questa è l'espressione dell'integrale nell'intervallo centrale, tra -2 e 3 (dove log(x+2) e log(3-x) sono definite.  L'integrale in questo e negli altri intervalli, a meno di costanti additive, è  x + (3*x^2)/2 - 1/5*log(|3 - x|) + 1/5*log(|2 + x|)  (vedi qui).

Se voglio uno schizzo della funzione integrale (a meno delle costanti additive) posso usare il comando  plot x + (3 x^2)/2 - 1/5 log(|3 - x|) + 1/5 log(|2 + x|), x = -2.5..3.5

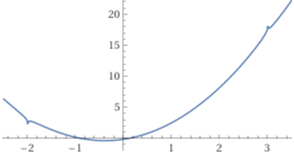
In casi di funzioni come questa, quello che può capitare in qualche applicazione è calcolare degli integrali definiti. Usando  compute integral  calcoliamo l'integrale tra -1 e 2.5:

function to integrate:  (3x^3-2x^2-19x-7) / (x^2-x-6) lower limit:  -1 upper limit:  2.5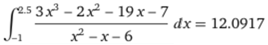

•	∫   2x2−1  dx ——————— x3−2x2+x-2

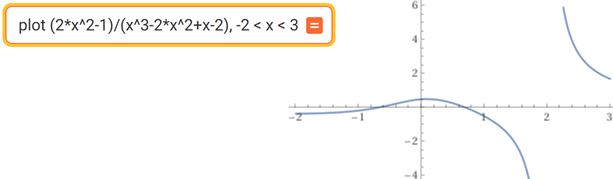
Usando  compute integral:

function to integrate:  (2*x^2-1)/(x^3-2*x^2+x-2)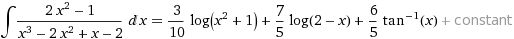

plot 6/5 tan^(-1)(x) + 7/5 log(|2 - x|) + 3/10 log(1 + x^2), -5 < x < 5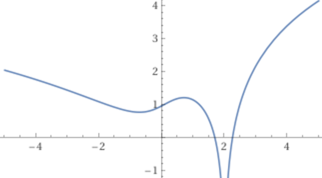

    Si può dimostrare che ogni funzione razionale è integrabile mediante una combinazione lineare di funzioni razionali e di funzioni del tipo log(F(.)) e atn(F(.)) con F polinomio di primo o secondo grado.

Esercizi:   testo14  e  soluzione,     testo15  e  soluzione

  Esiste vario software che calcola "simbolicamente" gli integrali indefiniti. Però, spesso, non dà tutte le soluzioni o ne dà alcune che valgono solo per particolari intervalli. Del resto, problemi analoghi valgono anche per alcuni procedimenti manuali suggeriti da alcuni libri.  Lo studio dei domini, il controllo grafico e/o simbolico di quanto si ottiene sono, dunque, fondamentali.

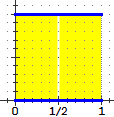
Osserviamo, infine, che accanto al concetto di integrale considerato qui, esistono altri concetti di integrazione, che consentono di definire l'area di altre superfici.  Consideriamo, ad esempio, la figura costituita dal quadrato che ha per lati i segmenti da 0 ad 1 dei due assi e privata dei segmenti costituiti dai punti di ascissa razionale; si può dimostrare (vedi questi esercizi) che questi segmenti sono una infinità numerabile, trascurabile rispetto al complesso del quadrato; l'area di questa figura non può comunque essere calcolata mediante il concetto di integrale introdotto ( vedi). Attraverso un concetto più generale di integrale si può invece ottenere anche per tale figura, come per l'intero quadrato, che essa ha area 1. Chi proseguirà gli studi in matematica o fisica, o in corsi di laurea simili, studierà queste generalizzazioni, che hanno applicazioni in vari campi.