Indichiamo con T1 e T2 i due termini
√(x2+1)-x
e
1/(√(x2+1)+x).
Alcune possibili uscite:
x T1 T2
1234 0.0004051863193126337 0.00040518631921557805
12345 0.00004050222742080223 0.00004050222755607815
123456 0.000004050030838698149 0.000004050025920099458
1234567 4.048924893140793e-7 4.0500029565014935e-7
12345678 4.0978193283081054e-8 4.0500003321000205e-8
123456789 0 4.050000036855001e-9
Man mano che aumento x, moltiplicando circa per 10, per un po' sia T1 che T2
si riducono, dividendosi circa per 10. Del resto, al crescere dell'ordine di grandezza di x
il valore di x2+1 tende a coincidere per sempre più cifre significative
con quello di x2, e quindi T2 tende a coincidere con 1/(2x), ossia
a un termine inversamente proporzionale a x.
Il fatto che da un certo punto in poi T1 si scosti da questo comportamento suggerisce che siano
intervenuti errori di approssimazione tali da rendere non attendibili i
valori visualizzati.
Se rappresentassi graficamente (ad es. con WolframAlpha)
l'andamento dei due termini in funzione di x, per valori di x tra due successive
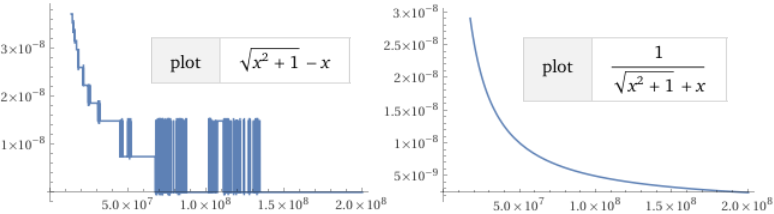
potenze di 10, prima o poi assisterei ad un andamento simile al seguente, il quale confermerebbe che T2
(il termine che "scolasticamente" sarebbe considerato più brutto: molti libri scolastici lo fanno "razionalizzare" in T1),
è quello migliore dal punto di vista del calcolo: le strane oscillazioni del grafico di T1 e il suo brutale spiaccicarsi
sull'asse x corrispondono all'intervento degli errori di approssimazione.
plot 1/(sqrt(x^2+1)+x) for 2e6 < x < 2e8
plot sqrt(x^2+1)-x for 2e6 < x < 2e8
I problemi per T1 nascono dal fatto che per x con ordine di grandezza grande √(x2+1) e x tendono
ad assumere valori sempre più vicini per cui, da un certo punto in poi, interviene
il fenomeno della cancellazione delle cifre.
Per altri commenti:
Calcolatore-6
Nota. Anche per studiare l'ordine di infinitesimo di T1 rispetto a 1/x (per x → ∞) è utile trasformarlo
nella forma "brutta" T2.