Calcolatore (6) - I numeri macchina

  Precisione dei risultati
    Nella voce  strutture numeriche e non abbiamo visto che i numeri macchina di una CT costituiscono una struttura per vari aspetti diversa da quella dei numeri reali: è costituita da una quantità finita di elementi, ha operazioni diverse (12345678·0. 12345678 per la moltiplicazione tra numeri reali è pari a 1524157.65279684, per una CT che arrotonda a 8 cifre è pari a 1524157.7), non valgono alcune proprietà, anche elementari, come quella del riordino di una somma:
il calcolo di  –12345678 [+] 12345678 [+] 0. 12345678 [=]
e quello di   –12345678 [+] 0 .12345678 [+] 12345678 [=]
per una CT che arrotonda a 10 cifre non sono equivalenti:  mentre il primo dà 0 .12345678 il secondo dà 0 .12;  infatti -12345678+0 .12345678 (= -12345677.87654322) viene arrotondato a -12345677.88, che, sommato a 12345678, fa appunto 0 .12.
    Dunque, nell'eseguire un calcolo complesso con una CT è utile analizzare il termine da calcolare ed eventualmente trasformarlo, non solo per facilitare l'impostazione del calcolo (vedi le voci richiamate nell'indice alfabetico sotto "calcolatrice tascabile e trasformazione di formule"), ma anche per ottenere risultati con una migliore precisone.
    Le calcolatrici incorporate negli attuali cellulari sono in grado di operare su più cifre ().

  Cancellazione delle cifre
    Facciamo un altro esempio. Per calcolare (127·9721+0 .1234567-1234567)/3 posso battere:
127 [×] 9721 [+] 0 .1234567 [−] 1234567 [=] [ : ] 3 [=].
    Con una CT a 10 cifre ottengo 0 .041, con una a 12 ottengo 0 .0411533333333.
    Qual è il risultato migliore? Il risultato è esattamente 0 .041? o 0 .0411533333333 è il suo arrotondamento a 12 cifre?
    Se man mano guardo sul visore anche i risultati intermedi, osservo che 127·9721 fa 1234567; quindi il termine è equivalente a 0 .1234567/3, che vale 0 .0411522333…: nessuna delle due precedenti conclusioni è corretta!
    Il fenomeno che è all'origine di questo apparentemente strano comportamento viene chiamato "cancellazione delle cifre":
–  il risultato di 127·9721+0 .1234567, ossia 1234567.1234567, dalla CT a 10 cifre viene arrotondato a 1234567.123; nel calcolo della differenza tra 1234567.123 e 1234567, le cifre iniziali, uguali nei due numeri, si azzerano (1-1 fa 0, 2-2 fa 0, 3-3 fa 0, …), così che ottengo un valore 0 .123 con 3 sole cifre significative;
–  con la successiva divisone per 3 ottengo 0 .041, ma è illusorio considerarlo un risultato esatto in quanto è stato ottenuto dalla divisone di 0 .123, che era solo una approssimazione a 3 cifre.
    Analogamente, la CT a 12 cifre arrotonda 1234567.1234567 a 1234567.12345, nella differenza con 1234567 perde le cifre iniziali, calcola 0 .12345/3 e fornisce 0 .0411533333333; è illusorio considerarlo un arrotondamento corretto a 12 cifre in quanto è stato ottenuto dividendo un valore approssimato a 5 cifre.
    In realtà il fenomeno della "cancellazione delle cifre" (o, meglio, della perdita di cifre signficative) si verifica anche se i due numeri non hanno le stesse cifre iniziali, ma hanno comunque una differenza molto più piccola di loro, come nel caso di 999.98 e 1000 .01: se devo calcolare π(1000 .01-999.98) dove i due numeri sono valori approssimati, se con la CT ottengo 0 .09424778, è illusorio prendere 0 .094248 (arrotondamento a 5 cifre) come approssimazione del risultato in quanto il valore 0 .03 della differenza 1000 .01-999.98 ha 1 sola cifra significativa. Posso prendere solo 0 .09.
Nota. Le approssimazioni potrebbero essere fatte in modo più rigoroso utilizzando gli intervalli di indeterminazione ( calcolo approssimato). Ad esempio nell'ultimo caso:
- 1000 .01 sta per [1000 .005, 1000 .015]
- 999.98 sta per [999.975, 999.985]
- la loro differenza sta in [0 .02, 0 .04]
- il prodotto per π sta in [0 .06283…, 0 .1256…]
- quindi posso approssimare il risultato con [0 .062, 0 .126], o, meno precisamente, con [0 .06, 0 .13], o, meno precisamente, con 0 .09±0 .04.

    Con lo script "calcolo approssimato" (qui):

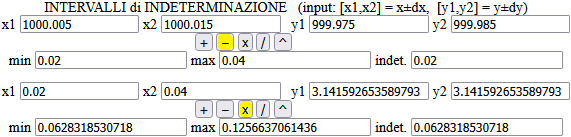
0.0942477796077 +/- 0.0314159265359

    Con "WolframAlpha" (vedi qui):

  I numeri macchina dei linguaggi di programmazione e di altre applicazioni

    Proviamo ad eseguire  843.27-843.23  e  5555.1251-5555  (che dovrebbero valere 0.04 e 0.1251)  con diversi mezzi di calcolo. Con JavaScript ottengo:

    Proviamo con la "piccolissima" calcolatrice presente qui:

ma, modificando il numero delle cifre a cui arrotondare il risultato:

    Analogamente, per 5555.1251-5555, otteniamo in un caso 0.1251, nell'altro 0.125100000000202

    Anche con "WolframAlpha", prima di premere [=], ottengo:

anche se dopo memorizza e visualizza il valore 0.04.

    Come mai accade ciò?
    A differenza di quanto avviene nelle usuali CT, che memorizzano i numeri in BCD, gran parte delle applicazioni per computer memorizzano i valori numerici nei registri associati alle variabili in forma binaria. Puoi rivedere come vengono trasformati in forma binaria i numeri qui. Ad ogni modo su ciò ritorniamo con una semplice applicazione a cui puoi accedere da qui.  Eccone due particolari uscite:

division of m by n with m < n (natural numbers in base ten) and result in a base of your choice By clicking  [one step]  you gradually get the figures of the result m = n = base =

division of m by n with m < n (natural numbers in base ten) and result in a base of your choice By clicking  [one step]  you gradually get the figures of the result m = n = base =

    Il concetto di numero limitato (cioè numero con periodo 0) dipende dalla base di rappresentazione. 1/2, che in base dieci è 0 .5, in base due diventa 0 .1; ma 1/10, che in base dieci diventa 0 .1, in base due diventa il numero illimitato 0 .00011001100110011… in quanto non riesco ad esprimere 0 .1 come somma di una quantità finita di frazioni prese tra 1/2, 1/4, 1/16, 1/32, ... (che, scritti in base due, diventano 0 .1, 0 .01, 0 .001, 0 .0001, …).
    A questo punto ci è facile capire le uscite strane considerate all'inizio del paragrafo:  843.27 e 843.23 vengono internamente espressi in forma binaria e approssimati, viene fatta la differenza tra questi due numeri in base 2, e il risultato viene visualizzato in base dieci: 0 .03999999999996362 è il risultato che differisce da 0 .04 del valore decimale corrispondente alle cifre binarie che si sono perse.

    I programmi considerati riescono a rappresentare un numero finito di numeri. Avranno, quindi, anche un numero massimo.
    Se con la "calcolatrice" presente qui calcoliamo 2¹⁰²⁴ otteniamo:

2 ^ 1024 = Infinity

    Otteniamo anche:

    L'uscita Infinity è la segnalato di un errore di overflow.
    Così come non riesco a rappresentare numeri troppo grossi, non riesco neanche a rappresentare numeri positivi troppo piccoli:

    Questo fenomeno si chiama underflow. Esso non viene segnalato dal computer. Sta all'utente interpretare opportunamente le uscite (e prestare attenzione nella messa a punto di programmi per l'esecuzione di alcuni algoritmi).

    Nei calcoli numerici WolframAlpha non si hanno queste limitazioni (sono presenti comunque quando lo si usa per rappresentazioni grafiche: vedi i commenti all'esempio in fondo alla pagina).

    Le calcolatrici incorporate negli attuali cellulari hanno meno limitazioni delle "normali" calcolatrici:  sono in grado di operare su una grande quantità di cifre e di approssimare molto meglio i risultati.  Hanno comunque anche esse sia overflow che underflow.  Ad esempio, facendo riferimento ad un particolare cellulare,  mentre 2^123456 fornisce 9.10216e37163   2^1234567 produce "non calcolabile",  mentre 2^-1234 fornisce 3.380534e-372   2^12345 produce 0.

    Un problema di calcolo si dice mal condizionato quando variando di poco i dati i risultati possono variare di molto. Ciò può dar luogo a valutazioni numeriche "sballate" non controllabili facilmente. Nei problemi più semplici questo in genere non accade, ma è bene tener presente questa possibilità.  Come esempio facciamo solo quello del calcolo di:
(A-1)*(A-2)*(A-3)*(A-4)*(A-5)*(A-6)*(A-7)*(A-8)*(A-9)*(A-10)*(A-11)*(A-12)*(A-13)*(A-14)*(A-15)*(A-16)*(A-17)*(A-18)*(A-19)*(A-20)
per A = 1.0000001 e per A = 1.0000005.  Con la "calcolatrice" già considerata ottengo nei due casi  -12164505732.334856  e  -60822442321.71447.  Si intuisce come in un calcolo che coinvolga un termine come questo non sia semplice tener conto degli errori di approssimazione legati alla precisione con cui si conosce il valore di A.  Lo stesso calcolo, con risultati analoghi, avremmo potuto farlo con WolframAlpha, mettendo il termine precedente seguito da "for A = 1.0000001" e da "for A = 1.0000005".

    I fogli di calcolo operano sui numeri in modo simile. Con opportune opzioni si può associare ad ogni cella un particolare tipo di visualizzazione (forma esponenziale o no, numero di cifre visualizzate, …). Ma, purtroppo, le versioni in italiano hanno una modalità di rappresentazione e visualizzazione dei numeri non compatibile con quelle degli altri paesi.

    Consideriamo un foglio di calcolo elettronico così impostato:

	A	B
1	=2000 .07-2000 .03	=(A1-0.04)*10^50
2	=2000.07-2000.03	=IF(A1=0.04;1;0)

["=IF(test;P;Q)" si comporta come "IF test THEN PRINT P ELSE PRINT Q"; in alcuni fogli di calcolo, a seconda delle opzioni scelte, viene usato "SE" al posto di "IF"]

    Se visualizziamo i valori, dando alla cella A2 l'opzione di rappresentare i numeri con 20 cifre, otteniamo:

	A	B
1	0.04	-3.64E36
2	0.03999999999996360000	0

o qualcosa di simile, con quasi tutti i tipi di foglio di calcolo.
    Anche per i fogli di calcolo 2000.07 - 2000.03 e 0.04 non sono uguali, anche se in apparenza, con i formati standard delle celle, il primo valore viene visualizzato sullo schermo come uguale al secondo. Comportamenti un po' "subdoli" come questo sono stati a volte fonte di errori nella gestione della contabilità mediante fogli elettronici da parte di alcune aziende.

    Si possono mettere a punto particolari programmi per visulizzare più cifre dei risultati, analoghi a quello visto sopra per la divisione tra interi. Esistono varie applicazioni matematiche che consentono di ottenere una quantità finita qualunque di cifre dei risultati di un certo calcolo.  Ma, tranne i casi in cui i risultati possono essere espressi come frazioni o in altri modi particolari (come radici quadrate di una frazione, per esempio), non esiste il modo di rappresentare esattamente il risultato di una operazione.  Comunque nei casi "pratici", in cui si opera con numeri approssimati, ciò non costituisce in genere un problema.

Esempio: qui         Esercizio   soluzione