Come viene effettuato il calcolo. Con una formula nota da vari millenni (almeno 3 secoli AC):
se indichiamo con A, B, C le lunghezze dei lati e con P il perimetro,
area = √( P·(P-2A)·(P-2B)·(P-2C) ) / 4 = √( (A+B+C)·(B+C-A)·(A+C-B)·(A+B-C) ) / 4
[ la formula è nota, impropriamente, come formula di Erone, vissuto circa 2 secoli DC ]

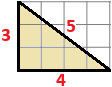
Verifichiamo la formula in un caso semplice,
Il triangolo a lato ha area 3·4/2 = 6. Con la formula di Erone:
√(12·2·6·4)/4 = √(24·24)/4 = 6 OK

L'area di un campo di forma poligonale misurando le distanze tra i vertici:

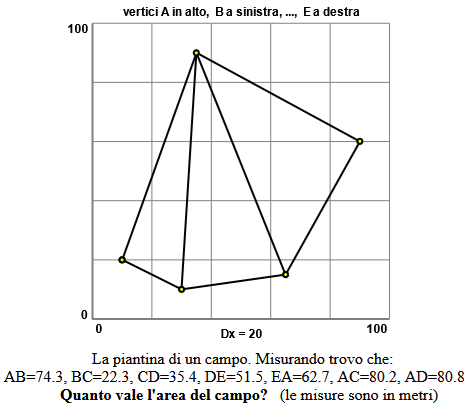
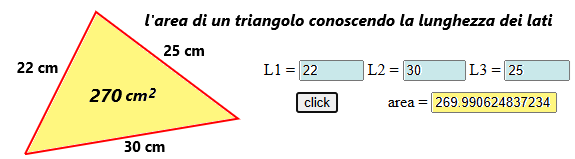
lati 74.3,22.3,80.2  area = 821.946110642298
lati 80.8,35.4,80.2  area = 1389.7812317051907
lati 80.8,51.5,67.2  area = 1722.9997507526662
1722.9997507526662+1389.7812317051907 = 3112.780982457857
3112.780982457857+821.946110642298 = 3934.727093100155

Arrotondo il risultato: area = 3935 m² Controlliamo con una stima:
il campo è poco meno della metà del quadrato, che ha area 100×100 = 10000 m²; 10000/2 = 5000; OK