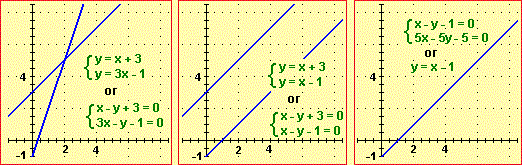

one solution no solution infinitely many solutions

• From an ancient Chinese book (Chiu-chang Suan-shu - 200 B.C.).
3 sheaves of a good crop, 2 sheaves of mediocre crop, and 1 sheaf of bad crop are sold for 39 dou.
2 sheaves of good, 3 mediocre, and 1 bad are sold for 34 dou.
1 good, 2 mediocre and 3 bad are sold for 26 dou.
What is the price received for each sheaf of a good crop, each sheaf of a mediocre crop, and each sheaf of a bad crop?
Today this problem can be formulated as 3 equations in 3 unknowns, where x, y, and z represent the price of a good, mediocre, and bad crop, respectively:

• I have Lemon Rum with an alcohol content of 30% and Rum with an alcohol content of 40%. I want to get 300 ml of cocktail with an alcoholic strength of 25% by adding equal quantities of Lemon Rum and Rum to orange juice. How much should I take from each of the three ingredients?
Let x, y, and z be the quantities (in ml) of Lemon Rum, Rum and orange juice.
x+y+z = 300 (300 ml of cocktail); x−y = 0 (equal quantities of Lemon Rum and Rum); 30%·x + 40%·y = 25%·300
(Lemon Rum with 30% of alcohl, Rum with 40% of alcohl → 300 ml with 25% of alcohl).
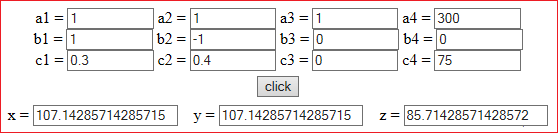
107 ml of Lemon Rum and Rum, 86 ml of orange juice.
[se vuoi esprimere i risultati sotto forma di frazione puoi usare lo script "frazioni":
107/1 + 142857/999999 → 750/7 85/1 + 714285/999999 → 600/7 ]
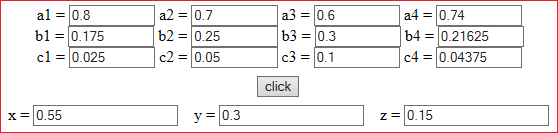
• I have three bars made up of silver, copper and tin. Their compositions are:
silver copper tin 1^ 80% 17.5% 2.5% 2^ 70% 25% 5% 3^ 60% 30% 10%
How much metal does it take from each bar to get a metal composed in the following way?
silver: 74%, copper: 21.625%, tin: 4.375%
Let x, y and z be the fractions that must be taken from each bar.
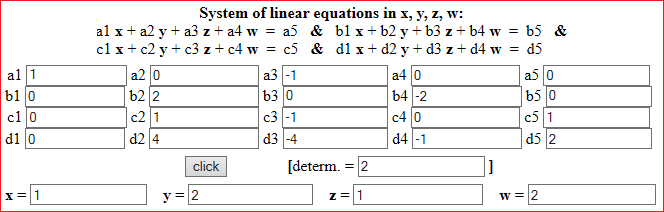
• To have equilibrium in a certain structure, the parameters x, y, z, w must satisfy the following equations. Find the values of x, y, z, w (problem from D.R.Green, J.Lewis - "Science with Pocket Calculators").
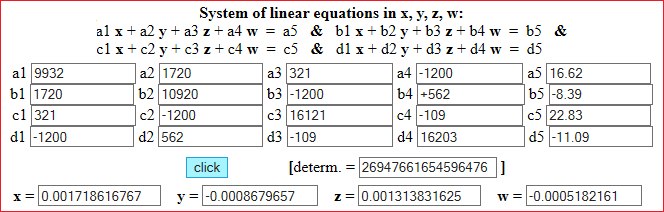
Rounding: x = 1.719·10−3, y = 8.680·10−4, z = 1.314·10−3, w = 5.182·10−4
• Find x, y, z, w integers such that
Looking at the elements that appear on the two sides of the relationship, we have that it must be (for, in order, Cu, H, S, O):
Cu: x - z = 0 H: 2y - 2w = 0 S: y - z = 1 O: 4y - 4z - w = 2
Cu + 2H2SO4 → CuSO4+ 2H2O + SO2