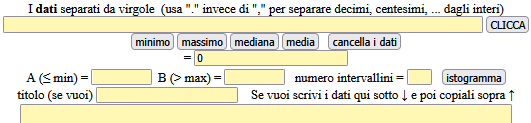
Metti i dati nella prima casella.  Se un dato, ad es. 7, si ripete ad es. 3 volte puoi introdurre 7,7,7 oppure 7*3.  Premi [CLICCA] e i tasti di cui ti interessano i corrispondenti valori.  Scegli l'intervallo [A,B] e il numero di intervalli con cui vuoi costruire l'istogramma (tieni presente che se ad es. A=5 e B=13 e vuoi intervalli ampi 1 devi prendere 13-5=8 intervallini).

Pesi (arrotondati ai chilogrammi) di un gruppo di ragazzi 13-enni    (altri dati)

64, 66, 73, 86, 70, 75, 68, 86, 88, 63, 73, 70, 69, 66, 77, 80, 80, 77, 82, 61, 77, 71, 59, 84, 86, 70, 77, 70, 97, 68, 66, 70, 70, 68, 70, 68, 81, 73, 61, 73, 59, 70, 68, 67, 70, 68, 64, 82, 86, 66, 68, 74, 64, 64, 62, 56, 70

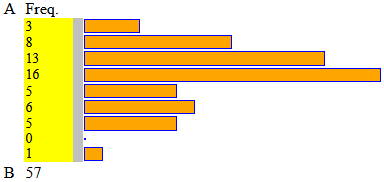A = 55 B = 100   intervalli = 9   di ampiezza 5  -  pesi maschi 13-enni
n = 57   min = 56 max = 97   mediana = 70   1^|3^ quarto = 66|77   media = 71.7719298245614
percentuali:
| 5.26 | 14.04 | 22.81 | 28.07 | 8.77 | 10.53 | 8.77 | 0 | 1.75 |
corrispondenti alle frequenze:
3+8+13+16+5+6+5+0+1

Le lunghezze di una grande quantità di (semi di) fave studiati da una classe di ragazzi dodicenni

fave - lunghezza (cm):
 1.35, 1.65, 1.80, 1.40, 1.65, 1.80, 1.40, 1.65, 1.85, 1.40, 1.65, 1.85, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 2.25, 1.55, 1.70, 1.55, 1.70, 1.55, 1.70, 1.60, 1.70, 1.60, 1.75, 1.60, 1.75, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.00, 1.55, 1.70, 1.75, 1.30, 1.55, 1.70, 1.75, 1.40, 1.60, 1.70, 1.75, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.45, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.75, 1.90, 1.50, 1.60, 1.75, 1.90, 1.50, 1.65, 1.75, 1.90, 1.55, 1.65, 1.75, 1.95, 1.55, 1.65, 1.75, 2.00, 1.55, 1.65, 1.75, 2.30, 1.35, 1.65, 1.80, 1.40, 1.65, 1.80, 1.40, 1.65, 1.85, 1.40, 1.65, 1.85, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.65, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 1.90, 1.50, 1.70, 2.25, 1.55, 1.70, 1.55, 1.70, 1.55, 1.70, 1.60, 1.70, 1.60, 1.75, 1.60, 1.75, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.60, 1.80, 1.00, 1.55, 1.70, 1.75, 1.30, 1.55, 1.70, 1.75, 1.40, 1.60, 1.70, 1.75, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.40, 1.60, 1.70, 1.80, 1.45, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.80, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.70, 1.85, 1.50, 1.60, 1.75, 1.90, 1.50, 1.60, 1.75, 1.90, 1.50, 1.65, 1.75, 1.90, 1.55, 1.65, 1.75, 1.95, 1.55, 1.65, 1.75, 2.00, 1.55, 1.65, 1.75, 2.30

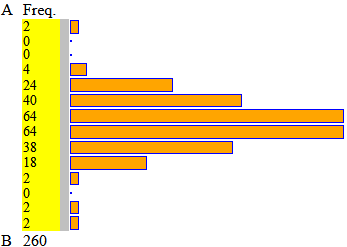
A = 1 B = 2.4   intervalli = 14 di ampiezza 0.1 - lughezza fave
n = 260   min = 1 max = 2.3   mediana = 1.65   1^|3^ quarto = 1.55|1.75   media = 1.6592307692308
percentuali:
| 0.77 | 0 | 0 | 1.54 | 9.23 | 15.38 | 24.62 | 24.62 | 14.62 | 6.92 | 0.77 | 0 | 0.77 | 0.77 |

In alternativa si possono prima ordinare i numeri (con lo script "ordina"), contare quanti sono per ogni uscita e ...

1, 1, 1.3, 1.3, 1.35, 1.35, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.45, 1.45, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.55, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.6, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.65, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.7, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.8, 1.85, 1.85, 1.85, 1.85, 1.85, 1.85, 1.85, 1.85, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.9, 1.95, 1.95, 2, 2, 2.25, 2.25, 2.3, 2.3

... introdurre:
1*2, 1.3*2, 1.35*2, 1.4*22, 1.45*2, 1.5*24, 1.55*16, 1.6*42, 1.65*22, 1.7*42, 1.75*22, 1.8*30, 1.85*8, 1.9*16, 1.95*2, 2*2, 2.25*2, 2.3*2

Voglio avere un'idea di come sono distribuiti i pesi delle fave.
Posso ritenere che siano proporzionali ai loro volumi, che posso stimare facendo il cubo delle lunghezze. Per fare ciò introduco i dati precedenti nello script "calcolatrice":

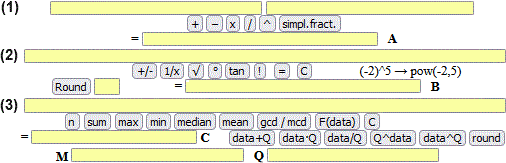
Metto la riga precedente in (3), metto 3 in Q e clicco [data^Q]. Ottengo:
1*2, 2.1970000000000005*2, 2.4603750000000004*2, ...
Per arrotondare (ad es. a 5 cifre dopo ".") i dati, ricopio queste uscite in (3), metto 5 a destra di [Round] e clicco [round]. Ottengo:

1*2, 2.197*2, 2.46038*2, 2.744*22, 3.04863*2, 3.375*24, 3.72388*16, 4.096*42, 4.49212*22, 4.913*42, 5.35938*22, 5.832*30, 6.33163*8, 6.859*16, 7.41488*2, 8*2, 11.39063*2, 12.167*2

Con il nostro script ottengo:

Come si vede, mentre l'istogramma delle lunghezze aveva un andamento simmetrico, a forma di "campana", quello dei loro volumi e dei loro pesi non lo ha (come abbiamo visto, e rivedremo, accade anche per i pesi delle persone). Sono pochi i fenomeni a cui corrisponde un andamento "a campana".

Un esempio di come rappresentare dadi già classificati in intervalli di uguale ampiezza

Deaths per 10000 inhabitants per age group / morti ogni 10000 abitanti per fascia di età (Italy, 2006).

[0,5) 43       [5,10) 5      [10,15) 6     [15,20) 16
[20,25) 23     [25,30) 26    [30,35) 28    [35,40) 37
[40,45) 56     [45,50) 88    [50,55) 141   [55,60) 225
[60,65) 350    [65,70) 518   [70,75) 814   [75,80) 1245
[80,85) 1771   [85,90) 2027  [90,95) 1643  [95,100) 727
[100,105) 195  [105,110) 17
                             10001 data in 22 intervals

La somma non è 10000, a causa degli arrotondamenti (nelle pubblicazioni in cui le tabelle contenenti delle distribuzioni percentuali hanno la somma delle percentuali uguale sempre a 100  le percentuali non sono state arrotondate correttamente: è stato usato qualche trucco, non svelato ai lettori, per - diseducativamente - non creare loro imbarazzi!  un semplice esempio: se A=10, B=10 e C=10, la distribuzione percentuale - 33, 33 e 33, o 33.3, 33.3 e 33.3, o ... - non può avere come somma 100).

Scelgo come "A" il primo estremo dell'intervallo iniziale e come "B" il secondo estremo dell'intervallo finale.  Il "numero degli intervalli" coincide con il numero delle frequenze introdotte.  Potrei anche scegliere come "numero degli intervalli" un divisore del numero, nel nostro caso invece di 22 potrei scegliere 11 o 2.

Classified data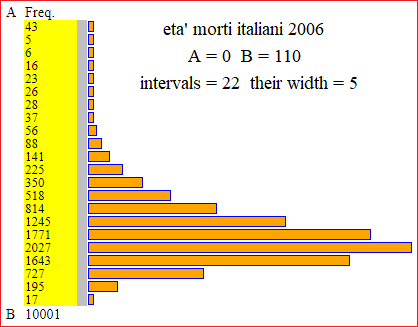 

A = 0   B = 110   intervalli = 22 di ampiezza 5
n = 10001  min = 2.5 max = 107.5  mediana = 82.5 1^|3^ quarto = 77.5|92.5  media = 81.13363663633636
2.5*43, 7.5*5, 12.5*6, 17.5*16, 22.5*23, 27.5*26, 32.5*28, 37.5*37, 42.5*56, 47.5*88, 52.5*141, 57.5*225, 62.5*350, 67.5*518, 72.5*814, 77.5*1245, 82.5*1771, 87.5*2027, 92.5*1643, 97.5*727, 102.5*195, 107.5*17
percentuali: | 0.43 | 0.05 | 0.06 | 0.16 | 0.23 | 0.26 | 0.28 | 0.37 | 0.56 | 0.88 | 1.41 | 2.25 | 3.5 | 5.18 | 8.14 | 12.45 | 17.71 | 20.27 | 16.43 | 7.27 | 1.95 | 0.17 |

Con 11 intervalli 3
con 2 intervalli		 

Human body height and weight (altezza e peso corporeo); 4170 Italian males in their twenties, in the year 1990.   (here and here)

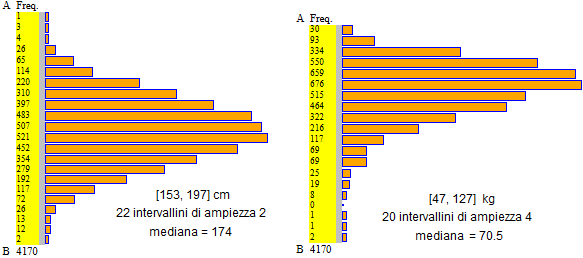
Abbiamo suddiviso gli intervalli in modo che gli intervallini avessero ampiezza intera.  I dati dei pesi inseriti nel file sono 62.5, 64.5, 70.5, 55.5, ... in quanto i pesi letti sulle bilance (62, 64, 70, 55, ...) erano troncati: abbiamo aggiunto 0.5 in modo da avere dati centrati negli intervallini.

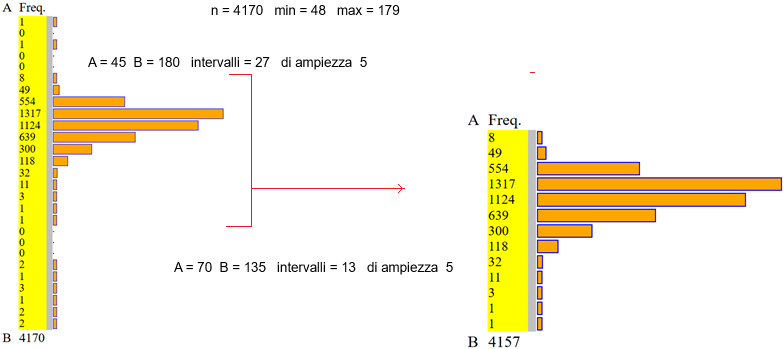
NOTA. Possiamo anche tracciare l'istogramma escludendo dei dati iniziali e/o finali. Ad esempio nel caso del perimetro toracico dei 4170 maschi di cui sopra, recuperabile here, otterremmo l'istogramma sotto a sinistra (probabilmente nel file originale c'erano dei dati mal registrati o mal trascritti), mentre, escludendo una decina di dati, scegliendo A e B compresi tra min e max, possiamo ottenere l'istogramma a destra:

La distribuzione percentuale per età dei laureati dell'università di Genova nel triennio 1984-1986 (campione di 1233 laureati su un totale di 6392), da un'indagine condotta dall'IRES-Liguria (Istituto Ricerche Economiche e Sociali):

22232425262728293031323334353637383940
0.40.86.713.119.418.414.395.53.11.91.61.61.21.10.50.50.50.4

Le età sono (ovviamente) troncate agli interi. Per avere il calcolo corretto dei valori medi aggiungo 0.5 alle età. Per avere dati interi moltiplico le frequenze percentuali per 10:

22.5*4, 23.5*8, 24.5*67, 25.5*131, 26.5*194, 27.5*184, 28.5*143, 29.5*90, 30.5*55, 31.5*31, 32.5*19, 33.5*16, 34.5*16, 35.5*12, 36.5*11, 37.5*5, 38.5*5, 39.5*5, 40.5*4

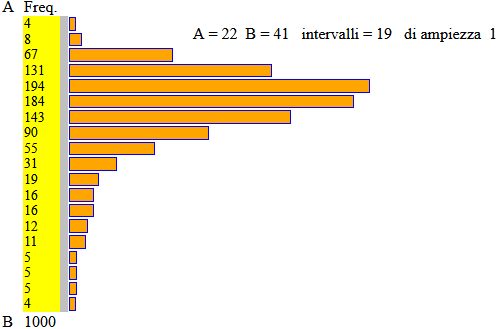
n. dati = 1000       n. input = 19
minimo = 22.5      massimo = 40.5
mediana = 27.5      media = 28.118
1^ quartile: 26.5      3^ quartile: 29.5

Gli istogrammi possono essere "sintetizzati" anche con i box-plot (vedi qui "box-plot cl", boxplot di dati classificati):

 



 

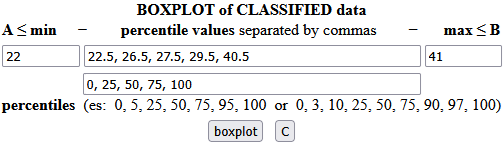
Posso utilizzare anche direttamente i box-plot (vedi qui "box-plot"). Introducendo:

22.5*4, 23.5*8, 24.5*67, 25.5*131, 26.5*194, 27.5*184, 28.5*143, 29.5*90, 30.5*55, 31.5*31, 32.5*19, 33.5*16, 34.5*16, 35.5*12, 36.5*11, 37.5*5, 38.5*5, 39.5*5, 40.5*4

ottengo:

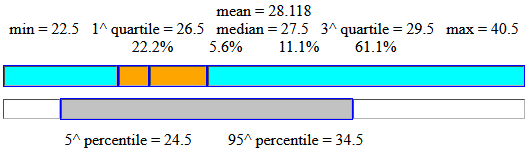
che mi dà più informazioni.

Zombies
A 1 long wall; a W wide hole in the wall; every second a zombie arrives in a completely random position of the wall.  Let W be 1/10; let's simulate 1 hour.  The distribution (in 5 sec intervals) of the waiting times between a pass through the hole of a zombie and the next pass.
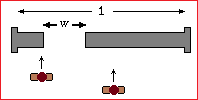[the histogram tends to have the graph of  x → W·exp(-W·x)  as profile]
  

17, 10, 8, 36, 7, 21, 1, 6, 2, 8, 3, 5, 7, 3, 7, 2, 2, 6, 2, 15, 12, 10, 2, 18, 1, 19, 14, 22, 6, 2, 2, 7, 4, 8, 12, 6, 12, 2, 17, 4, 1, 3, 5, 15, 11, 1, 4, 16, 6, 11, 6, 20, 2, 14, 1, 15, 38, 1, 7, 23, 10, 4, 25, 1, 1, 4, 11, 7, 1, 4, 2, 6, 7, 15, 4, 20, 17, 3, 15, 8, 16, 2, 15, 3, 3, 3, 30, 13, 23, 19, 38, 18, 4, 17, 1, 1, 1, 21, 5, 45, 11, 3, 5, 2, 19, 9, 5, 16, 5, 1, 1, 35, 12, 6, 22, 29, 16, 13, 8, 9, 12, 4, 4, 1, 10, 1, 2, 10, 22, 2, 2, 16, 20, 12, 5, 5, 2, 12, 1, 9, 1, 26, 37, 1, 6, 2, 8, 7, 6, 1, 5, 8, 6, 6, 19, 4, 23, 12, 33, 4, 3, 8, 4, 2, 28, 20, 10, 15, 15, 4, 5, 2, 3, 1, 1, 18, 4, 2, 15, 10, 6, 1, 9, 5, 32, 1, 31, 20, 10, 5, 23, 1, 9, 11, 3, 20, 14, 5, 5, 5, 1, 18, 3, 23, 7, 10, 10, 14, 3, 8, 9, 3, 8, 1, 21, 3, 5, 2, 31, 1, 31, 1, 3, 37, 5, 7, 4, 21, 7, 7, 2, 13, 4, 4, 1, 1, 8, 25, 18, 4, 5, 6, 14, 17, 2, 11, 6, 5, 6, 8, 1, 9, 1, 6, 9, 4, 1, 5, 1, 14, 6, 12, 3, 3, 7, 6, 3, 10, 31, 3, 3, 4, 8, 4, 12, 5, 1, 3, 1, 18, 25, 6, 24, 14, 2, 1, 29, 23, 31, 15, 24, 2, 2, 5, 4, 5, 15, 3, 3, 14, 11, 5, 2, 9, 45, 3, 4, 4, 21, 9, 16, 4, 12, 17, 12, 4, 14, 3, 4, 20, 5, 8, 8, 6, 21, 19, 4, 5, 5, 5, 28, 18, 9, 10, 3, 12, 2, 2, 4, 15, 2, 7, 3, 4, 8, 6, 10, 14, 7, 14, 13, 9, 4, 5, 12, 1, 3, 4, 14, 8, 1, 6, 3, 16, 1, 6, 9, 2, 3, 6, 21, 15, 2, 20, 18, 9, 7, 3, 5, 7, 18

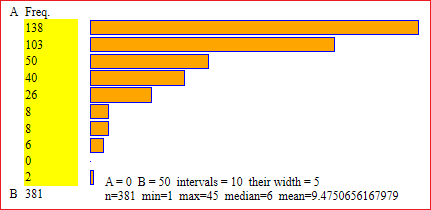
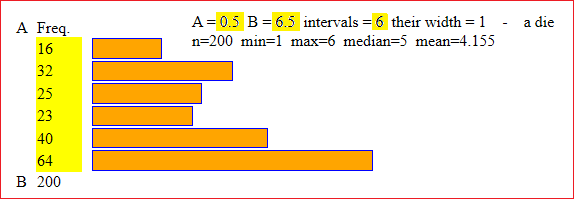
The study of the cast of a die made of thin cardboard:
                                                                             
5,5,4,3,3,1,6,2,5,6,2,5,3,6,5,6,3,2,1,6, 1,6,6,3,5,2,1,5,2,5,5,3,6,6,4,6,6,5,6,2, 1,6,6,3,2,2,5,6,3,2,6,6,6,4,2,3,6,6,6,2, 6,4,5,4,6,2,3,5,6,6,2,2,1,5,5,3,5,3,5,6, 2,1,4,3,6,6,6,4,3,4,6,6,4,5,4,4,2,2,6,4, 4,6,2,5,3,6,6,3,3,2,2,6,1,4,6,5,3,3,4,1, 6,4,6,6,2,5,5,1,5,2,6,5,2,2,4,1,2,2,6,1, 6,5,5,6,1,3,3,4,5,5,5,6,4,4,6,3,6,3,6,6, 4,2,6,6,6,1,4,5,6,5,6,5,5,5,6,6,2,1,6,3, 6,6,5,3,5,2,2,4,6,6,5,2,5,5,6,6,5,2,6,1