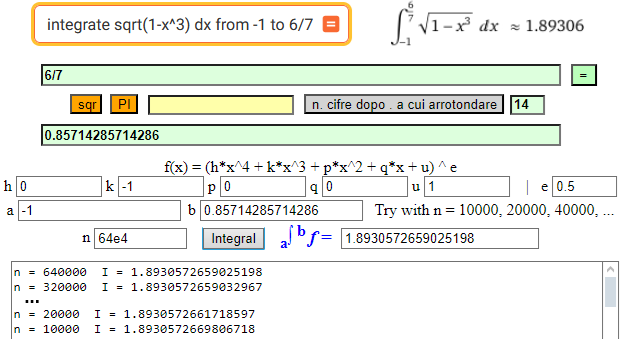
Per calcolare con questo script l'integrale tra -1 e 6/7 di √(1-x³) calcolo prima il valore numerico di 6/7 con la calcolatrice (0.85714285714286 arrotondando a 14 cifre dopo il punto).  Ecco il valore dell'integrale che si può ottenere con WolframAlpha e poi quello ottenibile con lo script.

Fermandomi qui posso prendere l'arrotondamento 1.89305726590.

Per calcolare con questo script l'integrale di √(1-x³) tra -1 e ³√(6/7) posso calcolare la radice cubica usando la funzione cbrt (cube root): vedi l'help della "calcolatrice".

[0.94991425159300 è l'arrotondamento a 14 cifre]

Poi integrando con questo script tra -1 e 0.949914251593:
    n = 640000   I = 1.9400079539697368
    n = 320000   I = 1.9400079539727484
      ...
    n = 20000   I = 1.9400079549670644
    n = 10000   I = 1.9400079579617122

Posso prendere 1.94000795397.  WolframAlpha con integrate sqrt(1-x^3) form -1 to (6/7)^(1/3) avrebbe fornito l'arrotondamento 1.94001.

Se volessi valutare con più precisione l'integrale potrei usare un programmino in JavaScript: vedi