VEDI

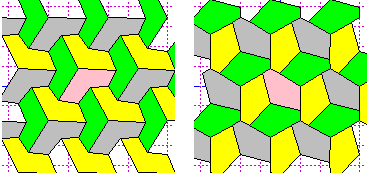
Le tassellazioni (o pavimentazioni) di Escher

Non è facile capire come costruire tassellazioni che non siano realizzate con poligoni regolari. Una risposta a questo problema è data dal seguente teorema (dovuto al cristallografo Friedrich Haag), utlizzato dall'artista Maurits Cornelis Escher (vedi) e spesso chiamato "teorema di Escher":

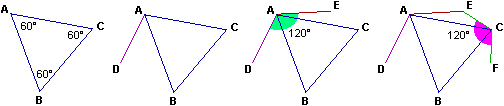
Dal vertice A di un triangolo equilatero ABC si tracci un segmento AD di lunghezza e direzione arbitrarie (AD potrebbe, per esempio, anche essere più lungo di AB e/o secare BC); poi si tracci il segmento AE tale che AE=AD e ∠DAE=120°.  Si tracci EC; poi si tracci il segmento CF tale che EC=CF e ∠ECF=120°.  Infine si congiungano F con B e B con D.

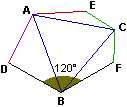
Si ha che: DB=BF e ∠FBD=120°, e che il piano è completamente riempibile senza sovrapposizioni da esagoni uguali ad ADBECF.

Per approfondimenti si vedano The Mathematical Side of M. C. Escher di D. Schattschneider e Napoleon, Escher and Tessellations di J.F. Riflby.

Per altri tipi di tassellazioni vedi qui