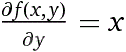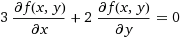0. I Premessa

    Abbiamo visto come, data una funzione, se ne può studiare la variazione utilizzando le sue derivate prima, seconda, ….  In questa scheda vedremo, viceversa, che da informazioni su come varia una funzione si possono dedurre informazioni sulla funzione stessa.  Il primo paragrafo illustra in breve il contenuto della scheda e, in gran parte delle scuole, è sufficiente per avere un'idea di che cosa siano, a che cosa servano e come si studino i "modelli differenziali".  I paragrafi successivi sono di approfondimento, per alcuni tipi di scuole.

1. I primi modelli differenziali

    Suppongo di sapere che un corpo A si muove alla velocità costante di 8 m/s.  Indico con t il tempo espresso in secondi dall'istante (t = 0) in cui l'oggetto è partito.  Sto ipotizzando, per semplicità, che un corpo possa partire immediatamente a tale velocità; in realtà sappiamo che la potrà raggiungere solo dopo qualche istante.  Indico con x_A la strada in metri percorsa dall'oggetto dopo t secondi.  La sua velocità sarà la derivata  d x_A / dt, che posso indicare anche aggiungendo un apice ad x_A, come è fatto nel grafico sottostante.

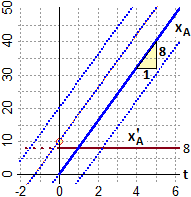
So che d xA / dt = 8.  Posso dedurre che xA = 8·t, come appare anche sul grafico.  Ma questa soluzione corrisponde al fatto che xA(0) = 0, mentre non avevo alcuna informazione sulla posizione di partenza del corpo.     Potrebbe essere anche che xA(0) = 10 (vedi il punto cerchiato) o xA(0) = 20, a cui corrisponderebbero le equazioni xA = 8·t+10 o xA = 8·t+20.  Sul grafico, oltre a queste, è rappresentata la soluzione xA = 8·t−10.  Sono tutte rette parallele.  Le parti a sinistra dell'asse y corrispondono al movimento del corpo nel caso in cui fosse partito prima dell'istante t = 0.

    Suppongo, ora, di sapere che un corpo B si muove alla velocità crescente di (3·t + 1.5) m/s, dove t è il tempo espresso in secondi dall'istante in cui l'oggetto è partito.  Indico con x_B la strada in metri percorsa dall'oggetto dopo t secondi.  Il grafico di come varia la velocità è rappresentato a sinistra:

   

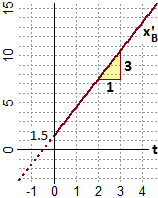
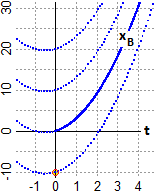
    Dunque d x_B / dt = 3·t + 1.5.  Posso dedurre che  x_B = 3/2·t² + 1.5 t. Ma, anche in questo caso, è una soluzione (rappresentata sopra a destra) che corrisponde al fatto che x_B(0) = 0, mentre non avevamo alcuna informazione sulla posizione di partenza del corpo.  Potrebbe essere anche che, ad esempio, x_B(0) = 10, x_B(0) = 20 o x_B(0) = −10 (vedi il punto cerchiato), a cui corrispondono le altre curve rappresentate sul grafico (x_B = 1.5·t² + 1.5 t + c con c pari a 10, 20 o − 10).

    Se astraggo dal contesto, posso tradurre alcuni dei problemi visti sopra in questi modi:

(1)  So che f '(x) = 8.  (a) Che cosa posso dedurre su f?  (b) E se, ad es., so che f(0) = 10?
    (a) Che f è del tipo f(x) = 8·x + c.  (b)  8·0+c = 10, quindi c=10 e  f(x) = 8·x+10.
(2)  So che f '(x) = 3x+3/2.  (a) Che cosa posso dedurre su f?  (b) E se, ad es., so che f(0) = −10?
    (a) Che f è del tipo f(x) = 3/2·x² + 3/2 x + c.  (b)  3/2·0+3/2·0+c = −10, quindi c=−10 e  f(x) = 3/2·x² + 3/2 x − 10.

    Consideriamo un'altra situazione.  Un'automobile C all'istante t è nella posizione x_C(t), dove t è espresso in secondi. Indichiamo questa posizione, espressa in metri, più semplicemente con s(t) (dove s sta per "strada" o "spazio").  Supponiamo che l'auto sia in accelerazione costante, e che questa sia s"(t) = 5, in m/s².  Ovviamente questo accadrà in un breve intervallo di tempo: l'automobile ha una velocità limite oltre cui non può andare.  Che cosa posso concludere sul valore di s(t)?
    Conoscendo l'accelerazione posso dedurre qualche informazione sulla velocità:  s'(t) potrebbe essere  5·t  o  5·t+5  o  5·t−3  o, in generale,  5·t + h.
    Se s'(t) = 5·t potrei dedurre (come fatto sopra per x_B) che s(t) = 2.5·t² + k.
    In generale, se s'(t) = 5·t + h posso dedurre che s(t) = 2.5·t² + h t + k

    Da che cosa dipendono i valori di h e di k?  Pensiamo, prima, al problema.  Conosco l'accelerazione dell'auto.  La sua posizione al variare del tempo da che cosa dipende?  Sicuramente dalla posizione iniziale, cioè s(0).  E dalla velocità iniziale, cioè s'(0).  Dipende, quindi, da due valori.  Vediamo la cosa dal punto di vista matematico.

    Astraendo dal contesto posso descrivere il problema così:

(3)  So che f "(x) = 5.  (a) Cosa posso dedurre su f '?  (b) e su f ?  (c) E se, ad es., so che f '(0) = 1 e che f(0) = 2?

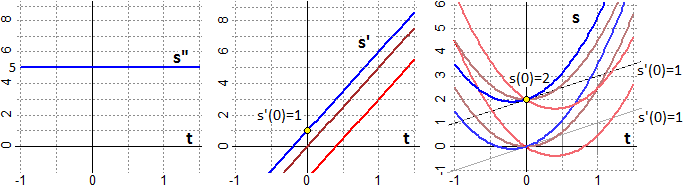
    Da  s"(t) = 5  posso ricavare che  s'(t) = 5·t + h.  Vedi la figura soprastante a sinistra.
    Deduco che s' in funzione di t ha il grafico di una retta con pendenza 5.  Vedi la figura al centro.  So che s'(0)=1; posso quindi individuare una particolare espressione di s':  da s'(0) = 5·0 + h = 1 ricavo che h = 1.  Nella figura la s' soluzione è in colore blu.
    Da  s'(t) = 5·t + h  ricavo  s(t) = 2.5·t² + h·t + k.  Sopra a destra sono rappresentate diverse di queste curve.  Ne sono evidenziate, in blu, due che corrispondono a s'(0) = 1, ossia a h = 1.  Se so che s(0)=2 ne indivuo una sola: da s(t) = 2.5·t² + t + k ottengo 2.5·0² + 0 + k = 2, da cui k = 2;  la soluzione è  s(t) = 2.5·t² + t + 2.

    Equazioni come f '(x) = 8, f '(x) = 3x+3/2 e f "(x) = 5, in cui l'incognita è una funzione (f) che compare sotto un simbolo di derivazione (derivata prima o seconda o …) vengono chiamate equazioni differenziali (ricordiamo che la derivata viene chiamata anche coefficiente differenziale).  Come abbiamo visto una equazione differenziale ha infinite soluzioni.  Per avere un'unica soluzione dobbiamo affiancare alla equazione delle condizioni sui valori che essa, e le sue derivate successive, assumono in alcuni punti.  Un'equazione differenziale affiancata da indicazioni di questo tipo viene chiamata modello differenziale.

    Ad esempio  s"(t) = 5, s'(0) = 1, s(0) = 2,  ossia l'equazione differenziale s"(t) = 5 assieme alle condizioni s'(0) = 1 e s(0) = 2,  costituiscono un modello differenziale che ha come soluzione s(t) = 2.5·t² + t + 2.

Un altro esempio.  Quali sono le funzioni che hanno come derivata sé stesse?  A questo problema corrisponde il modello differenziale  f '(x) = f(x).  Noi sappiamo che una soluzione di questa equazione è  f = exp.  Infatti D(exp) = exp.  Ma, ricordando che, se k è una costante numerica, D(k·f) = k·D(f), capiamo che sono soluzioni anche tutte le funzioni f(x) = k·exp(x);  infatti Dx(k·exp(x)) = k·Dx(exp(x)) = k·exp(x).     A destra sono rappresentate alcune funzioni di questo tipo.  In blu è rappresentata la soluzione dell'equazione differenziale che si ottiene imponendo la condizione  f(1) = 4.  Quanto vale k?  Da k·exp(1) = 4 ottengo k = 4/exp(1) = 4/e = 1.471….  Potrei anche esprimere la soluzione come f(x) = 4·exp(x−1).  Infatti  4/exp(1)·exp(x) = 4·exp(x)/exp(1) = 4·exp(x−1).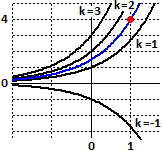

    Anche molti modelli differenziali possono essere risolti utilizzando WolframAlpha. Ad esempio nei casi precedenti basta che metta come input, rispettivamente,   s"(t)=5, s'(0)=1, s(0)=2   e   f'(x)=f(x), f(1)=4.
    Posso anche trovare valori particolari senza copiare e mettere in input la soluzione, con, ad esempio:  s"(t)=5, s'(0)=1, s(0)=2, what s(1)?   e   s"(t)=5, s'(0)=1, s(0)=2, what s(7)?.

    Abbiamo già incontrato, negli anni scorsi, delle equazioni differenziali?  Se ci ripensiamo, la antiderivata o primitiva di una funzione F non è altro che una soluzione G dell'equazione differenziale  G'(x) = F(x), che abbiamo espresso poi anche come integrale indefinito di F:  ∫ F(x) dx.

    Invece di scrivere  ∫ 6x dx = 3x² + c  si può dire, in modo alternativo (e più corretto), che l'equazione differenziale  y'(x) = 6x  ha come soluzioni tutte le funzioni  y(x) = 3x² + c  al variare di c in R.

    Qualche breve considerazione storica.  Lo studio delle prime equazioni differenziali risale alla fine del XVII secolo, quando, da Newton e Leibniz, venne individuato il teorema fondamentale dell'analisi, che ha messo in relazione la derivazione e l'integrazione.  Emerse, presto, il problema che, a differenza della derivazione, per la quale esiste un procedimento standard per associare ad una funzione la sua funzione derivata, non c'è una tecnica standard per associare ad una funzione le sue antiderivate. Si deve arrivare al XVIII secolo per la messa a punto di tecniche specifiche per la risoluzione di varie classi di equazioni differenziali e per la dimostrazione di alcuni teoremi che assicurano l'esistenza delle soluzioni di equazioni differenziali che soddisfano certe condizioni generali. Di questi aspetti ti occuperari se proseguirai gli studi in ambito matematico o fisico.  Qualche approfondimento sui modelli differenziali lo puoi trovare nei prossimi paragrafi.

2. Equazioni differenziali del 1º ordine

    L'equazione differenziale  s"(t) = 5,  così come l'equazione differenziale  s"(t) + 3·s'(t) − t = 5,  sono chiamate del secondo ordine in quanto la derivata di massimo grado di s che compare in esse è quella di secondo grado.  Invece  (a)  s'(t) = 3t + 3/2  e  (b)  f '(x) = f(x)  sono equazioni differenziali del primo ordine in quanto in esse al pi compare la derivata prima (di s e di f).
    Soffermiamoci sulle equazioni differenziali del 1º ordine.  Esse in generale sono delle equazioni in cui, indicata con F la funzione incognita e con x la variabile di input, compare F ' e possono comparire, oltre ad x, sia F stessa che vari simboli di funzione e di costante.  Due esempi, in aggiunta ai precedenti:

(c)  sale'(t) = 0.01 − sale(t)/100           (d)  y'(x) = x − y(x)

    Sotto sono rappresentati i campi direzionali (o campi di pendenza, slope fields in inglese) associati alle equazioni differenziali precedenti: data un'equazione y'(x) = g(x,y) il campo direzionale ne raffigura le possibili soluzioni rappresentando per una grande quantit di punti (x,y) un segmentino centrato nel punto e con la pendenza indicata dalla equazione, ossia g(x,y).

    Nel caso (a) sono tutte le funzioni t → 3/2·t² + 3/2·t + k.  Nella figura è evidenziata la particolare soluzione che in 0 vale −10, che come abbiamo visto corrisponde a k = −10.  Nel caso (b) sono tutte le funzioni x → k·exp(x) .  Nella figura sono evidenziate la soluzione che in 1 vale 4 e quella che in 1/2 vale −2.  Anche in questo caso abbiamo visto come si può risalire al valore di k nei vari casi.

(a)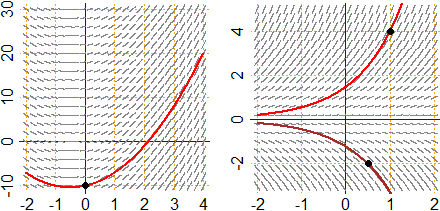

(b)

    Consideriamo il caso (c).  Esso corrisponde al seguente problema.

    Un recipiente contiene 100 litri di una soluzione contenente 5 kg di sali.  Viene fatta entrare, con la portata di 1 litro/min, un'altra soluzione con una concentrazione di sali di 10 g/litro.  Il livello è mantenuto costante mediante un'opportuna valvola.  Supponiamo che la portata sia costante e che il liquido sia costantemente mescolato.
    Quanto sale rimane nel recipiente dopo un'ora?

    Indichiamo con  sale(t)  il sale in kg presente al minuto t-esimo.  Quindi sale(t)/100 è la concentrazione di sale (in kg per litro) nello stesso istante.  Inzialmente la concentrazione è sale(0)/100 = 0.05 ma essa via via cala in quanto viene introdotto liquido con concentrazione di 10 g (ossia 0.01 kg) di sali per litro, ossia (esprimendosi in kg per litro) 0.01.
    Il flusso di sale in entrata è dunque  0.01 kg/litro·1 litro/min = 0.01 kg/min, ossia 0.01 esprimendosi in kg al minuto.  Il liquido esce con la stessa velocità con cui entra (1 litro/min) ma, riducendosi la concentrazione di sale, con un flusso di sale che via via si riduce:  il flusso di sale in uscita è  "concentrazione di sale" · "1 litro al minuto",  ossia sale(t)/100·1 = sale(t)/100.
    Riassumendo all'inizio  sale(0) = 5;  poi  il flusso di sale è  0.01 − sale(t)/100.  Utilizzando la derivazione il flusso è sale'.  Quindi il problema di riduce al seguente modello differenziale:

sale'(t) = 0.01 − sale(t)/100,   sale(0) = 5.

Nella figura seguente a sinistra è tracciato il campo direzionale di sale'(t) = 0.01 − sale(t)/100 ed è evidenziata la soluzione che corrisponde alla condizione sale(0) = 5.  Il problema richiedeva quanto sale rimane dopo un'ora, ossia quanto vale sale(60).  Dal grafico ricaviamo che  sale(60) ≈ 3.2 (kg).  Sono illustate anche le soluzioni che corrispondono a  sale(0) = 1, in cui la concentrazione iniziale di sali è 1/100 = 0.01, uguale a quella del liquido che viene immesso (la soluzione è quindi la funzione che vale sempre 1), e a  sale(0) = 0.25, in cui la concentrazione iniziale di sali è 0.25/100 = 0.0025, minore di quella del liquido immesso.

(c)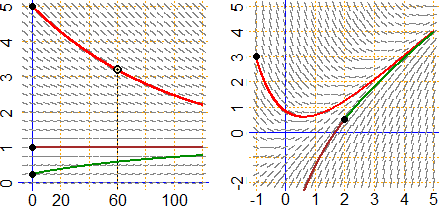

(d)

    La figura a destra rappresenta il campo direzionale di  y'(x) = x − y(x)  e due soluzioni particolari, quella che corrisponde alla condizione  y(−1) = 3  e quella che corrisponde a  y(2) = 0.5.

    Impiegando WolframAlpha:
s'(t) = 0.01 - s(t)/100       s'(t) = 0.01 - s(t)/100, s(0) = 5, what s(60)?
y'(x) = x - y(x)       y'(x) = x-y(x), y(-1) = 3       y'(x) = x-y(x), y(2) = 0.5

I campi direzionali sono ottenibili anche con WolframAlpha: slope field of dy/dx = 0.01-y/100, for 0 <= x <= 100, 0 <= y <= 5 slope field of dy/dx = x-y, for -1 <= x <= 5, -2 <= y <= 5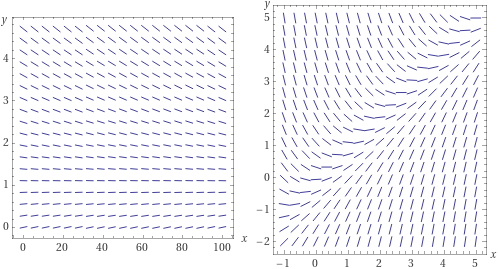

3. Equazioni differenziali del 2º ordine

    Questo argomento, toccato in alcune scuole, è difficile da affrontare nella scuola secondaria superiore. Qui ci limitiamo ad illustrare qualche esempio.

    Il primo esempio rappresenta l'equazione differenziale che esprime la posizione di un oggetto sottoposto ad una forza che sia proporzionale (con un fattore di proporzionalità negativo) alla distanza da una posizione fissata; potrebbe essere un oggetto fissato ad una molla.  Se y è la distanza (in una opportuna unità di misura) e x il tempo (in una opportuna unità di misura), la relazione è del tipo y"(x) = -k·y(x).  Se fisso, in un istante dato, la posizione e la velocità, posso esplicitare y in funzione di x.  Nella figura è rappresentato oltre al grafico della soluzione (in un particolare caso) quello della relazione che lega y e la velocità y'.  Nel caso di questo fenomeno è una curva chiusa in quanto la soluzione è periodica.

Con WolframAlpha: y"(x) = -4*y(x), y(0)=2, y'(0)=0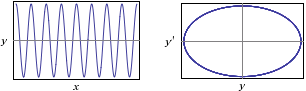

    Gli esempi successivi sono riferiti a situazioni simili alla precedente in cui per , nel primo caso, l'oggetto viene spinto ad ogni passaggio, aumentando l'ampiezza delle oscillazioni, e, nel secondo, si è in presenza di un fluido che smorza le oscillazioni.

Con WolframAlpha: y"(x) = -4*y(x)+cos(2*x), y(0)=2, y'(0)=0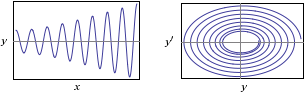
y"(x) = -4*y(x)-y'(x), y(0)=1, y'(0)=3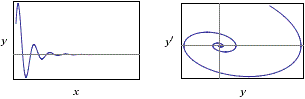

4. Equazioni alle derivate parziali

    Le equazioni differenziali alle derivate parziali (ossia che coinvolgono le derivate parziali della funzione incognita rispetto a più di una variabile), a differenza di quelle ordinarie, hanno soluzioni che non dipendono da costanti arbitrarie ma da funzioni arbitrarie.  Sono usate soprattutto per affrontare alcuni argomenti di fisica.  Ci limitiamo ad alcuni esempi.

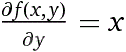
Vediamo un primo esempio di equazione alle derivate parziali (l'incognita è f):     Siamo in grado di risoverla direttamente:  la derivata rispetto a y di f(x,y) è x se f(x,y) è del tipo x·y;  ma possiamo addizionare a x·y un qualunque termine che non contenga y, in quanto la sua derivata rispetto a y è zero.  Quindi le soluzioni sono del tipo:  x·y+g(x)  con g(x) funzione arbitraria.     Verifichiamo la cosa con WolframAlpha (vedi la figura a fianco): introduco  d/dy f(x,y) = x e ottengo f(x,y) = c1(x) + x*y  (qui c1(x) qui indica una generica funzione di x).  OK.     Facciamo due esempi di soluzione, e verifichiamoli: •  f(x,y) = x·y + x³,  ∂f(x,y)/∂y = x+0 = x; •  f(x,y) = x·y + sin(x),  ∂f(x,y)/∂y = x+0 = x.

    Sotto sono illustrati due altri esempi di equazioni alle derivate parziali:

5. Esercizi

e1	So che  g'(x) = 10,  h'(x) = −5,  k'(x) = −x + 0.3.  Che cosa posso dire sul valore di g(x), di h(x) e di k(x)?  E nel caso in cui sappia che i grafici di tutte queste funzioni passano per il punto (7, −2)?

e2	Risolvi con WolframAlpha il problema f'(x) = 4*f(x), f(0) = 1 e, poi, giustifica la risposta ottenuta senza far ricorso al computer.

e3

Un razzo, dopo 60 secondi dal lancio, sta muovendosi verticalmente con l'accelerazione costante di 20 m/s², che, da quell'istante, mantiene per almeno un paio di minuti.  È alla quota di 20 mila metri dal suolo, e, in quell'istante, ha una velocità di salita di 1000 m/s.  Quale quota raggiunge dopo un altro minuto e mezzo?  Che velocità ha in quell'istante? [risolvi il problema con WolframAlpha e indica gli input che hai dato al programma; devi ottenere 116 000 m e 2 800 m/s]

e4	Qual è la funzione y(x) tale che y'(x)=(1+x^2)/x^2, y(-2)=0?  Qual è l'intervallo di massima ampiezza in cui essa è definita?

e5	Risolvi con WolframAlpha il problema  y"(x)=sin(x), y(π)=2, y'(π)=−1  e verifica, a mano, la soluzione trovata.  Saresti stato in grado di risolvere il problema senza usare WolframAlpha?  Come?

e6	Risolvi con WolframAlpha il problema  y"(x)=cos(x), y(0)=0, y'(0)=1  e verifica, a mano, la soluzione trovata.  Saresti stato in grado di risolvere il problema senza usare WolframAlpha?  Come?

e7	Data l'equazione differenziale y'(x) = 1+x/(y(x)^2+1) tracciane il campo direzionale in [−8,4]×[−4,4].  Traccia, poi, i grafici delle due soluzioni tali che y(−6)=1 e che y(2)=0. Trovane i valori che esse hanno in, rispettivamente, 2 e −2, e confrontali con quelli ottenibili con WolframAlpha.

e8

Data l'equazione differenziale y'(x) = (y-x)/(x-4*y) tracciane il campo direzionale in [−2,2]×[−2,2].  Trova quanto vale in 2 la soluzione che passa per (−2,1.5) e confronta il valore con quello che ottieni con WolframAlpha.  Rivedi, poi, l'ultimo esempio discusso nel paragrafo 3; quindi cerca quali sono le soluzioni passanti per (−2,1) e per (−2,1/2); confronta poi i valori trovati con quello che ottieni con WolframAlpha e spiega perché questi sono sbagliati.

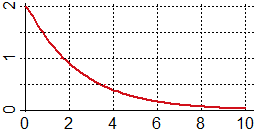
e9      In modo simile a quello con cui sono studiate le equazioni differenziali del 2º ordine presentate nel 4º paragrafo, studia l'equazione differenziale che corrisponde al fenomeno in cui l'oggetto è immerso in un fluido che smorza le oscillazioni secondo un fattore che è 10 volte quello dell'ultimo esempio [-10·y'(x) invece di -y'(x)], la "distanza" inziale dell'oggetto dalla posizione di riferimento è 1, la "velocità" iniziale è 0.  Dovresti ottenere che y in funzione di x ha un grafico simile a quello a lato.

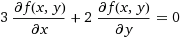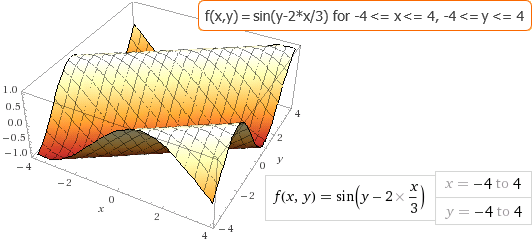
	e10      Introducendo  3*(d/dx f(x,y)) + 2*(d/dy f(x,y)) = 0,  trova con WolframAlpha le soluzioni dell'equazione alle derivate parziali considerata a lato.  Sotto è tracciato il grafico di una soluzione.  Individuane altre e scrivi le istruzioni per rappresentarne il grafico con WolframAlpha.