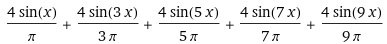Analisi+

Approfondimenti di Analisi Matematica

1. Richiami
2. I polinomi (e le serie) di Taylor
3. Le serie di Fourier
4. Il gradiente
5. Esercizi

1. Richiami

Sappiamo che una funzione può essere approssimata in un punto dato, in cui sia derivabile, dalla funzione che ha per grafico la sua tangente, che è una funzione polinomiale di 1° grado, o una funzione costante. Più in generale una funzione pu` essere approssimata con una funzione polinomiale anche di grado maggiore. Nel primo paragrafo di questa scheda approfondiremo questo aspetto. Nei successivi, che sono da intendere come approfondimenti per alcuni tipi di scuole, saranno approfonditi alcuni argomenti più o meno collegati al precedente: metodi per approssimare funzioni con somme di seni e coseni, la derivazione di una funzione di più variabili, …

2. I polinomi (e le serie) di Taylor

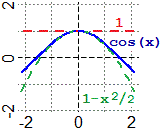
La figura a lato ricorda che, per x → 0, cos(x)−1 ≈ −x²/2, ovvero cos(x) ≈ 1−x²/2: posso approssimare il grafico di cos attorno a 0 con una parabola. Vediamo perché.
In 0 cos ha come tangente la retta y=1. Quindi, attorno a 0, è approssimabile con la funzione che vale costantemente 1. La pendenza di questa retta l'ho trovata calcolando la derivata di cos in 0: D(cos) = −sin e −sin(0) = 0.
Cerco ora la funzione polinomiale P di 2º grado x → a₀ + a₁x + a₂x² col grafico che meglio approssimi la curva attorno all'ascissa 0. Impongo che P abbia una pendenza che vari attorno a 0 con la stessa velocità con cui varia quella di cos. Posso esprimere ciò imponendo che la derivata della sua derivata in 0 coincida con quella di cos.

In breve occorre che P(0) = cos(0) (il polinomio P in 0 valga quanto la funzione cos), P'(0) = cos'(0) (P in 0 abbia la stessa pendenza di cos), P''(0) = cos''(0) (P in 0 abbia grafico incurvato come quello di cos):
P(0) = cos(0) = 1, P'(0) = cos'(0) = −sin(0) = 0, P''(0) = −sin'(0) = −cos(0) = −1.
P(0) = [a₀ + a₁x + a₂x²]_x=0 = a₀, P'(0) = [a₁ + 2·a₂·x]_x=0 = a₁, P"(0) = [2·a₂]_x=0 = 2a₂.
Quindi: a₀ = 1, a₁ = 0, a₂ = −1/2. Ossia: P(x) = 1 − x²/2

Data una funzione F che sia più volte derivabile nel punto Q, posso trovare un polinomio che ne approssimi l'andamento nei pressi di Q anche di grado maggiore al secondo. Basta che imponga che siano uguali a quelle di F anche le sue derivate in Q di ordine maggiore al secondo (F''' è la derivata di F'', F'''' è la derivata di F''', …). Polinomi di tal genere sono chiamati polinomi di Taylor (dal nome dello studioso inglese che, intorno al 1715, ne ha approfondito lo studio, pochi anni dopo che erano stati "inventati").

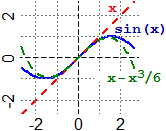
Vediamo qual è il polinomio P(x) di 3º grado a₀ + a₁x + a₂x² + a₃x³ che approssima sin(x) nei pressi di 0. Occorre che:
P(0) = [a₀ + a₁x + a₂x² + a₃x³]_x=0 = a₀, P'(0) = [a₁ + 2·a₂·x + 3·a₃·x²]_x=0 = a₁, P"(0) = [2·a₂ + 3·2·a₃·x]_x=0 = 2a₂, P'''(0) = [3·2·a₃]_x=0 = 6a₃,
e che tali valori siano eguali a:
F(0) = sin(0) = 0, F'(0) = sin'(0) = cos(0) = 1, F"(0) = cos'(0) = −sin(0) = 0, F'''(0) = −sin'(0) = −cos(0) = −1.
Quindi: a₀ = 0, a₁ = 1, a₂ = 0, a₃ = −1/6. Ossia: P(x) = x − x³/6.

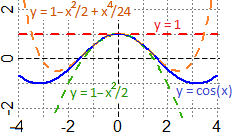Qual è il polinomio P(x) di 4º grado a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ che approssima cos(x) nei pressi di 0? Occorre che:
P(0) = [a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴]_x=0 = a₀, …, P⁽⁴⁾(0) = [4·3·2·a₄]_x=0 = 24a₄ (P⁽⁴⁾ sta per P''''),
e che questi valori siano eguali a:
F(0) = cos(0) = 1, F'(0) = cos'(0) = −sin(0) = 0, F"(0) = −sin'(0) = −cos(0) = −1, F⁽³⁾(0) = −cos'(0) = sin(0) = 0, F⁽⁴⁾(0) = sin'(0) = cos(0) = 1.
Quindi: a₀ = 1, a₁ = 0, a₂ = −1/2, a₃ = 0, a₄ = 1/24. Ossia: P(x) = 1 − x²/2 + x⁴/24.

Generalizzando si può dimostrare che se F è una funzione ad 1 input ed 1 output derivabile nel punto a fino all'ordine N, allora per x → a F(x) è eguale a P(x) a meno di un infinitesimo di ordine superiore a (x−a)^N, dove P(x) è il polinomio di Taylor così definito:

F(a) + Σ_{k = 1..N} F^(k)(a)·(x-a)^k / k!

Questo termine viene chiamato polinomio di Taylor di ordine N ma non è detto che sia un polinomio di grado N. Potrebbe infatti essere di grado minore: basta che F^(N)(a) sia nullo. Ad esempio 1−x²/2 è il polinomio di Taylor di sin sia di ordine 2 che di ordine 3, in quanto se sviluppo la formula precedente fino ad N = 3 ottengo lo stesso valore ottenuto per N = 2 in quanto la derivata 3ª in 0 è −sin(0) che vale 0.

Volendo, si può dimostrare che se esiste in a anche la derivata N+1-esima, allora il resto, ossia la differenza tra F(x) e P(x), è infinitesimo non solo di ordine superiore a (x−a)^N, ma di ordine eguale o superiore a (x−a)^N+1. Per indicare questi due concetti si usano notazioni differenti: ad es: F(x) = P(x) + o((x−a)²) ("o piccola") indica la presenza di un termine che per x → a è trascurabile rispetto a G(x); invece F(x) = P(x) + O((x−a)³) ("o grande") indica la presenza di un termine che per x → a è dello stesso ordine o è trascurabile rispetto a G(x).

1
Verifica che il polinomio che approssima sin(x) attorno a 0 a meno di un infinitesimo di ordine superiore a 6 è:
P(x) = 0 + 1·x + 0/2·x² - 1/6·x³ + 0/24·x⁴ + 1/120·x⁵ + 0/720·x⁶ = x − x³/6 + x⁵/120

Sotto sono rappresentate le funzioni seno e coseno e alcuni dei relativi polinomi di Taylor attorno a 0.

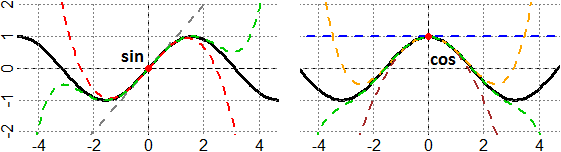
I polinomi di Taylor sono facilemente determinabili con WolframAlpha:

taylor polynomial of sin(x) at x=0

x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880 - x^11/39916800 + O(x^13)

2
Utilizza WolframAlpha per trovare i polinomi di Taylor della funzione coseno rappresentati nella figura precedente.

3
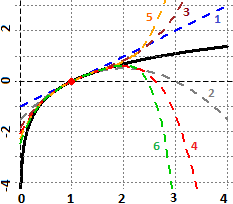
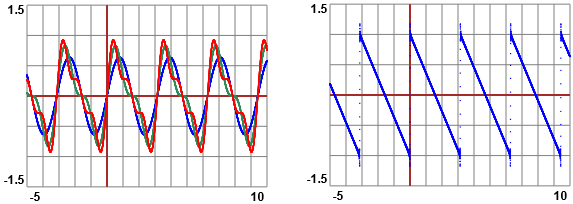
So che la funzione log è definita per input positivi, che per x → 0+ log(x) → −∞ e che per x → ∞ log(x) → ∞, come si è ricordato anche nel riassunto di matematica richiamato all'inizio della scheda. So che log(1)=0. Posso approssimare con un polinomio log attorno ad 1. Se uso WolframAlpha e batto taylor polynomial of log(x) at x=1 ottengo:
x−1 − (x−1)²/2 + (x−1)³/3 − (x−1)⁴/4 + (x−1)⁵/5 − (x−1)⁶/6 + O((x−1)⁷)
A lato sono rappresentati graficamente i polinomi di Taylor fino a quello di ordine 6.
Prova a determinarli anche "a mano", fino a quello di ordine 3.

4
Prova ad ottenere, da quanto visto nell'esercizio precedente, l'approssimazione polinomiale di log(1+x) attorno a 0.
Poi verifica la risposta con WolframAlpha battendo taylor polynomial of log(1+x) at x=0.

5
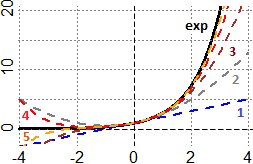
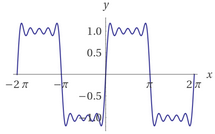
A sinistra è rappresentata graficamente la funzione exp e alcuni suoi polinomi di Taylor attorno a 0. Verifica con WolframAlpha che: exp(x) = 1 + x + x²/2 + x³/3! + … + x⁶/6! + O((x−1)⁷)

Posso anche stimare l'errore:

F(x) = F(a) + Σ_{k = 1..N} F^(k)(a)·(x−a)^k / k! + R(x)

dove R(x) = F^(N+1)(c)·(x−a)^N+1/ (N+1)!

• Ecco per esempio come valutare la precisione con cui x−x³/6 approssima sin(x) nell'intervallo [−0.1, 0.1].

Per x = 0 x−x³/6 = 0. R(x) = D⁽⁵⁾(sin)(c) / 5! · x⁵ = cos(c) · x⁵ / 5!

|cos(x)| ≤ 1; quindi |R(x)| ≤ 1·0.1⁵/5! = 1/12·10⁻⁶ < 10^-7. Stimo ad es. sin(0.1): 0.1−0.1³/6 = 0.09983333. L'errore è minore di 10^-7. Quindi assumo sin(0.1) = 0.09983333±10^-7. 0.09983323 = 0.09983333-10^-7 < sin(0.1) < 0.09983333+10^-7 = 0.09983343; posso assumere con sicurezza l'arrotondamento sin(0.1) = 0.099833. Se potessi disporre di una calcolatrice otterrei sin(0.1) = 0.09983342.

Calcoliamo, usando il polinomio di Taylor, il limite di una funzione, ad es. (sin(x)³−x·log(1+x²)) / (x⁵(1−cos(x))) per x → 0. È un calcolo concettualmente semplice ma un po' complicato calcolisticamente.
• Numeratore e denominatore tendono a 0. Approssimo il denominatore.
x⁵(1−cos(x)) = x⁵·(x²/2 + O(x⁴)) = x⁷/2 + O(x⁹)
• Approssimo il numeratore. Uso il fatto che attorno a 0 (vedi es. 4) log(1+x) = x − x²/2 + x³/3 + …
log(1+x²) = x² − x⁴/2 + x⁶/3 + O(x⁸)
x·log(1+x²) = x³ − x⁵/2 + x⁷/3 + O(x⁹)
sin(x) = x − x³/3! + O(x⁵)
sin(x)³ = (x−x³/3!+O(x⁵))·(x−x³/3!+O(x⁵))·(x−x³/3!+O(x⁵)) = x³ − x⁵/2 + 13·x⁷/120 + O(x⁹)
sin(x)³−x·log(1+x²) = (13/120−1/3)·x⁷ + O(x⁹) = −9/40·x⁷ + O(x⁹)
• A questo punto posso concludere che per x → 0:
(sin(x)³−x·log(1+x²)) / (x⁵(1−cos(x))) = ( x⁷/2 + O(x⁹) ) / ( −9/40·x⁷ + O(x⁹) ) → −9/20 = −0.45.
È stato un po' faticoso, ma ci siamo arrivati. Ovviamente si poteva fare tutto facilmente con WolframAlpha introducendo:
limit(sin(x)^3-x*log(1+x^2)) / (x^5*(1-cos(x))) as x -> 0

Chiudiamo questo paragrafo con una osservazione. Prima ricordiamo che, come abbiamo visto pi volte, si possono considerare somme infinite di numeri. Ad esempio, dalla scuola elementare, so che la somma di 0.3, 0.03, 0.003, 0.0003, … è 0.3333… = 1/3. In breve: 0.3 + 0.03 + 0.003 + 0.0003 +… = 1/3. Nella scuola superiore ho visto che, volendo, posso esprimere ciò considerando la successione s₁, s₂, s₃, … dove s_n = 3 + 3/10¹ +…+ 3/10ⁿ e dire che il limite di s_n per n → ∞ è 1/3. Successioni come s_n che esprimono una somma di numeri a₁ + a₂ +…+ a_n vengono chiamate serie..
Non tutte le serie convergono. Ad esempio 1+2+3+… non converge in quanto le somme 1, 1+2, 1+2+3, … non hanno risultati che si stabilizzano. Neanche 1 + 1/2 + 1/3 +… converge, come posso verificare con WolframAlpha battendo 1+1/2+1/3+1/4+... (prova anche a cercare, su WolframAlpha, harmonic series).

La cosa può essere dimostrata:
1 + 1/2 + 1/3 + … = 1 + (1/2 + 1/3 + ... + 1/10) + (1/11 + ... + 1/100) + (1/101 + ... + 1/1000) + ... >
1 + (1/10 + 1/10 + ... + 1/10) + (1/100 + ... + 1/100) + (1/1000 + ... + 1/1000) + ... =
1 + 9·1/10 + 90·1/100 + 900·1/1000 + ... = 1 + 0.9 + 0.9 + 0.9 + ...

Se come addendi invece di numeri considero delle funzioni f₁(x), f₂(x), f₃(x), … parlo di serie di funzioni. Per quanto ricordato sopra, è ovvio che per alcuni valori di x una serie f₁(x) + f₂(x) + f₃(x) + … possa convergere e per altri possa non convergere (o, come si usa dire, possa divergere).
Se una funzione F ammette derivate di ogni ordine in un intervallo I contenente a posso considerare i polinomi di Taylor attorno ad a di ogni grado, ovvero considerare la serie di Taylor di punto iniziale a:

F(x) = F(a) + F'(a)·(x−a) + F"(a)·(x−a)²/2 + F⁽³⁾(a)·(x−a)³/6 + ...
= F(a) + Σ_{k = 1..∞} F^(k)(a)·(x−a)^k / k!

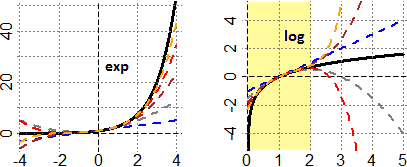
Senza approfondire ulteriormente l'argomento, osserviamo che gli sviluppi in serie di Taylor di exp, sin e cos attorno a 0 convergono su tutto R, mentre quello di log attorno ad 1 converge solo nell'intervallo (0, 2]. Vedi, qui sotto, i grafici di exp e log e quelli di alcuni loro polinomi di Taylor. Lasciamo ad un esercizio indicazioni per eventuali approfondimenti.

3. Le serie di Fourier

Si può dimostrare che ogni funzione F continua in un intervallo [−h, h] può essere espressa come una serie di Fourier, ossia come una serie infinita di seni e di coseni:

F(x) = A₀ + Σ_{k = 1..∞} (A_k·cos(k·x) + B_k·sin(k·x))

I termini A_k·cos(k·x) + B_k·sin(k·x) sono funzioni periodiche di frequenza crescente, e sono chiamati, in ordine, prima, seconda, terza, ... armonica.
Ogni funzione periodica (anche non continua) può essere approssimata con un polinomio di Fourier. Ci limitiamo a vedere alcuni esempi. Se proseguirai negli studi potrai sviluppare il tema (in un esercizio sono comunque presenti indicazioni per eventuali approfondimenti).

Jean-Baptiste-Joseph Fourier (1768-1830) fu un matematico e fisico francese. Tra l'altro, studiando la propagazione del calore, introdusse gli sviluppi in serie che portano il suo nome.

1, 2 e 3 addendi 100 addendi

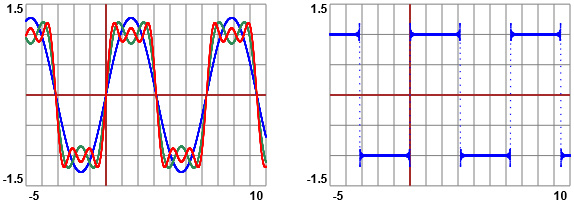
f(x) = 4/π·sin(x) + 4/π·sin(3x)/3 + 4/π·sin(5x)/5 + 4/π·sin(7x)/7 + ...

La "somma" è la funzione che associa -1 agli input tra -π e 0, 1 a quelli tra 0 e π. Possiamo verificare la cosa con WolframAlpha digitando "fourier series expand" e introducendo gli input scritti qui sotto (in blu):

fourier series expand
  function to expand  Piecewise[ { {-1, -pi < x < 0}, {1, 0 < x < pi} } ]
            variable  x
               order  10

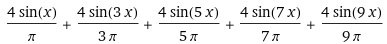Altri esempi:

1, 2 e 3 200 addendi

f(x) = 4/π·sin(2x)/2 + 4/π·sin(4x)/4 + 4/π·sin(6x)/6 + 4/π·sin(8x)/8 + ...
1, 2 e 3 addendi 100 addendi

f(x) = π²/3 + 4·(-1)¹/1²·cos(1·x) + 4·(-1)²/2²·cos(2·x) + 4·(-1)³/3²·cos(3·x) + ...

Questo argomento ha molte applicazioni in fisica, per studiare i fenomeni ondulatori, ad esempio di natura ottica e sonora, ed anche in molti ambiti tecnologici (per realizzare apparecchi fotografici digitali, per restaurare film e registrazioni, per memorizzare le impronte digitali, …).

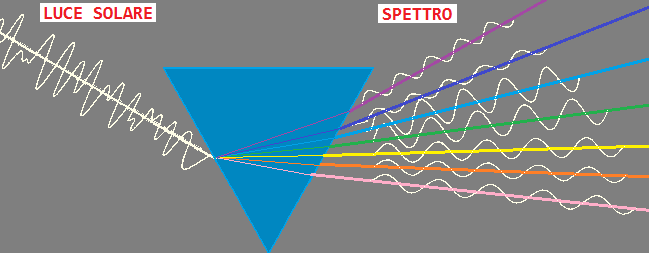
Per dare un'idea delle applicazioni ci limitiamo a riportare la seguente immagine, in cui si vede un raggio solare che entra in un prisma a sezione triangolare e ne esce separato spazialmente in colori "puri", i colori dell'arcobaleno (essa mostra come un'onda possa essere espressa come sovrapposizione di onde sinusoidali).

4. Il gradiente

Abbiamo introdotto il concetto di derivata parziale. Ora accenniamo al concetto di gradiente per venire incontro alle esigenze di chi lo trova nei programmi scolastici. Si tratta, comunque, di un tema che può essere approfondito solo negli studi universitari.

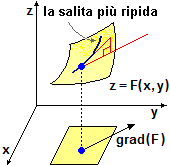
Data una funzione F di due variabili, il suo gradiente, indicato con grad(F) o con ∇F, è la funzione vettoriale che ha come componenti le due derivate parziali di F: ∇F(x,y) = (∂F(x,y)/∂x, ∂F(x,y)/∂y).

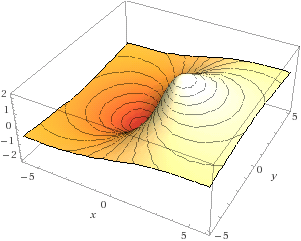
Calcolo ad esempio il gradiente di F: (x,y) → 6 x / (2+x²+y²). È facile calcolare le due derivate parziali, ma lo faccio con WolframAlpha. Ottengo:

grad ( 6*x/(2+x^2+y^2) )
( (6*(-x^2+y^2+2))/(x^2+y^2+2)^2, -(12*x*y)/(x^2+y^2+2)^2 )

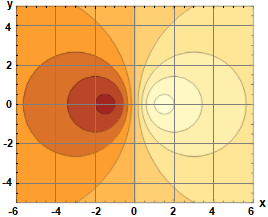
Vediamone il significato geometrico. Traccio prima il grafico della funzione, e le sue curve di livello.

I grafici sono stati realizzati con WolframAlpha mediante il comando plot z = 6*x/(2+x^2+y^2), -6 <= x <= 6, -5 <= y <= 5

Vedo che ci sono un punto di massimo ed uno di minimo. So che questo accade dove le derivate prime si annullano. Ciò equivale al fatto che il gradiente sia (0, 0). Vediamo dove accade: -x^2+y^2+2 = 0 & 12*x*y = 0; ovvero: y = 0 & x = ±√2. Si vede dalla figura soprastante che i punti (√2, 0) e (−√2, 0) sono proprio i punti di massimo e di minimo della funzione.

WolframAlpha automatizza questi procedimenti:

min z = 6*x/(2+x^2+y^2), -6 <= x <= 6, -5 <= y <= 5 ottengo:
min{6*x/(2+x^2+y^2) | -6<=x<=6 & -5<=y<=5} = -3/sqrt(2) at (x,y) = (-sqrt(2),0)

max z = 6*x/(2+x^2+y^2), -6 <= x <= 6, -5 <= y <= 5 ottengo:
max{6*x/(2+x^2+y^2) | -6<=x<=6 & -5<=y<=5} = 3/sqrt(2) at (x,y) = (sqrt(2),0)

Vediamo che cosa rappresenta il gradiente nei punti dove non si annulla.
Nel caso delle funzioni di una variabile il valore assoluto della derivata in un punto è la pendenza del grafico in quel punto, mentre il segno della derivata rappresenta se la funzione cresce o decresce.
Nel caso di una funzione F di due variabili ci interessa la direzione in cui avviene il cambiamento con massima pendenza, e il valore di questa pendenza. Il gradiente di F rappresenta il vettore (orizzontale) che indica la direzione in cui F varia più rapidamente. Il modulo del gradiente rappresenta la velocità di questa variazione, ovvero la pendenza (positiva) della superficie lungo tale direzione. Le componenti del gradiente indicano la rapidità della variazione nelle direzioni degli assi x e y.
È intuitivo capire che il gradiente in P, se diverso da 0, è perpendicolare alla curva di livello passante per P. La direzione di una curva di livello passante per un punto P indica la direzione lungo cui il gradiente si annulla.

Le componenti del gradiente (ossia le due derivate parziali) indicano l'intensità della velocità della variazione nelle direzioni degli assi. In generale, fissata una qualunque direzione, la proiezione lungo di essa del gradiente di F indica l'intensità della velocità con cui varia F in tale direzione. Se u è il versore unitario che rappresenta la direzione, questa proiezione non è altro che il prodotto scalare (dot product) ∇(F)·u.

Come nel caso di una funzione in una variabile il fatto che la sua derivata in x sia nulla non è sufficiente per dedurre che in x vi sia un max o un min relativo (può esservi un flesso), così in quello di una funzione di due variabili non basta che il gradiente in P sia nullo, ossia che P sia un punto stazionario, affinché in P vi sia un estremo relativo. Nel caso precedente per (√2,0) e (−√2,0) la cosa ci era assicurata dall'andamento del grafico. Eccone uno in cui ciò non accade.

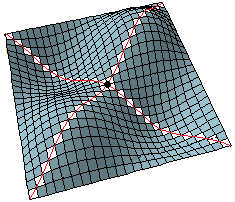
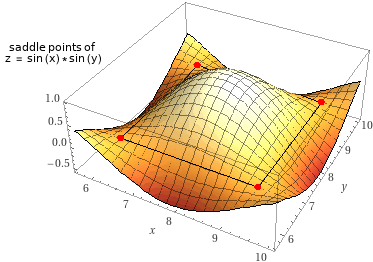
Consideriamo la funzione F: (x,y) → sin(x)·sin(y). Ecco i grafici con WolframAlpha mediante il comando plot z = sin(x)*sin(y), -PI*3/2 <= x <= PI*3/2, -PI*3/2 <= y <= PI*3/2

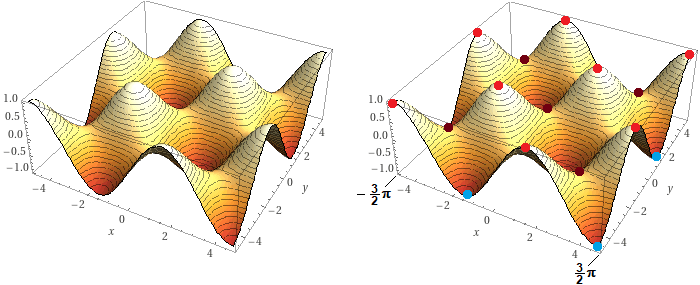
I punti segnati con dei pallini sono quelli in cui si azzera il gradiente, che è (cos(x)·sin(y), sin(x)·cos(y)), ossia (0, 0), (± π/2, ± π/2), e tutti gli altri punti che si ottengono da questi aggiungendo "periodi". Abbiamo segnato con dei pallini rossi i punti di massimo e con dei pallini celesti i punti di minimo, le cui coordinate potremmo trovare con gli stessi comandi max e min usati sopra.

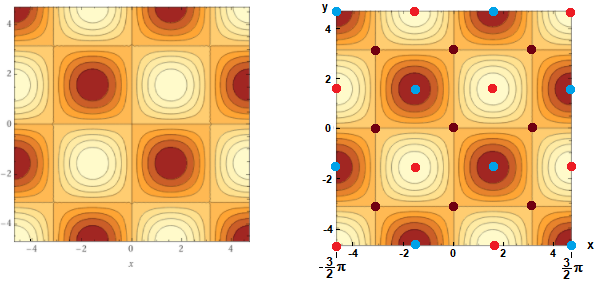
Nei punti segnati in nero, (0, 0) e gli altri punti dove i riquadri si incrociano - ossia (π.0), (0,π), (π,π), … - non si hanno minimi o massimi. Sono punti, come si vede nella figura sotto a sinistra, di minimo lungo la "cresta dei monti" e di massimo lungo la "strada del valico". Per la loro forma vengono chiamati punti di sella. Possiamo individuarne la presenza con WolframAlpha mediante il comando saddle points of z = sin(x)*sin(y); vedi la figura sotto a destra.

Nei punti di sella le curve di livello si intersecano. Avvicinandosi a quelli di minimo e di massimo le curve di livello tendono a ridursi ad un punto.

Avremmo potuto visualizzare i punti stazionari anche con stationary points sin(x)*sin(y)

5. Esercizi

e1
Trova il polinomio di Taylor di e^−2x attorno a 0 usando il comando taylor polynomial of exp(-2*x) at x=0 in WolframAlpha. Spiega come puoi ottenere lo stesso polinomio utilizzando lo sviluppo di e^x visto nella scheda.

e2
Determina i polinomi di Taylor di cos attorno a 0 di ordine 2, 4 e 6. Calcolane il valore in π/6. Stabilisci quale approssimazione di cos(π/6) puoi dedurre da tali valori. Confronta quanto hai ottenuto col valore effettivo di cos(π/6).

e3
Occorre stare attenti usando WolframAlpha per studiare la convergenza di una serie quando il risultato è un intervallo finito. Può essere che dia la convergenza solo per la parte interna dell'intervallo mentre la serie potrebbe convergere anche in uno degli estremi. Conviene allora fare la verifica, sempre con WolframAlpha, come spiega il seguente esempio. Svolgi i calcoli descritti. Che cosa ottieni?
taylor polynomial of log(1+x^2) at x=0 1-1/2+1/3-1/4+...

e4
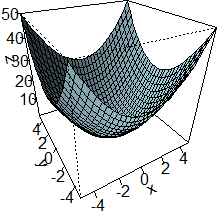
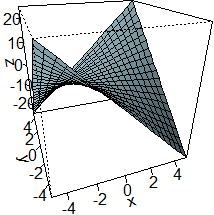
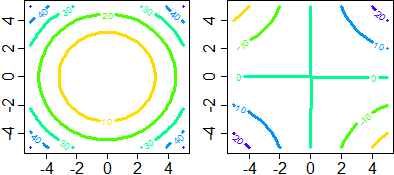
Considera le funzioni (x,y) → x²+y² e (x,y) → x·y. Sotto sono tracciati i grafici di esse e quelli di alcune loro curve di livello. Associa ad ogni funzione il grafico di essa e delle sue curve di livello. Verifica la risposta con WolframAlpha.

e5
Abbiamo visto che 1+1/10+1/10²+1/10³+… converge a 1.111… = 1+1/9. Abbiamo pure visto che 1+1/2+1/2²+1/2³+… converge a 2. In modo simile si dimostra che, se |x| < 1 1+x+x^2+x^3+... converge. Verifica la cosa con WolframAlpha e trova, in funzione di x, il valore a cui converge; controlla che il risultato trovato sia in accordo con i due esempi precedenti. Analogamente si dimostra che converge ogni serie x₁+x₂+x₃+… tale che esista un K positivo e minore di 1 per cui da un certo posto in poi |x_n+1| sia minore di K·|x_n|. Verifica, usando questo criterio, che la serie 1+1/2+1/3!+1/4!+... converge; prova a trovare quanto vale la somma. Dimostra che la serie 1+1/2+1/3+1/4+... non verifica questo criterio.