Funzioni di più variabili

  1. Richiami
  2. Grafici di funzioni di due variabili e superfici
  3. Derivazione delle funzioni di due variabili. Primo esempio
  4. Altri esempi. La continuità.
  5. L'hessiano
  6. Esercizi
Sintesi

1. Richiami

    Abbiamo considerato in molte occasioni funzioni a più input:  la funzione "somma" che ai numeri x ed y associa x+y;  la funzione "media" che ad un insieme di numeri associa il loro valor medio;  la funzione "simmetria rispetto (0,0)" che al punto (x,y) associa il punto (−x,−y); …. In questa scheda ci occuperemo delle funzioni che hanno come input coppie di numeri reali e come output numeri reali.  Queste funzioni vengono chiamate anche funzioni reali di due variabili reali.  Il paragrafo seguente è per tutti, i successivi sono da intendere come approfondimenti per alcuni tipi di scuole.

2. Grafici di funzioni di due variabili e superfici

    Sotto a sinistra è rappresentata la retta x+y = 3, ovvero il grafico della funzione x → 3 − x. Esso passa per i punti (3, 0) e (0, 3).
    A destra è rappresentato il piano x+y+z = 3, che è grafico della funzione (x, y) → 3 − (x + y); passa per i punti (3, 0, 0), (0, 3, 0) e (0, 0, 3).  In realtà ne è raffigurata solo la parte che sta in una delle 8 zone in cui lo spazio è suddiviso dai piani che passano per le varie coppie di assi:  quella corrispondente a  x ≥ 0, y ≥ 0 e z ≥ 0.

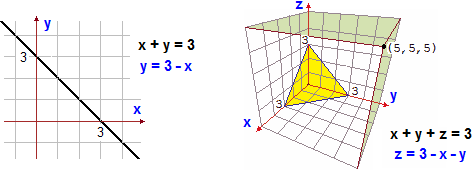
    Così come le rette non perpendicolari all'asse x sono interpretabili come grafici di funzioni a 1 input e 1 output reali, così i piani non perpendicolari al piano di input sono interpretabili come grafici di funzioni a 2 input e 1 output reali.
    Abbiamo visto che un cerchio non può essere pensato come il grafico di una funzione di una variabile:  ad ogni ascissa a di un punto interno al diametro corrispondono due punti del cerchio, uno che sta sopra e l'altro che sta sotto al diametro. Possiamo rappresentare come grafico di una funzione il semicerchio superiore o quello inferiore. Nel caso del cerchio di raggio 1 centrato in (0, 0), il semicerchio superiore è descrivibile come il grafico della funzione F: x → √(1 − x²). Vedi la figura sotto a sinistra.

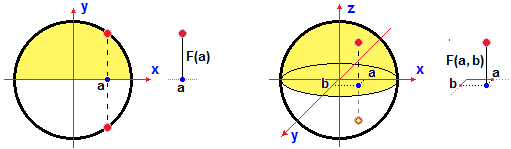
    Analogamente una sfera non può essere pensata come il grafico di una funzione di due variabili, mentre possono esserlo o la semisfera che sta al di sopra del piano orizzontale che la taglia in due parti uguali o quella che sta al di sotto di essa.  Cerchiamo di descrivere analiticamente la funzione F che ha come grafico la metà superiore della sfera di raggio 1 centrata in (0, 0, 0). Vedi la figura sopra a destra.

    Un punto P = (x,y,z) della sfera (vedi la figura sotto a sinistra, che riprende la figura precedente) dista 1 da O, quindi abbiamo, per il teorema di Pitagora:

    z = √(1 − (x² + y² ))  è l'equazione della semisfera rappresentata sopra al centro,  z = −√(1 − (x² + y² ))  è l'equazione dell'altra semisfera (a destra), simmetrica alla precedente rispetto al piano z = 0.  Le due figure sono state tracciate con WolframAlpha mediante il comando

    La funzione F considerata sopra è dunque  (x, y) → √(1 − (x² + y² )).

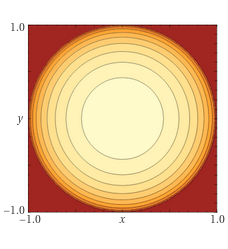
    Tracciata la superficie con  3d plot z=sqrt(1-x^2-y^2), x=-1..1, y=-1..1  posso anche visualizzarla evidenziando le curve di livello (figura sotto a sinistra), che posso tracciare meglio (figura a destra) col seguente comando:

    Posso anche cambiare punto di vista:  3d plot z=sqrt(1-x^2-y^2), x=-1..1, y=-1..1 from (10,1,1.5)  (figura sotto a sinistra).  Una diversa rappresentazione si piò ottenere tracciando la superficie impiegando una descrizione parametrica (figura sotto a destra), in modo simile a quanto visto in rette tangenti e curve per descrivere le curve in forma parametrica, usando ad esempio u e v come parametri:

Posso, poi, considerare la semisfera come frutto della rotazione attorno all'asse verticale z del semicerchio  z = √(1-x²).  Posso far eseguire la rotazione a WolframAlpha mediante il comando: rotate z=sqrt(1-x^2), x=0..1, about the z-axis     A destra, infine, la sfera tracciata col comando: 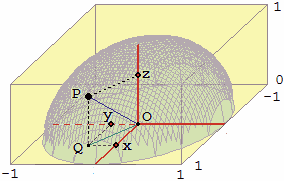plot x^2 + y^2 + z^2 = 1

    Si possono ottenere, ruotando, anche superfici che non sono grafici di funzione:

Come grafici di funzioni di 2 variabili posso descrivere, oltre alle semisfere, altre superfici :  coni, figure ottenute dalla rotazione di una parabola (come quella qui a sinistra) o una iperbole, e, ad es., figure come la seguente, sotto a sinistra, di equazione  z = sin(x) + cos(2 y), della quale, sotto a destra, sono tracciate anche alcune curve di livello.     La figura ottenuta dalla rotazione di una parabola rientra nelle superfici chiamate quadriche, di cui, qui, puoi trovare una descrizione.

    Si può generalizzare il concetto di integrazione dal caso di 1 variabile a quello di 2, in modo da calcolare il volume che sta tra la superficie grafico di una funzione di due variabili e il piano z = 0. Nel caso precedente troverei, in modo diverso da quello considerato qui il volume, che il volume della semisfera di raggio unitario è 2/3·π.
    Potrei anche, analogamente, valutare la probabilità che una coppia di variabili casuali cada in certo insieme calcolando l'integrale su di esso della funzione di due variabili che ne rappresenta la distribuzione ( sistemi di variabili casuali).

3. Derivazione delle funzioni di due variabili. Primo esempio.

    Parto da un esempio: la funzione F: (x,y) → x·y². La rappresento graficamente con del software. Continuo ad usare il gratuito WolframAlpha. Poi cercherò di capire come potrei studiarne le caratteristiche senza ricorrere ai grafici.

    Ho usato vari strumenti:
plot z = x*y^2, x from -3 to 3, y from -3 to 3    mi ha fornito il primo grafico (ho scelto il tracciamento delle "contour lines");
plot z = x*y^2, x from -2 to 2, y from -2 to 2, z from -8 to 8 view from(2,5,1)    mi ha dato il secondo (ho scelto l'intervallo per z e il punto di vista);
x*y^2=0, x*y^2=3, x*y^2=3, x*y^2=9, x*y^2=-3, x*y^2=-6, x*y^2=-9, x from -3 to 3, y from -3 to 3    ha tracciato curve di livello a varie quote.

    Ho capito che la funzione ha andamento orizzontale solo lungo una retta alla quota 0.  Non ha punti di massimo relativo o di minimo relativo, ossia non presenta cupolette all'insù o all'ingiù.  Confrontando il grafico con l'espressione della funzione, F(x,y) = x·y², capisco anche che sezionando la superficie con piani verticali del tipo x = h ottengo delle parabole:  sono le curve z = h·y².

    Vediamo come arrivare alle stesse conclusioni con dei "calcoli". Si usano le derivate parziali, ossia le derivate di F(x,y)  (= x·y²)  pensando x o y come costante. La derivata parziale rispetto ad x vale y² in quanto penso ad x come l'unica variabile  (y² deve essere intesa come una costante, per cui "porto fuori" y² e derivo x, che fa 1).  Essa si indica in vari modi. Ad esempio:

D(x·y², x)      ∂ x·y² / ∂x      ∂ F(x,y) / ∂x      F_x(x,y)

    Analogamente la derivata parziale rispetto ad y vale x·2·y, ossia 2 x y. Posso indicarla così:

D(x·y², y)      ∂ x·y² / ∂y      ∂ F(x,y) / ∂y      F_y(x,y)

    Per il calcolo con WolframAlpha mi conviene battere d(x*k^2)/dx mettendo k invece di y.

    Per esprimere il valore della derivata parziale in un punto, ad esempio la derivata parziale rispetto ad y in (3,0), posso scrivere  D(x·y²,y) _x=3,y=0  o, ad esempio, se indico con x e y le due variabili,  ∂ F(3,0) / ∂y.

1

Calcola le derivate rispetto ad x e rispetto ad y di sin(x) + cos(2 y) e valuta quanto valgono in (0,0).

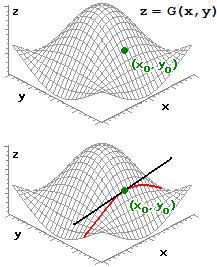
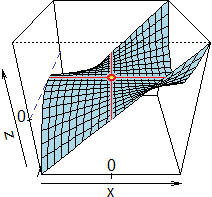
Suppongo che il grafico di  z = G(x,y)  sia la superficie rappresentata a lato.  Considero la derivata parziale di G rispetto a x nel punto (x0,y0).     Mantenendo y costante e facendo variare x, traccio una curva (in rosso) che rappresenta l intersezione della superficie con il piano verticale di equazione y = y0.  La derivata parziale  Gx(x0, y0)  rappresenta la pendenza della retta tangente a questa curva nel piano verticale di equazione y = y0.     Considero, ora, la figura seguente:

Nel punto (a,b) entrambe le derivate parziali di G sono nulle.  In questo caso in (a,b) G ha un punto di massimo.  In altre situazioni in un punto in cui entrambe le derivate parziali siano nulle potrebbe esservi un minimo.  Ma non è detto che ciò accada.  Così come una funzione in una variabile derivabile che in un punto abbia derivata nulla potrebbe avere ivi un flesso (vedi), qualcosa di analogo potrebbe accadere per le funzioni in due variabili.  Ritorniamo alla funzione F considerata all'inizio del paragrafo, rappresentata qui a sinistra.     D(x·y², x) = y²,  D(x·y², y) = 2·x·y.  Entrambe le derivate sono nulle quando (x, y) = (0, 0).  Ma, come si vede nella figura, in (0,0) non c'è né un massimo né un minimo.  È comunque un punto stazionario, ossia è un punto tale che se una bilia fosse collocata sulla superficie esattamente in tale punto essa rimarrebbe ferma.     Un punto stazionario può essere di massimo relativo o di minimo relativo o, come questo, di sella (detti così perché anche il centro di una sella è un punto a tangente orizzontale pur non essendo di massimo o di minimo).  I punti di sella corrispondono ai punti di flesso del caso univariato.

2

Dai grafici all'inizio del paragrafo cerca di dedurre quanto valgono le derivate rispetto ad x e rispetto ad y di F in (3, 0) e controlla la risposta calcolandole. È un punto di massimo, di minimo o di sella?

4. Altri esempi. La continuità.

    Consideriamo F(x,y) = sin(x) + cos(2 y) di cui nel §1 abbiamo già tracciato il grafico.  ∂ sin(x) + cos(2 y) / ∂x = cos(x),  ∂ sin(x) + cos(2 y) / ∂y = −2·sin(2 y).  Si annullano entrambe le derivate prime per  x = π/2 + k·π  e per  2y = k·π, ovvero  y = k·π/2,  al variare di k tra i numeri interi.
    Il grafico ha infinite gobbe.  Nel punto  (π/2,π)  (segnato in figura) e in (π/2,0), (π/2,-π), (-3π/2,−π), ... F vale  sin(π/2)+cos(2·π) = 1+1 = 2.  È il valore massimo. Lo raggiunge in generale in  (π/2+hπ, kπ)  al variare di h e k tra i numeri interi.

    Analogamente nei punti   (−π/2,−3π/2)  (segnato), (−π/2,−π/2), (−π/2,π/2) e in generale in  (−π/2+hπ, −π/2+kπ)  (al variare di h e k tra i numeri interi) assume il valore minimo.

    Negli altri punti in cui si annullano le derivate prime,  come in (−π/2, π) (segnato in figura), in (−π/2, 0), ...  vi sono dei punti di sella.

    Nel caso univariato i punti di massimo e di minimo possono cadere anche agli estremi del dominio (ad es. se questo è un intervallo [a, b] chiuso e limitato) o in punti in cui la funzione non è derivabile (x → |x| ha un minimo in 0 dove non esiste la derivata prima).  Analogamente, nel caso bivariato vi può essere un punto di minimo o di massimo o agli estremi del dominio o in un punto in cui non esistono entrambe le derivate parziali.

    Non si è data la definizione di continuità per le funzioni di 2 variabili: è analoga a quella del caso univariato.

    Premettiamo che se F è a 2 input e 1 output e Q è un punto interno al dominio (o sul suo bordo), lim _{P → Q} F(P) = L quando per ogni ε>0 esiste δ tale che |F(P)−L| < ε se la distanza tra P e Q è minore di δ;  se Q sta nel dominio di F e L = F(Q) si dice che F è continua in Q. 
    Ma c'è una differenza rispetto al caso univariato:  F può avere in un punto del suo dominio tutte le derivate parziali del 1º ordine senza essere ivi continua. Ad esempio nel caso illustrato sotto F vale 0 in (0,0) e altrove 2·x·y/(x²+y²):  non ha limite in (0,0) mentre ivi le sue derivate parziali rispetto sia a x che a y valgono 0 (verificalo).

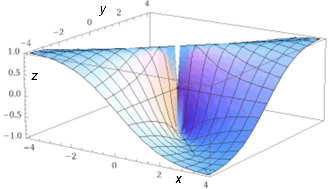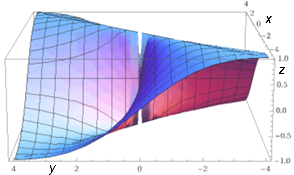plot z=2*x*y/(x^2+y^2), x from -4 to 4, y from -4 to 4, z from -1 to 1 view from(4,-6,2)
plot z=2*x*y/(x^2+y^2), x from -4 to 4, y from -4 to 4, z from -1 to 1 view from(-4,0,1)

3      Sia G la funzione  (x,y) → √(x² + y²)  ristretta al dominio costituito dal cerchio del piano x,y centrato in (0,0) e di raggio 4.  Il suo grafico è il cono che va dal vertice (0,0,0) al cerchio di raggio 4 alla quota 4 con centro in (0,0,4).    Quali sono i punti di minimo e quelli di massimo di G?  Si possono calcolare in essi le derivate?  Valgono zero?            Come è stato tracciato il grafico: plot z = 2*x*y/(x^2+y^2), x from -4 to 4, y from -4 to 4, z from -1 to 1 view from(-4,0,1)

4

Sotto è tracciato il grafico della funzione  H: (x,y) → −x³.  Individuane i punti stazionari, specificandone il tipo.

plot z = -x^3, x from -3 to 3, y from -3 to 3, z from -20 to 20 view from(4,2,1.5)

5. L'hessiano

    Abbiamo visto (qui) come lo studio della derivata seconda possa essere utile per determinare la natura dei punti in cui si azzera la derivata prima.  Analogamente lo studio delle derivate seconde di una funzione di due variabili può essere di aiuto per determinare la natura dei punti in cui si azzerano le derivate prime.  Accenniamo, senza dimostrazioni, a questi aspetti, lasciandone l'approfondimento a chi proseguirà gli studi in ambito scientifico.

    Le derivate parziali del secondo ordine sono, semplicemente, le derivate parziali delle derivate parziali. Ecco qualche esempio di calcolo con WolframAlpha:

d/dx x*y^2  y^2       d/dx d/dx x*y^2  0       d/dx d/dy x*y^2  2*y
d/dy x*y^2  2*x*y     d/dy d/dx x*y^2  2*y     d/dy d/dy x*y^2  2*x

    Si noti che la derivata seconda rispetto ad x e ad y coincide con quella rispetto ad y e ad x.

    Usualmente si scrive  ∂² (x·y²) / (∂x ∂y)  o  F_xy(x,y)  se  F(x,y) = x·y².

    Data F funzione di due variabili, chiamiamo  F_xx(x,y)·F_yy(x,y) − F_xy(x,y)·F_yx(x,y), che equivale a  F_xx(x,y)·F_yy(x,y) − F_xy(x,y)²,  hessiano di F.  Indichiamolo  H _F (x,y).

    Supponiamo che F abbia derivate seconde continue e che (x,y) sia un punto stazionario. Allora:
•  se H _F (x,y) < 0  (x,y) è un punto di sella;
•  se H _F (x,y) > 0  (x,y) è un punto di minimo o di massimo (locale) a seconda che F_xx(x,y) sia positivo o negativo;
•  se H _F (x,y) = 0  non si può concludere nulla.

    Nel caso di  F(x,y) = sin(x) + cos(2 y)  abbiamo H_F(x,y) = −sin(x)·(−4·cos(2y)) − 0 = 4·sin(x)·cos(2y).  In (−π/2,0), che è un punto stazionario, H_F(−π/2,0) = −4 < 0, quindi (−π/2,0) è un punto di sella, in accordo con quanto avevamo già concluso nel §4.  Con WolframAlpha:

Hessian ( sin(x)+cos(2*y) )      4*sin(x)*cos(2*y)

6. Esercizi

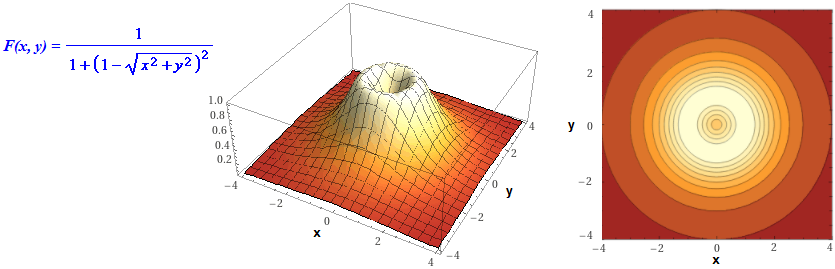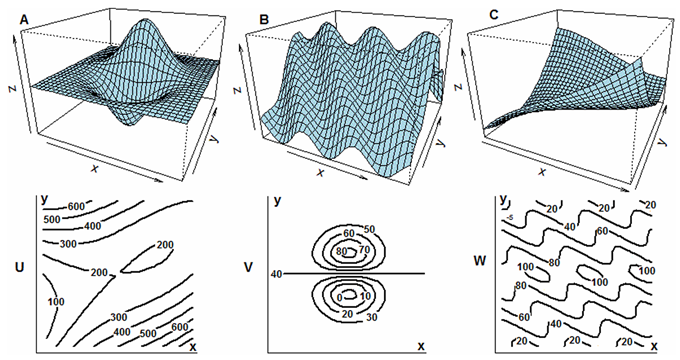
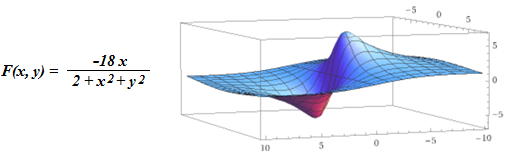
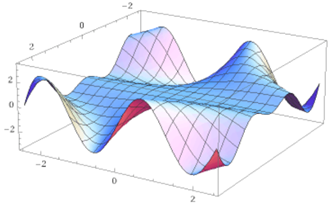e1      Trova il minimo della funzione F, avente come dominio R×R, così definita:  F(x, y) = (x − y)4 + y4

e2      Considera la funzione F definita sotto e la sua rappresentazione grafica, ristretta al dominio [−4,4]×[−4,4], che ha una forma di cratere.  Quanto è profondo il "cratere", cioè quanto differiscono la quota del bordo del cratere dalla quota del suo punto più basso?            Grafico tracciato con: plot z =1/(1+(1-sqrt(x^2+y^2))^2), x from -4 to 4, y from -4 to 4, z from 0 to 1 view from(10,4,8)

e3      Sotto sono raffigurate tre porzioni (inventate) di superficie terrestre. Le superficie C nella parte centrale, che non si vede, ha un avvallamento. Con x ed y si sono indicate latitudine e longitudine, con z la quota.  Associa ad ognuna di queste porzioni la corrispondente carta delle curve di livello.  Motiva le risposte.

e4      Studia, graficamente e simbolicamente, aiutandoti col computer, la seguente funzione, il cui grafico è stato ottenuto coi comandi:         plot z =-18*x/(2+x^2+y^2), x from -10 to 10, y from -8 to 8, z from -7 to 7 view from(4,10,1)

e5      Completa il comando seguente per ottenere, col computer, una rappresentazione grafica di  (x,y) → sin(x·y)  simile a quella a lato e determina che tipo di punto critico è (0,0):         plot z =sin(x*y), x from ... to ..., y from ... to ..., z from ... to ... view from(...,...,...)

e6      Data F: (x,y) → sin(x·y), scrivi la funzione di una variabile G: R → R che si ottiene tagliandone il grafico col piano y = x e tracciane il grafico, aiutandoti col computer.  Confronta il grafico ottenuto con quello di F.