da: Notiziario dell'Unione Matematica Italiana, 1984, n.1
INDAGINE SULLE
CONOSCENZE MATEMATICHE DELLE MATRICOLE
DI CORSI DI
LAUREA IN MATERIE SCIENTIFICHE
Giuseppe Accascina (Dipartimento di Matematica, Università di Pisa)
Carlo Dapueto (Istituto di Matematica, Università di Genova)
Introduzione
Riportiamo i risultati di un'indagine, effettuata per mezzo di un
questionario distribuito negli A.A. 1982-83 e 83-84 alle matricole di
alcuni corsi di laurea delle Università di Genova e di Pisa,
per verificare il livello di preparazione matematica degli studenti
all'ingresso all'Università.
Il questionario è
stato redatto dalla commissione didattica dell'Istituto di Matematica
dell'Università di Genova. Per la sua formulazione si è
fatto riferimento al "Syllabus di Matematica" (vedere
N.U.M.I., n.3, 1980). I questionari sono stati distribuiti, compilati
e restituiti nella prima ora accademica di lezione.
Il questionario è
di tipo aperto; esso è stato preferito a quello a risposte
predeterminate per avere la possibilità di analizzare i
procedimenti logici e le procedure e di risoluzione usate dagli
studenti. Ciò ha permesso di svolgere una dettagliata analisi
qualitativa delle risposte fornite ai singoli quesiti.
Riportiamo di
seguito una tabella sinottica dei questionari esaminati suddivisi per
scuola di provenienza, sede e corso di laurea (accorpati per
affinità) ed il testo del questionario.
Tabella 1 - Questionari esaminati
Corso di laurea di iscrizione Scuola di provenienza
L.Sc. L.Cl. I.T.I. Altre Totale
MATEMATICA Mat., GE (1) 162 36 9 50 257
E Mat., PI (2) 36 4 3 6 49
INFORMATICA Inf., PI (3) 91 15 18 33 157
totale 289 55 30 89 463
FISICA GE (4) 27 9 7 8 51
PI (2) 60 22 11 7 100
totale 87 37 78 75 757
INGEGNERIA GE (5) 127 20 64 32 243
PI (6) 119 31 60 23 233
totale 246 51 724 55 476
GEOLOGIA Geo., GE (4) 42 9 3 17 71
E Bio., GE (7) 18 19 4 20 61
BIOLOGIA Bio., PI (8) 40 7 0 14 61
totale 100 35 7 57 793
T0TALE 722 172 779 270(9) 7283 |
(1) A.A. 1982-83 e 83-84; (2) A.A. 1983-84; (3) A.A. 1983-84, uno dei 4 corsi; (4) A.A. 1982-83; (5) A.A. 1982-83 e 83-84, ing. mecc. e chim.; (6) A.A. 1983-84, ing. elettronica e elettrotecn.;(7) A.A. 1982-83, uno dei 2 corsi; (8) A.A. 1983-84, uno dei 2 corsi; (9) di cui: Mag. 41, L.Ling. 8, L.Art. 4, I.T.Comm. e Geom. 75, Prof. 23, Nautico 19, Scuole straniere 9, non specificato 31.
Testo del
questionario
1) Dal fatto che 6 è
divisore di a·b si può dedurre che 6 è divisore di a
oppure di b? (a e b sono numeri interi; motivare la risposta).
2) Nel paese A il
costo della vita è aumentato del 10% nel primo semestre del
1982 e del 10% nel secondo semestre. Di quanto è aumentato nel
1982?
3) Risolvere
l'equazione (2x-1)(2x+1)(3x+1) = 0
4) Mettere in ordine
di grandezza i seguenti numeri (specificando quali sono eventualmente
uguali):
1 — -100 — -100 -100
2 - —————— ; 1,9 (= 1,999...); 2 - 10 ; 0,3*6 ; 2 ; 2 ; 2 - 1
100
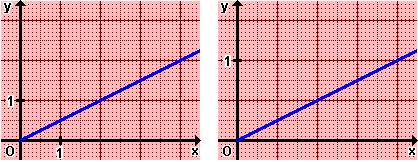
105) Fissare l'unità di misura sull'asse x del secondo grafico in modo che i due grafici rappresentino la stessa funzione.

3
6) Data l'equazione 2x+3 = 0, perché x = - — è soluzione?
2
7) Di un rettangolo
R si conoscono le misure della base a e dell'altezza b, a = 0,8 cm e
b = 0,9 cm, con la precisione di un millimetro (cioè si sa che
le misure di a e di b possono differire dai valori indicati per
eccesso o per difetto al più di 1 mm). Si cancellino con una
barra tra i seguenti valori quelli che sicuramente non possono
essere l'area di R.
1 cm2; 0,6 cm2; 0,4
cm2; 0,8 cm2; 0,5 cm2; 0,7 cm2
8) Se a e b sono
due numeri interi relativi non nulli (...,-3,-2,-1,1,2,3,...) quando
si ha a/b > 0?
Analisi delle
risposte
Per poter
innanzitutto effettuare una sintesi quantitativa del grado di
conoscenza degli studenti distinguendo per scuola di provenienza e
per corso di laurea di iscrizione, si sono stabiliti dei criteri in
base ai quali considerare una risposta "esatta" o "errata".
In particolare nel
terzo quesito si è inteso per risposta "esatta" una
risposta corretta senza aver moltiplicato i polinomi di primo grado.
Nel quarto quesito
solo una piccola minoranza (circa il 2%) ha saputo ordinare
correttamente tutti i numeri. Per questo (al fine di ottenere un
parametro significativo) si sono considerate risposte "esatte"
quelle in cui sono sono stati messi nell'ordine giusto i termini
2-100, 2-1-100, 2-1/10100 e
1,999....
Nel sesto quesito si
è considerata risposta "esatta" ogni risposta del
tipo: "poiché sostituendo... l'uguaglianza risulta essere
vera" (o "poiché verifica l'equazione").
Riportiamo di
seguito due tabelle da cui si desume il diverso livello di
preparazione degli studenti a seconda della scuola di provenienza e
del corso di laurea di iscrizione (ricordiamo che il numero dei
quesiti è 8).
Tabella 2 - Numero medio di risposte "esatte" per corso di laurea
Matematica e Informatica 4,7
Fisica 5,9
Ingegneria 4,8
Geologia e Biologia 3,1
Totalità studenti 4,6 |
Tabella 3 - Numero medio di risposte "esatte" per provenienza
Liceo scientifico 5,0
Liceo classico 4,2
I.T.I. 4,5
Altre 3,7
Totalità studenti 4,6 |
Si nota un basso
numero di risposte esatte; risultato che si manifesta ancora più
preoccupante se si tiene presente che si tratta di studenti che, per
la scelta del corso di laurea, sono da considerarsi i più
interessati e presumibilmente i più "portati" alla
matematica.
Una prima analisi
della tabella 2 sembra mostrare un'autoselezione da parte degli
studenti all'atto dell'iscrizione. Infatti gli studenti di Fisica
hanno risposto meglio dei loro colleghi; una spiegazione potrebbe
essere ricercata nella consapevolezza di dover affrontare un corso di
laurea più impegnativo. La situazione opposta invece si
riscontra per gli studenti di Geologia e Biologia, corsi di laurea in
cui si richiede un minor impegno matematico.
Non si nota (vedere
tabella 3) una grande differenza di preparazione tra gli studenti
provenienti dai diversi tipi di scuola. Interessanti differenze si
deducono invece dall'esame della tabella che segue.
Tabella 4
Percentuali di risposte "esatte" ai singoli quesiti per provenienza
Quesiti 1 2 3 4 5 6 7 8
———————————————————————————————————————————————————————————————————
Liceo scientifico 35 60 76 40 90 67 47 87
Liceo classico 35 52 51 28 88 61 40 65
I.T.I. 5 62 58 35 87 63 50 79
Altre 20 40 40 21 74 46 30 59
Totalità studenti 31 56 64 34 86 62 43 78 |
Notiamo che l'ordine
di difficoltà incontrata dagli studenti è indipendente
dalla scuola di provenienza; ad esempio la domanda n.5 è
risultata la più facile, mentre la n.l la più
difficile. Restringendo l'analisi al confronto tra gli studenti
provenienti dal liceo scientifico, dal classico e dall'I.T.I., si
nota che:
gli studenti del
liceo scientifico si dimostrano più preparati dei loro
colleghi nelle disequazioni (quesito 8) e nella risoluzione di
equazioni algebriche (ques. 3);
gli studenti del
classico hanno più difficoltà dei loro colleghi nelle
disequazioni (ques. 8) e nell'uso delle potenze (ques. 4);
gli studenti
dell'I.T.I. rispondono meglio dei loro colleghi ai quesiti di tipo
applicativo. quali il calcolo del costo della vita (ques. 2) e
dell'area del rettangolo (ques. 7); mostrano invece notevoli
difficoltà nella risoluzione dell'esercizio teorico di tipo
aritmetico (ques. 1).
Le stesse tabelle
sono state elaborate separatamente per gli studenti di Genova e di
Pisa. le linee di tendenza risultano invariate. Si nota però
che il numero medio delle risposte esatte degli studenti di Pisa è
maggiore di quasi mezza risposta al numero medio calcolato sulla
totalità degli studenti. Fattori che possono aver contribuito
a determinare questo scarto sono il fatto che agli studenti di molte
scuole toscane viene distribuito il "Syllabus" e il fatto
che a Genova il questionario è stato distribuito in quattro
versioni diverse nell'ordinamento delle domande, il che può
aver reso più difficoltosa la copiatura.
Commento alle
risposte ai singoli quesiti.
Quesito 1
Sono state
considerate "esatte" oltre alle risposte "no" in
cui è stato mostrato un controesempio o è stata svolta
un'argomentazione corretta ed esauriente (come: "6=2·3, quindi
affinché a·b sia divisibile per 6 basta che a sia divisibile
per 2 e b sia divisibile per 3"), anche quelle in cui la
motivazione non è stata svolta completamente (es. "poiché
a e b possono essere sottomultipli di 6" o "poiché 6
non è primo"). Nonostante ciò il quesito 1 è
quello che ha ottenuto il minor numero di risposte "esatte".
Le altre risposte
"no" (circa 1/4 del totale) non contenevano motivazioni o
contenevano motivazioni errate o tautologiche (es. : "6 è
divisore di a o di b se a o b è multiplo di 6").
Tra coloro che hanno
risposto "sì" la maggioranza ha dato motivazioni (qui riportate usando
una scrittura a "1 piano", senza ricorrere a "linee di frazione") del
tipo "infatti a·b/6 = a/6·b o a·b/6 = a·(b/6)", alcuni hanno
precisato che "a o b deve essere 6" e molti (circa 1/4)
hanno precisato che 6 deve essere divisore sia di a che di b, in
genere basandosi sull'"eguaglianza": a·b/6 = a/6·(b/6)
(diversi di questi invero hanno risposto "no" al quesito,
facendo seguire la "spiegazione" che deve essere divisore
di entrambi i numeri, mostrando così di non aver neanche
compreso la "logica" della domanda).
Quesito
2
Sono state
considerate "esatte" oltre alle risposte "21%"
anche quelle in cui è stato solo abbozzato il procedimento per
ottenere la soluzione (es. "se x è il costo della vita si
ha (x+10%x)+l0%(x+10%x)"). Le risposte "esatte"
nella grande maggioranza contengono solo la soluzione "21%"
senza procedimenti di calcolo e spesso presentano la cancellatura di
altre soluzioni; alcune contengono l'osservazione che se ci si
riferisce all'inizio del secondo semestre invece che all'inizio
dell'anno l'aumento e del 20% (!).
Tra coloro che hanno
sbagliato i più hanno risposto "20%" (circa la metà)
e "l0%"; seguono in ordine di frequenza le risposte: "11%"
(ottenuto in genere così: 10%+10%10% = 11%), "30%"
(l0%+20%=30%) , "15%" ((l0%+20%)/2) , "0,21%",
"12,1%", "20,1%" "22%", "più
del 20%", "15,1%", "più del 21%",
"31%", "12%", "10,5%", "19%",
"circa 19,1%", "5%", "7%", "48,4%",
"100%",... E poi dicono che l'insegnamento della matematica
nelle scuole superiori stimola poco la capacità di
"astrazione" (dai calcoli economici presenti
quotidianamente sui giornali ...) e la "creatività"
(trovare così tanti valori diversi, persino inferiori a 10%
...)!
Quesito 3
Sono state
considerate "esatte" sia le risposte in cui le soluzioni
sono accompagnate da una traccia del procedimento sia quelle
contenenti solo le soluzioni. Tra le risposte "esatte"
circa un quarto presentano le soluzioni a fianco della cancellatura
di tentativi di ricerca delle radici di un polinomio di 3° grado.
Negli altri
questionari in cui sono state ottenute le soluzioni corrette (circa
1/5) si è proceduto moltiplicando i primi due binomi ( (4x2-l)(3x+l)=0; x=±1/2, x=-1/3 ) oppure
moltiplicando tutti i binomi, trovando poi una soluzione mediante la
"regola di Ruffini" o raccoglimenti a fattor comune e
risolvendo infine la rimanente equazione di 2° grado.
Nei restanti
questionari o non sono state trovate soluzioni (i più dopo
aver moltiplicato i binomi hanno dichiarato di non saper risolvere le
equazioni di 3° grado; molti hanno sbagliato la moltiplicazione,
anche ottenendo polinomi di grado diverso dal 3°, altri hanno
intrapreso errati raccoglimenti a fattor comune) o sono state trovate
solo alcune soluzioni (molti non hanno trovato -1/2 poiché da
x2-1/4=0 hanno ricavato solo x=1/2; alcuni hanno
"semplificato" per 3x+1 e hanno ottenuto solo x=±1/2) o
sono state date soluzioni che non erano tali (x=0; x≠1/2, x≠-1/2, x≠-1/3 ; x>-l/3, procedendo con "Tartinville";
...)
Quesito 4
Circa il 2% - come
già ricordato - ha ordinato correttamente tutti i numeri. Le
risposte "esatte", cioè quelle in cui sono stati
messi nell'ordine giusto 2-100, 2-1-100,
2-1/10100 e 1,999..., sono state solo il 34% (e tra queste
diverse si sono esplicitamente basate su considerazioni del tipo
2-100 = 0,02 e 2-1-100 = 1,99).
Analizzando più
in dettaglio le risposte, osserviamo che nella grande maggioranza
(circa 3/4) dei questionari sono stati indicati come eguali 2-1/10100
e 2-10-100; meno (circa la metà del totale) sono
sia quelli in cui è stato indicato che 2-100 è
più piccolo di tutti gli altri numeri sia quelli in cui
2-1-100
è stato considerato inferiore a 2-1/10100.
Questo scarto mette
in luce la difficoltà a leggere e usare le potenze al di fuori
di esercizi standard (un esempio significativo è dato dalla
"trappola" in cui è cascato chi da 1<10 ha
dedotto che 1-100 è inferiore a 10-100).
Meno della metà sono i questionari in cui 2-1/10100 è
stato considerato inferiore a 1,999... : è evidente dietro a questo
fenomeno l'uso acritico delle calcolatrici tascabili, utilizzando le
quali si ottiene 2-1/10100 = 2.
Ammontano circa al
10% sia coloro che hanno indicato come eguali 1,999... e 0,333...·6
(eguaglianza intuibile anche con la calcolatrice: 0,3333333·6 =
1,9999998) sia coloro che hanno indicato come eguali 0,333...·6 e 2
(pensando a 0,333... come 1/3 e/o battendo sulla calcolatrice
[1][:][3][x][6][=]); molto meno (circa il 2%,
pochi questionari in più di quelli in cui sono stati ordinati
correttamente tutti i termini) sono i questionari in cui 1,999... e 2 sono
indicati come eguali; questi questionari costituiscono in pratica
l'intersezione di quelli in cui è stato posto 1,999... = 0,333...·6 e
quelli in cui è stato posto 0,333...·6 = 2 (per cui si può
supporre che in genere l'eguaglianza tra 1,999... e 2 sia stata
individuata indirettamente per transitività).
Le difficoltà
incontrate nel confronto tra 2, 0,333...·6 e 1,999... segnalano grosse
lacune nella preparazione numerica, sia a livello concettuale
(concetto di numero reale, concetto di limite, ...) sia a livello
operativo (approssimazione,... ; la giustamente dimenticata regoletta
per trovare istantaneamente" la "frazione generatrice"
di un qualunque numero periodico non è stata rimpiazzata da
altre conoscenze e abilità).
Per brevità
non riportiamo classificazioni ed esempi degli assai vari tipi di
errore, che vanno dalle relazioni d'ordine più bizzarre, come
quelle in cui 2-10-100 o 2-1-100 è
maggiore di 2 ("-" e "-" fa "+"!), ai
calcoli più strani, come 0,333·6 = 1,888... (si fa il prodotto di 0.3·6 senza
"—" sopra "3" e poi si riporta "—", sopra a 8, nel risultato).
Quesito 5
E' quello che ha
avuto il maggior numero di risposte esatte, tuttavia tra i pochi che
hanno anche motivato la risposta "esatta" i più
hanno dato spiegazioni errate (la più comune è stata
del tipo: y = 1/2 x, y=1
La risposta
sbagliata più diffusa è stata quella di fissare l'unita
sull'asse x a 4 cm dall'origine; seguono, in ordine di frequenza,
quelle in cui viene fissata a 0,5 cm e quelle in cui viene fissata a
1 cm. E poi: chi pone 1 a 3 cm, chi pone 1/2 a 4 cm, chi pone 1 a
1/4 cm, chi afferma che si può mettere 1 ovunque, chi fissa le
unità su entrambi gli assi come nel primo grafico, ...
Quesito 6
La valutazione se le
varie risposte rientrano nella fissata categoria convenzionale di
risposta "esatta" si è leggermente differenziata tra
le persone che hanno fatto lo spoglio dei questionari a seconda del
rilievo dato alla correttezza linguistica; da tutti sono state
considerate "esatte" oltre alle risposte del tipo: "poiché
2(-3/2)+3=-3+3=0", "poiché sostituendo ...
l'eguaglianza risulta essere vera", "poiché -3/2
soddisfa l'equazione", ... anche: "la funzione si
annulla", "sostituendo si ottiene come risultato zero"
,...
Alcuni hanno
considerato "esatte" anche le risposte del tipo "perché
è il valore da dare a x affinché la equazione risulti
uguale a zero", "perché rende valida l'identità
2x+3=0", "poiché verifica la funzione",... in
cui si è intuita la motivazione "esatta", ma si sono
usati scorrettamente i termini "equazione", "funzione",
"identità", ...
Sono state
considerate "esatte" anche tutte le risposte in cui alla
risoluzione dell'equazione è stata fatta seguire la verifica
(spesso effettuata ricorrendo meccanicamente alla somma di frazioni:
2·(-3/2)+3 = -6/2+3 = (-6+6)/2 = 0).
Nella maggioranza
dei questionari con risposta non "esatta" è stata solamente
risolta l'equazione; altri hanno tentato di spiegare (e motivare)
come si risolvono le equazioni di primo grado (da "perché
la formula risolutiva è x=b/a" a "perché si
applicano le proprietà dell'algebra", "si isola la x
e si trasportano i numeri che assumono valori negativi" e altre
"spiegazioni" più elaborate).
Altri ancora hanno
dato risposte diverse: "perché -3/2 ≠ 0", "perché
x è il punto della retta che tale funzione rappresenta",
"perché, data una funzione rappresentabile con una retta,
il punto di ascissa x=-3/2 fa parte della funzione".
Quesito 7
Tra le risposte
esatte solo una piccola minoranza presenta tracce di una motivazione
corretta (cioè: 0,56 cm2 < area di R < 0,9
cm2), la maggioranza non contiene motivazioni e in diverse
si osserva che l'area di R deve essere compresa tra 0,72 cm2 -
1 mm2 e 0,72 cm + 1 mm2 e si deduce da ciò
che sono da scartare i valori non compresi tra 0,6 cm2 e
0,8 cm2; questa motivazione doppiamente errata (sia nella
determinazione della precisione del prodotto che nella somma di
grandezze espresse in unità diverse) è probabilmente
implicita in molte delle risposte esatte che non sono state frutto di
sola copiatura.
Naturalmente, le
altre risposte più diffuse sono state quelle in cui si è
accettato solo il valore 0,7 cm2 e quella in cui si sono
accettati 0,7 cm2 e 0,8 cm2 (0,72 è
compreso tra 0,7 e 0,8!); segue in ordine di frequenza la risposta in
cui vengono barrati tutti i valori (0,72 cm2 non compare
tra i valori indicati!); altre risposte frequenti sono state quella
in cui sono scartati solo i valori estremi, 1 cm2 e 0,4
cm2, e quella in cui si è accettato solo 0,4 cm2
(questa risposta deriva - come appare evidente in alcuni questionari
- dall'uso della formula per il calcolo dell'area del triangolo:
0,8·0,9/2 = 0,36, che è circa 0,4).
Vi sono poi molte
altre risposte, da quelle "contradditorie" (in cui si
accettano due valori e non un valore tra essi compreso) a quella in
cui si dichiara che tutti i valori sono accettabili,... fino a
totalizzare una trentina di risposte diverse. Alcuni aggiungono: "non
sono sicuro della risposta poiché non ho con me la
calcolatrice"!
Quesito 8
Sono state
considerate "esatte" anche le numerose risposte in cui la
soluzione è formulata scorrettamente (es.: "a>0 U
b>0", "∀a o ∀b sono concordi", "entrambi
+ o entrambi -", "... poiché (a>0)/(b>0)>0
e (a<0)/(b<0)>0", ... e anche:"a e b di segno
concorde", "sia a che b entrambi dello stesso segno",
...); molti aggiungono "e b≠0".
Nella maggioranza
degli altri questionari viene considerata la relazione d'ordine che
intercorre tra a e b. La risposta più frequente è
"a>b"; seguono "a e b concordi e a>b",
"a>b>0 o 0>b>a", "a e b concordi o a>b",
"a e b concordi e |a|>|b|", "a>b>0", e
analoghe con ">" invece di ">"; altre
risposte sono: "a≥b" o b>0", "a≥b e a>0",
"a>b o a>-b", "a b", "a>ab",
"a>b>0 o a<b<0 o b>a>0", ...
b", "a>ab",
"a>b>0 o a<b<0 o b>a>0", ...
In altri questionari
viene considerata la relazione di divisibilità tra a e b: "a
multiplo di b", "concordi e a multiplo di b",
"concordi o a multiplo di b", ...
Poi vi sono risposte
del tipo: "a>0 e b>0 (o "a U b > 0", ...),
"a>0 o b>0", "a<0 e b<0", "a>0
e b>0", "(a>0 e b<0) o (a<0 e b>0)",
"a>0", "a≠0≠b", "b≠0",
"b≥0", "b≠1", "a=0", "prendendo
|a| e |b|", ... , "mai", "sempre".
Vi sono risposte che
manifestano assoluta non padronanza dell'uso delle lettere: "+a/+b
o
Osserviamo infine
che oltre ad esservi numerose risposte sintatticamente scorrette (sia
nell'uso di simboli matematici che nell'uso della lingua italiana) vi
sono anche numerose risposte in cui difetta la "logica"
(sia come raziocinio" che come padronanza della semantica delle
costruzioni della lingua italiana): dalle risposte contenenti
contraddizioni (come "a>0, b>a, b<0") a quelle
contenenti tautologie (come "a e b concordi o discordi" o "
se |a|-|b|<|a|+|b|") o tautologiche rispetto al quesito ("se
a·b>0"), da quelle espresse in modo ridondante (come "a>b>0
o 0<b<a", "-a>b o a<-b", "a>b,
b>0, a>0", ... o come "concordi e a>0") a
tutte le risposte in cui si fa un uso promiscuo di "e" e
"o".
Considerazioni
conclusive.
Ci siamo soffermati
a commentare abbastanza in dettaglio le risposte ai vari quesiti
perché ci è sembrato utile fornire un quadro abbastanza
analitico delle carenze dell'insegnamento matematico nell'attuale
scuola superiore, sia in vista di una riformulazione dei programmi
scolastici nell'ambito della (eventuale?) riforma della scuola
secondaria superiore, sia pensando che le informazioni sui livelli di
ingresso all'Università possano servire per ripensare
all'impostazione dei corsi universitari del primo anno.
Da questo punto di
vista ci sembra che l'analisi condotta, nonostante i limiti
(difficoltà a valutare e classificare precisamente le
risposte, limitatezza geografica del campione, presenza di numerose
risposte "copiate",...), abbia fornito indicazioni assai
utili.
Riteniamo che,
basandosi sui risultati di questa indagine, sia possibile realizzare,
mediante un nuovo questionario, un'ulteriore indagine, che permetta
di effettuare anche valutazioni e confronti su scala nazionale. Gli
interessati a una simile iniziativa sono pregati di mettersi in
contatto con Giuseppe Accascina (Dipartimento di Matematica
dell'Università di Pisa) o con Carlo Dapueto (Istituto di
Matematica dell'Università di Genova).