 |
 |
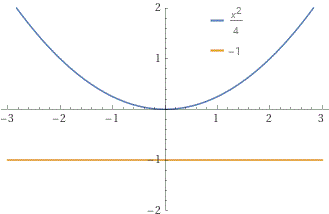
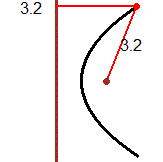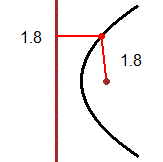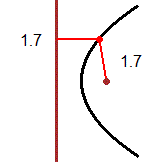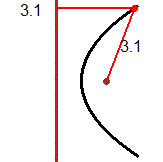
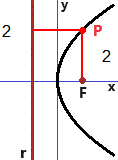
La parabola sopra riprodotta a sinistra, posso descriverla analiticamente come x = a·y² pensando che l'asse x passi per il punto segnato (il "fuoco" della parabola) e l'asse y sia tangente alla parabola, come si vede nella seconda figura. Se consideriamo il punto P nella seconda figura, tenendo conto che xP = 1, yP = 2, da 1 = a·4, ricavo a = 1/4. Dunque la parabola ha equazione x = y^2/4.
Ma se non sapessi che la curva generata dal punto che si muove nel modo descritto ha equazione
x = a·y², potrei descrivere la curva con l'equazione che esprime il fatto che la distanza di P da r
è uguale a quella di P da F:
Se esplicito x in funzione di y ottendo proprio x = y^2/4:
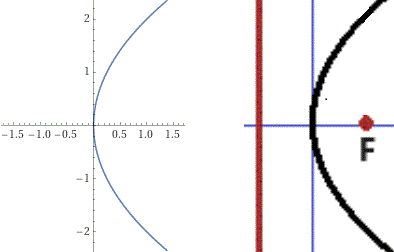
Se traccio y = x^2/4 con WolframAlpha (tenendo conto che tracciando i grafici di funzione con WolframAlpha
si ottiene una scala monometrica se larghezza = 1.5*altezza, ovvero: altezza = 2/3*larghezza) col comando