Velocità di variazione
 Il grafico che segue rappresenta una funzione interessante: la temperatura al variare del tempo rilevata alla stazione meteo di Sassello (paese ad 800 m di altitudine, in provincia di Savona), nei primi 8 giorni del febbraio del 2012. Abbiamo riportato solo i valori registrati ogni 3 ore. [qui lo script in cui puoi recuperare i dati]
Il grafico che segue rappresenta una funzione interessante: la temperatura al variare del tempo rilevata alla stazione meteo di Sassello (paese ad 800 m di altitudine, in provincia di Savona), nei primi 8 giorni del febbraio del 2012. Abbiamo riportato solo i valori registrati ogni 3 ore. [qui lo script in cui puoi recuperare i dati]
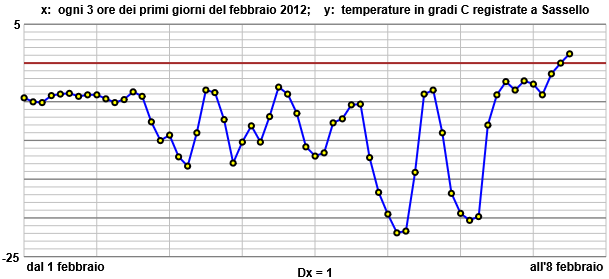
Vediamo che c'è stato un periodo di circa 1 giorno e mezzo (36 ore) durante il quale la temperatura non è praticamente cambiata (ha oscillato tra i -5 e i -4 gradi). Ci sono stati poi periodi caratterizzati da brusche variazioni di temperatura: drastiche diminuzioni, seguite da improvvisi aumenti. Il 6 febbraio c'è stato l'intervallo di 6 ore in cui la temperatura è cresciuta più rapidamente:
è passata circa da -22° a -4°, aumentando di 18°, ossia con una velocità media di crescita di
18/6 = 3°/h.
|
 A destra un'altra immagine: mostra come è cambiata la temperatura di un termometro che abbiamo tolto da una pentola di acqua calda, lasciandolo poi raffreddare a contatto con l'ambiente esterno. Vediamo che la temperatura è andata sempre diminuendo: più rapidamente all'inizio, poi via via più lentamente al passare dei secondi. [qui lo script in cui puoi recuperare i dati]
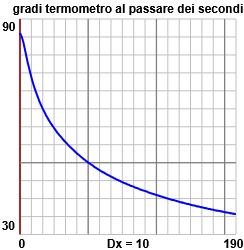
A destra un'altra immagine: mostra come è cambiata la temperatura di un termometro che abbiamo tolto da una pentola di acqua calda, lasciandolo poi raffreddare a contatto con l'ambiente esterno. Vediamo che la temperatura è andata sempre diminuendo: più rapidamente all'inizio, poi via via più lentamente al passare dei secondi. [qui lo script in cui puoi recuperare i dati]
Di quanto è variata la temperatura nei primi 10 s? Di -10°
E nel primo minuto? Di -35°
E nel terzo? Di -5°
Le velocità medie di variazione erano di -10°/(10 s) = -1 °/s,
-35°/(60 s) = -0.58 °/s, -5°/(60 s) = -0.083 °/s
| |  |
 La velocità di variazione può essere valutata anche non rispetto al tempo. Un esempio.
La velocità di variazione può essere valutata anche non rispetto al tempo. Un esempio.
Riempo con del liquido la piccola cisterna fatta "a scalini" raffigurata sotto, dove le dimensioni sono indicate in cm. Vediamo come varia il livello h (in cm) all'aumentare del volume V (in litri) del liquido immesso:
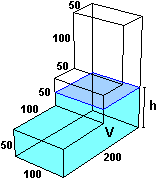 |
– inizialmente il livello cresce proporzionalmente al volume;
– quando si raggiunge il livello 50 la sezione del recipiente si riduce per cui dopo h cresce più rapidamente (la sezione si dimezza per cui il liquido si innalzerà con velocità doppia);
– arrivati al livello 100 la sezione si riduce ulteriormente per cui la velocità con cui varia h aumenta ancora.
Per tracciare il grafico tengo conto che al livello 50 cm il volume è 100·200·50 cm³ = 1000 litri, per cui il primo tratto rettilineo arriva nel punto (1000,50). Al livello 100 cm si sono aggiunti 100·100·50 cm³ = 500 litri di liquido: il secondo tratto termina in (1500,100). Al livello 200 se ne sono aggiunti 100·50·100 cm³ = 500 litri: il terzo tratto termina in (2000,200). Abbiamo il grafico sotto a sinistra. | 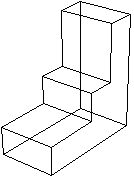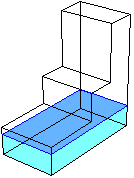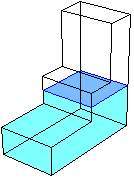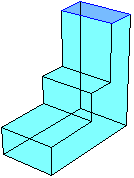 |
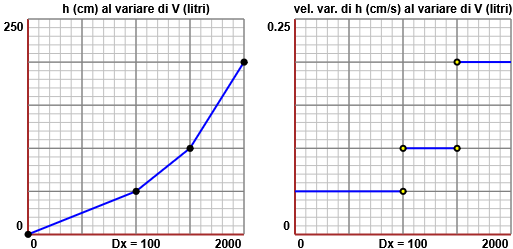 La velocità con cui h varia al variare di V nel primo tratto è 50/1000 = 0.05 cm/litro, ossia mezzo millimetro per litro. Poi, al dimezzarsi della sezione, la velocità raddoppia e diventa 0.1 cm/litro, ossia 1 mm/litro. Infine nell'ultima parte di cisterna diventa di 2 mm/litro. Il grafico sopra a destra illustra come cambia la velocità con cui varia h.
Gli script con cui sono stati realizzati i due grafici li trovi qui e
qui.
La velocità con cui h varia al variare di V nel primo tratto è 50/1000 = 0.05 cm/litro, ossia mezzo millimetro per litro. Poi, al dimezzarsi della sezione, la velocità raddoppia e diventa 0.1 cm/litro, ossia 1 mm/litro. Infine nell'ultima parte di cisterna diventa di 2 mm/litro. Il grafico sopra a destra illustra come cambia la velocità con cui varia h.
Gli script con cui sono stati realizzati i due grafici li trovi qui e
qui.
 Nell'ultimo caso è stato facile studiare esattamente come cambiava la velocità di variazione. Vediamo una situazione più complessa. Sotto a sinistra è riprodotta la visione dall'altro di tre mezzi di trasporto a partire da un certo istante in cui sono affiancati. Il "filmato" è costituito da immagini separate di 1 secondo l'una dalla successiva.
Nell'ultimo caso è stato facile studiare esattamente come cambiava la velocità di variazione. Vediamo una situazione più complessa. Sotto a sinistra è riprodotta la visione dall'altro di tre mezzi di trasporto a partire da un certo istante in cui sono affiancati. Il "filmato" è costituito da immagini separate di 1 secondo l'una dalla successiva.
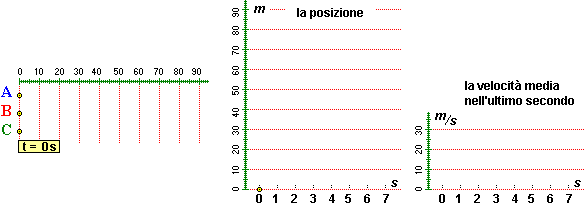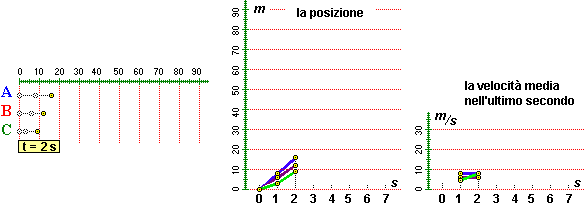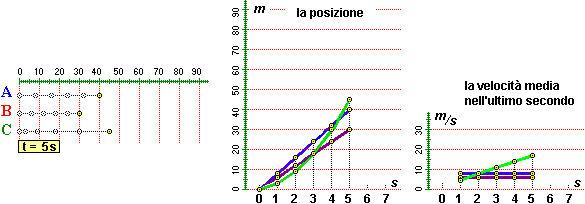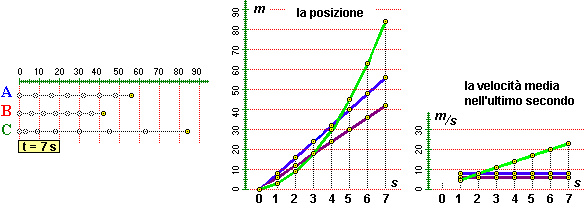 |
| Tre mezzi di trasporto visti dall'alto. | La loro posizione al trascorrere del tempo. | La velocità media nel precedente secondo. |
|
L'auto A in 7 s percorre circa 56 m, con una velocità media di 8 m/s. L'auto C in 7 s percorre circa 84 m, con una velocità media di 12 m/s (84/7 = 12). Ma inizialmente A è più veloce di C, e per più di 4 s rimane davanti a C. Invece B rimane sempre dietro ad A, e la sua distanza da A cresce regolarmente. Il grafico al centro, in cui sono riportate le informazioni (tempo, posizione), ci consente di capire meglio il fenomeno. Quello a destra rappresenta lo spazio percorso nell'ultimo secondo, ossia la velocità media tenuta nel secondo immediatamente precedente: corrisponde alla parte detra della tabella a fianco.
|
tempo
(s) | posizione (m) | variazione della
posizione in 1 s |
| A | B | C | A | B | C |
| 0 | 0 | 0 | 0 | - | - | - |
| 1 | 8 | 6 | 3 | 8 | 6 | 3 |
| 2 | 16 | 12 | 9 | 8 | 6 | 6 |
| 3 | 24 | 18 | 18 | 8 | 6 | 9 |
| 4 | 32 | 24 | 30 | 8 | 6 | 12 |
| 5 | 40 | 30 | 45 | 8 | 6 | 15 |
| 6 | 48 | 36 | 63 | 8 | 6 | 18 |
| 7 | 56 | 42 | 84 | 8 | 6 | 21 |
|
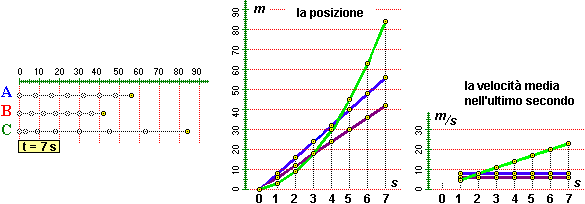
Sopra la situazione è riprodotta fermata al 7° secondo. A e B viaggiano a velocità costante : in 1 sec A percorre 8 m, B ne percorre 6. I grafici delle velocità in m/s.sono quindi delle rette, una con ordinata "8 m", l'altra con ordinata "6 m".
C, invece, sta accelerando. Più precisamente ha velocità che aumenta proporzionalmente al tempo trascorso: ad ogni secondo aumenta di 3 m lo spazio che percorre in 1 secondo, per cui la velocità media che ha in un certo secondo supera di 3 m/s quella che aveva nel secondo precedente.
Si dice anche che C si muove con accelerazione costante. Invece di dire che ad ogni secondo la sua velocità aumenta di 3 m/s si dice che ha una accelerazione di 3 m/s2.
Non siamo tuttavia in grado di descrivere esattamente qual è la velocità che ha C in un dato istante t : nei casi in cui la velocità è costante essa può essere determinata direttamente calcolando una velocità media, negli altri casi, come in quello di C, no. Tuttavia, se rilevassimo la posizione di C invece che ogni secondo in intervalli di tempo più piccoli, otterremmo velocità medie che ci consentono di approssimare meglio i valori esatti della velocità. Ecco la tabella che avremmo ottenuto se avessimo rilevato la posizione di C ogni mezzo secondo:
| tempo (s) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 |
| posizione (m) | 0 | 1.125 | 3 | 5.625 | 9 | 13.125 | 18 | 23.625 | 30 | 37.125 | 45 | 53.625 | 63 | 73.125 | 84 |
| v. media (m/s) | - | 2.25 | 3.75 | 5.25 | 6.75 | 8.25 | 9.75 | 11.25 | 12.75 | 14.25 | 15.75 | 17.25 | 18.75 | 20.25 | 21.75 |
Anche calcolando la velocità media su questi intervalli più piccoli si vede che essa, di secondo in secondo, aumenta di 3 m/s. Ma i valori trovati sono leggeremente più alti di quelli trovati prima (a "tempo = 1 s" ora corrisponde "v.media = 3.75 m/s" invece che "3 m/s): infatti in ogni istante abbiamo fatto il calcolo su un intervallo di tempo più recente. Se restringessimo man mano gli intervallini su cui calcoliamo la velocità media otterremmo via via approssimazioni migliori della velocità.
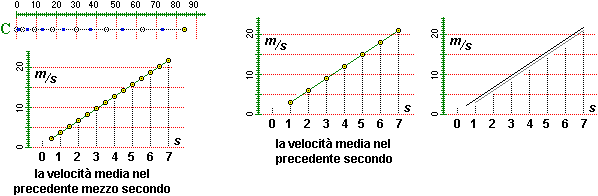
Rilevando la posizione più frequentemente e calcolando la media su questi intervallini
più piccoli si ottengono valori diversi, man mano più vicini ai valori esatti delle velocità.
Potremmo trovare che il grafico della velocità media tende a stabilizzarsi sulla retta di pendenza 3 che per tempo = 0 (s) ha velocità = 1.5 (m/s)descrivibile con la formula (indicando con t il tempo in secondi e con v la velocità in metri al secondo):
v = 3 t + 1.5.
Il mezzo C nell'istante iniziale aveva la velocità di 1.5 m/s e ha proseguito con una accelerazione di 3 m/s2. | 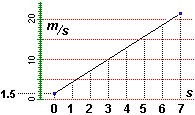 |
 Consideriamo un fenomeno di natura economica. Vivo in un paese in cui la moneta è il Din e devo acquistare un'automobile che costa 2100 Din. Io dispongo di una tale cifra. Il rivenditore d'auto mi fa questa offerta:
Consideriamo un fenomeno di natura economica. Vivo in un paese in cui la moneta è il Din e devo acquistare un'automobile che costa 2100 Din. Io dispongo di una tale cifra. Il rivenditore d'auto mi fa questa offerta:
mi paghi in 7 rate annuali da 300 Din; ciascuna però aumentata con un tasso annuo del 5%, e dell'eventuale tasso di inflazione.
[Se vuoi rivedere le variazioni percentuali:  variazione]
variazione]
Proviamo a descrivere con delle formule a quanti Din ammonta la rata R(t) dopo t anni, supponendo che non ci sia inflazione:
• R(0) = 300 (rata iniziale);
• R(t+1) = R(t) + 5% R(t) = R(t) · (1 + 5/100) = R(t) · 1.05 (la rata dopo 1 anno aumenta del 5%).
Al 2° anno la rata rispetto all'inizio ha subito due aumenti del 5%, ossia è stata moltiplicata 2 volte per (1 + 5/100) = 1.05; in altre parole è stata moltiplicata per 1.052.
Al 3° anno la rata rispetto all'inizio ha subito tre aumenti del 5%, ossia è stata moltiplicata per 1.053.
Al t° anno la rata rispetto all'inizio ha subito t aumenti del 5%, ossia è stata moltiplicata per 1.05t.
In definitiva: R(t) = 300 · 1.05 t.
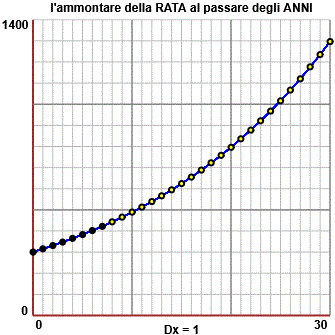
A destra è raffigurato il grafico di R in funzione di t. Per evidenziare meglio l'andamento abbiamo considerato anche valori di t maggiori di 7.
Il fatto che il grafico non sia una retta, ma che la sua pendenza man mano cresca, corrisponde al fatto che le rate di anno in anno non aumentano dello stesso valore (il primo anno aumenta del 5% di 300, ossia di 15, il secondo anno del 5% di 315, ossia di 15.75, …).
[In questo caso non ha senso andare a considerare variazioni in intervalli più piccoli dell'anno in quanto le rate devo pagarle di anno in anno]
Qual è la velocità con cui varia R rispetto a t?.
Ovvero qual è la variazione di R in 1 anno?
| vel. di variaz. = | variaz. di R | = | 5% di R(t) | = 0.05·R(t) |
| ————— | ————— |
| variaz. di t | 1 |
|  |
Siamo di fronte a una situazione in cui la velocità di variazione cresce proprorzionalmente non al tempo (come nel caso del moto con accelerazione costante considerato sopra) ma alla grandezza stessa di cui si studia la variazione.
Un andamento di questo tipo si dice esponenziale in quanto si tratta di grandezze descrivibili con formule del tipo di R(t) = 200 · 1.05 t, cioè mediante un elevamento alla potenza (con la variabile di input ad esponente). Lo script con cui è stato realizzato il grafico lo trovi qui.
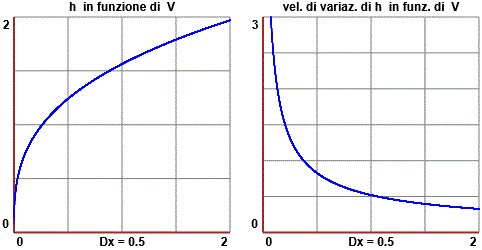
 Nel caso seguente, invece, siamo di fronte a una grandezza (il livello h di un recipiente di forma conica in funzione del volume V di liquido introdotto) che ha velocità di variazione che man mano decresce: infatti via via che il liquido sale la superficie si allarga per cui il nuovo liquido che entra si distribuisce su un'area maggiore e, quindi, dà luogo ad un innalzamento minore.
Nel caso seguente, invece, siamo di fronte a una grandezza (il livello h di un recipiente di forma conica in funzione del volume V di liquido introdotto) che ha velocità di variazione che man mano decresce: infatti via via che il liquido sale la superficie si allarga per cui il nuovo liquido che entra si distribuisce su un'area maggiore e, quindi, dà luogo ad un innalzamento minore.
Lasciamo come esercizio dimostrare che h in funzione di V nel caso in cui il cono abbia altezza 2 e raggio 1 è espresso da h = (12 V/π)1/3 e capire perché il suo grafico abbia effettivamente l'andamento raffigurato sotto al centro. A destra è tracciato il grafico della velocità di variazione di h rispetto ad V, che visualizza il rallentamento progressivo della crescita del livello. Gli script con cui sono stati realizzati i due grafici li trovi qui
e qui.
 Nell'ultimo caso non è facile dalla formula che esprime come varia la grandezza (h in funzione di V) dedurre l'espressione e il grafico esatto della velocità di variazione. In una voce successiva vedremo come il concetto di derivata ci renderà semplici deduzioni come questa e ci consentirà di descrivere in modo sintetico e di studiare situazioni di vario genere in cui si conosce la velocità o l'accelerazione con cui varia una certa grandezza (di tipo fisico od economico o …). Alle voci
Nell'ultimo caso non è facile dalla formula che esprime come varia la grandezza (h in funzione di V) dedurre l'espressione e il grafico esatto della velocità di variazione. In una voce successiva vedremo come il concetto di derivata ci renderà semplici deduzioni come questa e ci consentirà di descrivere in modo sintetico e di studiare situazioni di vario genere in cui si conosce la velocità o l'accelerazione con cui varia una certa grandezza (di tipo fisico od economico o …). Alle voci  pendenza 2 e
pendenza 2 e  rette tangenti e curve vengono proposte altre idee e tecniche che possono introdurre al concetto di derivata.
rette tangenti e curve vengono proposte altre idee e tecniche che possono introdurre al concetto di derivata.
Esercizio e soluzione.
 Il grafico che segue rappresenta una funzione interessante: la temperatura al variare del tempo rilevata alla stazione meteo di Sassello (paese ad 800 m di altitudine, in provincia di Savona), nei primi 8 giorni del febbraio del 2012. Abbiamo riportato solo i valori registrati ogni 3 ore. [qui lo script in cui puoi recuperare i dati]
Il grafico che segue rappresenta una funzione interessante: la temperatura al variare del tempo rilevata alla stazione meteo di Sassello (paese ad 800 m di altitudine, in provincia di Savona), nei primi 8 giorni del febbraio del 2012. Abbiamo riportato solo i valori registrati ogni 3 ore. [qui lo script in cui puoi recuperare i dati]











