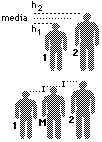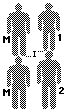Valori medi (1)

  Si chiama media di più numeri il rapporto tra la loro somma e la loro quantità:

         numero1 + numero2 + ... + numeroN
media = ———————————————————————————————————
                         N

Il consumo pro-capite è la media aritmetica dei consumi effettuati da tutti gli abitanti: in questo caso numero 1, numero 2, .... , numero N sono i consumi (in lire, chilogrammi, …, a seconda dei casi) di ciascuno degli N abitanti del paese considerato. Il valore che si ottiene indica, in pratica, quanto consumerebbe ogni abitante se il consumo complessivo della popolazione fosse ripartito in parti uguali.

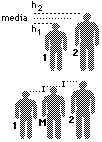Dati uomo-1 e uomo-2 alti, rispettivamente, h1 cm e h2 cm, la loro altezza media (in cm) è la media aritmetica di h1 e h2. In questo caso la media rappresenta l'altezza che sta a metà tra h1 e h2. Infatti se consideriamo un uomo-M con altezza a metà tra h1 e h2 (ottenibile da uomo-1 allungandolo di metà del dislivello tra h1 e h2 o da uomo-2 accorciandolo della stessa quantità) e ne sovrapponiamo due copie, raggiungiamo la stessa l'altezza h1+h2 che si ottiene sovrapponendo uomo-1 e uomo-2. Quindi l'altezza di uomo-M è proprio pari a (h1+h2)/2.

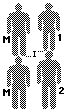  Consumo medio e altezza media sono valori medi nel senso che, con un unico numero, ci forniscono un'idea del livello di consumo o delle altezze di una popolazione. Tuttavia non tengono conto delle differenze tra individuo e individuo, che a volte possono essere notevoli: dietro a un consumo procapite di 70 g di carne al giorno vi può essere chi non ne mangia quasi mai e chi ne consuma giornalmente qualche etto.

  Anche la velocità media con cui un mezzo di trasporto ha percorso un certo itinerario è un valore medio: ci dà un'idea di come ha viaggiato il mezzo di trasporto senza una descrizione dettagliata di come la velocità è variata nei diversi tratti di strada:  è la velocità costante a cui si dovrebbe viaggiare in ciascun tratto per impiegare lo stesso tempo complessivo.  Tuttavia non si ottiene facendo la media aritmetica di più velocità ma come rapporto tra strada percorsa e tempo impiegato:

velocità media =	strada percorsa
	————————
	tempo impiegato

Si noti che abbiamo parlato di "strada percorsa" e non di "spostamento", in quanto con quest'ultimo termine si intende la strada che si sarebbe percorsa per andare dal punto di partenza a quello di arrivo se si fosse proceduto in modo rettilineo. Ad esempio se il punto di arrivo coincidesse con quello di partenza, lo spostamento, qualunque percorso si seguisse, sarebbe nullo.

Esempio. Un'auto viaggia per 1 ora e mezza alla velocità media di 80 km/h e nell'ora successiva alla velocità media di 60 km/h. Qual è la velocità media dell'auto nel complesso del viaggio? Non è 70 km/h, anche se 70 è la media di 60 e 80. Nel primo tratto percorre 1.5·80 = 120 km; nel secondo 60 km. Nelle 2 ore e mezza di viaggio percorre quindi 180 km. La velocità media è 180/2.5 = 90·2·4/10 = 9·8· = 72 km/h. 72 è più vicino a 80 che a 60 in quanto è maggiore il tempo che ha viaggiato a 80 km/h.

Nota.  Dati i numeri A, B e C, viene chiamata media armonica di A, B e C il numero 3/(1/A+1/B+1/C), ossia il reciproco della media aritmetica dei reciproci di A, B e C. La definizione viene generalizzata in modo ovvio al caso in cui i numeri siano N invece che 3.  Se un'auto dalla località X alla località Y viaggia mediamente a 50 km/h e, poi, da Y ad X a 60 km/h, complessivamente, indicata con D la distanza in chilometri tra X ed Y, ha impiegato D/50+D/60 ore e ha tenuto la velocità media 2·D/(D/50+D/60) = 2/(1/50+1/60) km/h = 54.54… km/h, ossia la media armonica delle due velocità.

  Analoghi al concetto di velocità media sono i concetti di pendenza media e di variazione media. Ad esempio per dire che nel periodo 1960 - 63 il grafico dei record di salto in alto (sotto a sinistra) è più ripido che nel 1963 - 78 possiamo dire che la sua pendenza media (rapporto tra avanzamento verticale e avanzamento orizzontale) nel primo intervallo è maggiore.
   Senza andare a misurare con il righello i due avanzamenti possiamo esprimere numericamente la pendenza mediante l'aumento medio annuo, cioè il rapporto tra aumento del record (variazione dei valori rappresentati sull'asse verticale) e numero degli anni trascorsi (variazione dei valori rappresentati sull'asse orizzontale).

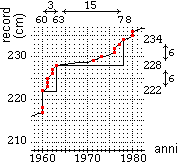Esprimendosi in "cm all'anno": 1960-63: 228 - 222 6 aumento medio = ——————————— = ——— = 2 63 - 60 3 1963-78: 234 - 228 6 aumento medio = ——————————— = —— = 0.4 78 - 63 15

  Se dispongo dei valori medi riferiti alle parti che compongono una popolazione, per trovare il valore medio riferito all'intera popolazione non posso fare la media aritmetica di questi dati: i dati medi relativi alle parti più numerose devono "pesare" maggiormente, facendo avvicinare a sé il valore relativo all'intera popolazione.

È la stessa osservazione che abbiamo fatto alla fine del precedente esempio sul calcolo della velocità media. La situazione è analoga a quella raffigurata a fianco: il punto di equilibrio deve esser più vicino all'oggetto che pesa di più.

Ad esempio se in una famiglia i 4 adulti consumano a testa mediamente 200 ml di latte al giorno mentre i 2 bambini ne consumano mediamente 500 ml a testa, il consumo medio giornaliero di latte di un membro della famiglia Bianchi non si ottiene facendo (200+500)/2=350 ml, ma devo tener conto che 200 ml è la media tra 4 persone, per cui corrisponde a un consumo complessivo di 200·4 ml, e che 500 ml è la media tra 2 persone, per cui corrisponde a un consumo complessivo di 500·2 ml. In definitiva:

 
                    somma dei consumi individuali
consumo procapite = ————————————————————————————— = 
                        numero degli individui

 
  200·4+500·2   1800
= ——————————— = ————  = 300 (ml di latte)
     4+2          6 

Si affronta in maniera analoga anche un problema di questo genere:

«se mescolo 0.40 l di succo di arancia, 0.20 l di liquore a 40° e 0.30 l di liquore a 18°, qual è la gradazione del cocktail ottenuto?». (ricorda che "vino di 12° (12 gradi)" sta per "vino con 12% di alcol")

GradazioneCocktail =


     AlcolTotale     AlcolSucco + AlcolA + AlcolB
 = —————————————— = ————————————————————————————— =
    LiquidoTotale          0.40+0.20+0.30

 
  0.40·0%+0.20·40%+0.30·18%   0+0.08+0.054
= ————————————————————————— = ———————————— = 0.149 = 14.9%
        0.90                      0.90

  Alcune calcolatrici sono in grado di calcolare automaticamente le medie aritmetiche.  Con la "calcolatrice pccola" a cui puoi accedere da  QUI  basta che copi sul "visore" (171+183+190+176)/4 per ottenere la media aritmetica di 171, 183, 190 e 176, o  (234-228)/(78-63)  e  (0.2*0.4+0.3*0.18)/(0.4+0.2+0.3)  per ottenere i risultati di alcuni dei calcoli considerati sopra.