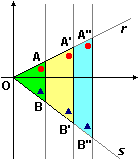
La figura precedente illustra una proprietà famosa: il teorema delle proiezioni parallele (che in Italia, a scuola, viene spesso chiamato anche teorema di Talete, anche se non è da attribuire a questo matematico e filosofo greco del VI secolo a.C.):  fissate due rette r e s e una inclinazione α diversa da quelle di r e s, la proiezione di r su s di inclinazione α trasforma i segmenti proporzionalmente.
    Nella figura la situazione è stata rappresentata in modo che l'inclinazione α coincida con quella dell'asse y.  La proprietà può essere tradotta così:
un fascio di "raggi" paralleli proietta due qualunque segmenti di r  (AA' e A'A", o OA e A'A", o …)  in modo che le loro immagini  (BB' e B'B", o OB e B'B", o …)  su s hanno tra loro lo stesso rapporto che c'è tra i segmenti originali.
    La dimostrazione è facile:  su ogni retta non verticale  le x, le y e, quindi, anche le distanze, hanno variazioni proporzionali.  In particolare se su r un segmento è doppio di un altro allora gli estremi dell'uno hanno Δx doppio del Δx degli estremi dell'altro e, quindi, anche i corrispondenti segmenti su s sono l'uno il doppio dell'altro.