Rette tangenti e curve - 1

  Il concetto di retta tangente

    Abbiamo già introdotto il concetto di retta tangente nel caso del cerchio: è la retta che "tocca" il cerchio senza attraversarlo.

"Tangente" è un termine usato anche nel linguaggio comune:  si usa dire che una persona, nella foga di una discussione, "parte per la tangente" quando incomincia a divagare, a perdere il filo e il controllo delle argomentazioni, proseguendo lungo la direzione che il discorso ha preso al momento.  Questo modo di dire deriva dal fatto che se faccio ruotare un oggetto attaccato a un filo e ad un certo punto questo si spezza, perdo il controllo dell'oggetto ed esso prosegue lungo la tangente. Questa proprietà era usata dai frombolieri: essi lasciavano partire il proiettile dalla fionda quando questo, liberato, avrebbe proseguito lungo la direzione voluta, ossia quando la retta tangente alla traiettoria del proiettile coincideva con la direzione voluta. Analogamente un treno che deragli in un tratto in cui i binari hanno andamento circolare tende a proseguire in modo rettilineo lungo la tangente all'arco di cerchio.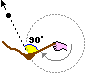

    È anche facile tracciare la tangente in un punto P ad un cerchio, se ne conosciamo il centro: basta tracciare il raggio che passa per P e la retta per P perpendicolare a tale raggio.
    Come si può descrivere e come si può tracciare la tangente in un punto ad un altro tipo di curva?

  Nel caso del cerchio possiamo descrivere la tangente in un punto come la retta che ha solo quel punto in comune con esso. Questa descrizione va bene anche per l'ellisse: vedi figura (1) sottostante. Ma se prendessimo come curva solo solo il pezzo dell'ellisse selezionato con il rettangolo punteggiato, sarebbero infinite le rette che passano per il punto evidenziato e non hanno altri punti in comune con tale curva.
    Proviamo a descrivere la tangente a una curva in un punto come la retta che ha solo quel punto in comune con la curva e lascia il resto della curva dalla stessa parte rispetto a sé stessa.
    Questa descrizione va bene anche per il punto A della figura (2). Ma non va bene per il punto B: la retta tracciata per esso è intuitivamente tangente alla curva, ma non la lascia tutta dalla stessa parte; infatti la attraversa in un altro punto.
    Possiamo rimediare alla cosa richiedendo non che tutta la curva stia dalla stessa parte, ma che questo avvenga solo in un intorno del punto, cioè per il pezzo di curva racchiuso in un cerchietto centrato nel punto.
    Questa descrizione soddisfa anche il caso del punto B. Ma che dire della tangente in C?

    Come tangente in C è naturale (tenendo conto di quanto osservato sopra sul "partire per la tangente") prendere la retta tracciata in figura, lungo cui tenderebbe a proseguire un veicolo che, seguendo una traiettoria come quella rappresentata in (2), perdesse improvvisamente il controllo della strada mentre passa per C.  Ma in questo caso la retta tangente taglierebbe la curva, non la lascerebbe tutta dalla stessa parte.
    E nel caso della figura (3)? Per il punto A passano infinite rette che hanno un unico punto in comune con la curva e la lasciano tutta dalla stessa parte. E la tangente in B dovrebbe essere la retta passante per B che contiene la curva (è questa la traiettoria rettilinea lungo cui ci si muove passando per B), ma questa retta ha infiniti punti in comune con la curva.
    Anche la curva (4) ci pone alcuni problemi: se la interpretiamo come una traiettoria, un veicolo raggiunge A con una certa direzione e ne riparte con una diversa. Quale delle due rette dovremmo considerare tangente?
    Abbiamo, dunque, visto che non è facile definire in generale il concetto di retta tangente in modo che rispecchi il significato che intuitivamente gli attribuiamo.

  Oltre al problema di come definire la retta tangente, dobbiamo anche porci il problema di come tracciarla. Ad es. nel caso dell'ellisse non circolare di figura (1) è difficile tracciare una retta passante per A con l'inclinazione giusta: come riconoscere ad occhio in un disegno tra due rette diversamente inclinate che non attraversino clamorosamente la curva quale è effettivamente tangente?
    Nel caso dell'ellisse, invero, si potrebbe trasformarla in un cerchio con una trasformazione di scala, tracciare la tangente nel punto A' del cerchio che corrisponde ad A e applicare la trasformazione di scala inversa: la tangente al cerchio viene trasformata nella tangente all'ellisse. Ma nel caso della figura (2) non si può usare questo trucco.

Precisare il concetto e il modo di tracciare le tangenti ci serve anche per affrontare situazioni come quella illustrata a lato: qual è l'angolo formato da due traiettorie non rettilinee che si intersecano? È naturale prendere l'angolo formato dalle rette tangenti alle due traiettorie nel punto di intersezione.

    Problemi analoghi dobbiamo porci se vogliamo capire come fa una applicazione grafica per computer a realizzare le tangenti a una curva? o, viceversa, a tracciare, data una certa retta e un certo punto, una curva che in quel punto abbia tale retta come tangente?
    Consideriamo ad es. il tracciamento di tratti curvilinei usando in Paint o usando "bottoni", menu o comandi simili in altri tipi di applicazioni:
(1) si individuano, cliccando, due punti P e Q; appare un segmento che li ha come vertici; (2) si clicca su un punto P₁; il segmento si incurva nella direzione di esso; (3) se poi clicco su un altro punto P₂ la curva si deforma ulteriormente, in modo tale da assumere un andamento che richiama la forma della spezzata P P₁P₂Q 

(1)

(2)

(3)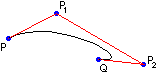

Osservando le figure si intuisce che la curva si dispone prima in modo che i segmenti PP1 e QP1 siano tangenti alla curva in P e Q, poi in modo che lo siano i segmenti PP1 e QP2. Questa osservazione è confermata se si clicca sul punto P2 nel modo illustrato a lato: la curva viene tirata verso P1 e verso P2 in modo che PP1 sia tangente in P e QP2 lo sia in Q.

(3')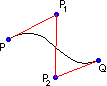

    Come fa questo programma a comportarsi in questo modo? Che cosa vuol dire per esso che una retta sia tangente a una curva?  [curve di questo tipo sono chiamate curve di Bezier, dal nome di colui che le ha ideate].

  Il concetto di curva

    Prima di affrontare questi aspetti dobbiamo porci un ulteriore problema. Che cosa è una curva?

Innanzi tutto osserviamo che nel linguaggio comune mentre della linea A sopra tracciata si dice che è una curva oppure un profilo, una traiettoria, … curvilinea, la stessa cosa non viene detta di B, che ha andamento rettilineo, né di C o di D, che presentano dei punti angolosi, ossia dei punti in cui, percorrendo la linea da un capo all'altro, si arriva con una direzione e se ne riparte con un'altra (in casi come quello a destra, in cui le direzioni sono opposte, ossia formano un angolo di ampiezza 0, il punto angoloso è chiamato cuspide).  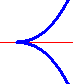   In matematica, invece, tutte e quattro le linee vengono chiamate curve; si dice eventualmente che A è una curva non rettilinea.  Questo uso più generale della terminologia che si fa in matematica è presente in moltissime altre situazioni:

• nell'usuale comunicazione - anche quando si parla di matematica - dicendo «ho un tavolo rettangolare», «non arrivo a 38° di febbre», «disegna un'ellisse» … voglio dire anche che il tavolo non è quadrato, informare che la mia temperatura corporea supera i 37°, chiedere di non disegnare un cerchio, … in quanto altrimenti avrei specificato diversamente la forma del tavolo, la mia temperatura, la figura da disegnare, …;
• nell'enunciare una proprietà o una definizione matematica, invece, se parlo di un rettangolo o di una ellisse o ad esempio di un trapezio non escludo che sia, rispettivamente, un quadrato o un cerchio o un rettangolo, se scrivo "x < 38" includo la possibilità che x sia "molto" più piccolo di 38, ….

    Questo uso di definizioni più estese rispetto al linguaggio comune è indispensabile per poter descrivere procedimenti, svolgere argomentazioni, … in modo generale.  Per fare un esempio chiarificatore, si pensi alla descrizione del metodo dei trapezi per determinare l'area di un poligono a partire dalle coordinate dei suoi vertici:  il poligono viene interpretato come somme e differenze di trapezi con "basi" verticali, e se si escludessero dai trapezi i rettangoli (come si fa nel linguaggio comune) la descrizione non funzionerebbe nel caso in cui il poligono abbia dei lati orizzontali..