Rapporto

  Il rapporto è un concetto impiegato per esprimere la relazione che intercorre tra le misure di due grandezze. Nel caso di grandezze dello stesso tipo, esso non è altro che il risultato della divisione tra il numero che esprime la prima misura e il numero che esprime la seconda (a patto che esse siano espresse nella stessa unità di misura). È una generalizzazione del concetto di divisione per "contenenza" (la divisione del tipo (B) descritta alla voce  Le "quattro operazioni").

Per esprimere il concetto di rapporto si ricorre al simbolo di divisione, sia nella forma ":" che nelle forme "/" e "", e a varie descrizioni verbali.

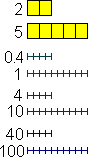	e può essere letto, oltre che come «2 diviso 5», anche come «2 a 5» o come frazione: «2 quinti» (2 cm sono 2 volte la quinta parte di 5 cm); la lettura sotto forma di frazione si usa solo se i due numeri sono interi.
	Calcolando il risultato della divisione (2 diviso 5 fa 0.4) si può dire che il rapporto tra 2 cm e 5 cm è 0.4. In altre parole 2 cm è pari a 0.4 volte 5 cm.
	Anche il rapporto tra 0.4 e 1, tra 4 e 10, tra 40 e 100, … è uguale a 0.4: le divisioni 2/5, 0.4/1, 4/10, 40/100, … fanno tutte 0.4. Si usa dire anche che 2 sta a 5 come 0.4 sta a 1 o come 4 sta a 10 o come 4 sta a 100 o …
"H è 4 volte K", "H = 4K", "H = K·4" sono tutti modi per esprimere il fatto che il rapporto tra H e K è 4.   "H è 2 1/4 volte K" (H è 2 volte e 1/4 K) è un modo spesso usato per esprimere il fatto che il rapporto tra H e K è 2+1/4, ovvero 2.25, cioè il fatto che H=K·(2+1/4); occorre stare attenti a non confondere 2 1/4 con 2·1/4.   "H è 3/4 di K" si può esprimere anche come "H è 3/4 volte K" (pur se suona male), come H = K·(3/4) o H = 3/4 K.
Nota. La parola frazione è presa a prestito dal linguaggio comune ma con un significato diverso: nel linguaggio comune indica, in genere, una porzione, una parte staccata da qualcosa, e non è detto che si tratti di una quantità il cui rapporto col "tutto" sia esprimibile come rapporto tra due interi. In matematica, invece, si considerano come frazioni solo rapporti tra interi, e questi possono essere anche maggiori di 1, ossia esprimere quantità maggiori della quantità con cui si fa il confronto. È sbagliato usare il significato "matematico" in contesti in cui viene usualmente usato in altro modo (ad es. non avrebbe senso in una conversazione dire che la popolazione europea è una frazione della popolazione italiana, anche se è vero che il rapporto tra popolazione europea e popolazione italiana è un rapporto tra interi).   A volte si parla di termini frazionari anche di fronte a generici rapporti, ossia ad espressioni del tipo  termine / termine.  In questi casi, come di fronte al rapporto tra interi 3/4 il "4" viene detto denominatore, in quanto dà il nome alle parti (i "quarti") che si devono prendere, e il "3" viene detto numeratore, in quanto esprime il numero delle volte che le parti devono essere prese, così il primo e il secondo termine del rapporto vengono spesso chiamati, rispettivamente, "termine a numeratore" e "termine a denominatore".   Ricordiamo, infine, che a volte si parla di frazione propria per indicare un rapporto tra due numeri positivi che sia minore di uno, ossia in cui il primo sia minore del secondo.

  Per facilitare i confronti spesso si usa rappresentare i rapporti in forma percentuale . Ad esempio nel caso precedente (rapporto tra 2 cm e 5 cm) o nel caso del rapporto tra le 200 mila lire del prezzo in saldo di un prodotto e il prezzo originale di 500 mila lire o nel caso dei 20 milioni di abitanti della regione A in confronto con i 50 milioni della regione B, … possiamo dire sia che il rapporto è 0.4, sia che il rapporto è 40 centesimi o, più in breve, 40 per cento (in simboli: 40%):

2 cm sono il 40% di 5 cm, 200 mila lire sono il 40% di 500 mila lire (sono 500 mila lire scontate del 60%: da 100 centesimi sono passato a 40 centesimi: 60 centesimi in meno), la popolazione di A è pari al 40% della popolazione di B, …

Osserviamo che % (barra e due "0") è semplicemente un'abbreviazione di  "/100":  5% sta per 5/100.  Analogamente la scrittura ‰ è un'abbreviazione di  "/1000":  5‰ (5 per mille) sta per 5/1000.

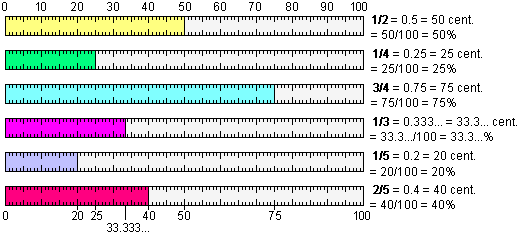
Questa rappresentazione è particolarmente efficace in quanto è facile immaginare una striscia lunga 100 mm e confrontarla visivamente con una sua parte lunga 40 mm, e sappiamo, per esperienza, associare i rapporti del tipo "1 a …" di uso più comune alle loro rappresentazioni percentuali:

  Nell'esempio precedente il numero 40, che esprime il rapporto come quantità di centesimi, viene chiamato parte percentuale o percentuale. Non è altro che il rapporto moltiplicato per 100. Più in generale dati due valori A e B, la percentuale che esprime il rapporto tra A e B è calcolabile così:

A percentuale = ———·100 B

I rapporti sono spesso rappresentati anche in millesimi, sessantesimi, trentesimi, 360-esimi,… . La trasformazione è analoga a quella usata per le parti percentuali:

A ParteMillesimale = ———·1000 ,  B

A ParteSessagesimale = ———·60 ,  B

...

Pur essendo più piccolo di 100, 60 è divisibile esattamente (cioè con risultato intero) in più modi, e quindi consente di esprimere più facilmente molti rapporti d'uso comune: 1/3 d'ora diventa 20 minuti; se dividessimo l'ora in 100 minuti dovremmo parlare di 33.333… minuti. La figura sottostante illustra i rapporti del tipo 1/n, con n numero naturale, rappresentabili esattamente in sessantesimi, cioè con una quantità intera di divisioni (in un cerchio ripartito in 60 divisioni):

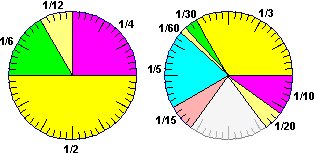oltre a 1 (sessanta divisioni),  1/2 (30 divisioni),  1/3 (20 divisioni),  1/4 (15 divisioni),  1/5 (20 divisioni),  1/6 (10 divisioni),  1/10 (6 divisioni),  1/12 (5 divisioni),  1/15 (4 divisioni),  1/20 (3 divisioni),  1/30 (2 divisioni),  1/60 (1 divisione).

  Le percentuali facilitano il confronto tra le parti che compongono un totale, tra una parte e il totale, … , ma, in cambio, perdono altre informazioni. Ad esempio l'incidenza della carne bovina sul totale della carne consumata pro-capite dal 1926 al 1985 passa dal 47% al 32%, ma ciò non significa che diminuisce il consumo di carne bovina: se si analizzano i dati assoluti (cioè non rapportati al totale del consumo di carne) si osserva che si passa dal consumo pro-capite di 10.1 kg all'anno a quello di 25.1 kg all'anno: se un certo dato aumenta ma, nel frattempo, aumenta anche il totale, la percentuale che lo rappresenta può diminuire.

  Nel caso di grandezze di tipo diverso, indicando il rapporto tra le loro misure occorre anche specificare le unità di misura impiegate. Ad esempio il rapporto tra la popolazione di una regione e l'estensione della stessa può essere espresso in abitanti/km² o in abitanti/m²("abitanti per km²", "abitanti per m²"), quello tra strada percorsa e tempo impiegato può essere espresso in km/h o m/s o … ("chilometri all'ora", "metri al secondo", …).

  La trasformazione di un rapporto tra numeri naturali, ovvero di una frazione, in un rapporto tra interi più piccoli viene chiamata semplificazione.  Ad esempio la frazione 150/100 può essere semplificata in 15/10, che a sua volta può essere semplificata in 3/2.  Possiamo realizzare le semplificazioni con moltissime applicazioni software.  Ad esempio possiamo usare la "piccolissima" calcolatrice presente QUI (o la più semplice "calcoli"):

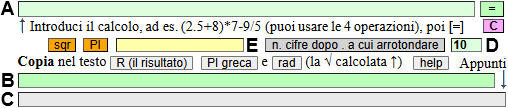
Se metto in A 100/375 ottengo il valore numerico 0.2666666667 e la semplificazione 4/15.  Se metto 140/105 ottengo 4/3.  Se metto 1275/3000 ottengo 17/40.

    Vi sono alcuni semplici metodi per semplificare "a mano" una frazione, che si basano sulla individuazione di numeri per cui entrambi gli elementi della frazione siano divisibili:  se i due elementi terminano per 0 (o 00) posso entrambi dividerli per 10 (o per 100), se terminano con una cifra pari sono entrambi divisibili per 2, se terminano entrambi per 0 o per 5 sono entrambi divisibili per 5 (ma conviene moltiplicarli entrambi per 2 in modo da avere numeri terminanti per 0), se la somma delle cifre dei due numeri è divisibile per 3 (o per 9) sono entrambi divisibili per 3 (o per 9).  Alcuni esempi:
4500/3500 [tolgo 00] → 45/35 [moltiplico per 2] → 90/70 [tolgo 0] → 9/7
735/120 [moltiplico per 2] → 1470/240 [divido per 10] → 147/24 [1+4+7 = 12, 1+2 = 3; 2+4= 6, sono entramni divisibile per 3] → 49/8
594/81 [5+4+9=9+9 divisible per 9, 8+1=9, sono entrambi divisibili per 9] → 66/9 [sono evidentemente divisibili per 3] → 22/3
 

Esercizi:   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione

Altri esercizi per la scuola di base