Il nostro apparato visivo (occhio+cervello), grazie a forme di elaborazione in parte congenite e in parte sviluppate attraverso l'esperienza, è in grado di interpretare come immagine 3D (a 3 dimensioni) l'immagine 2D (a 2 dimensioni) che arriva sulla retina. Potremmo dire che abbiamo "incoporato" qualche procedimento matematico che ci consente ciò. Questo nostro "vedere non solo con gli occhi" è anche uno dei fattori di un particolare tipo di illusioni ottiche, chiamate paradossi della visione.
Si consideri ad es. la figura a fianco. È costituita dall'unione di tre parallelogrammi, ma alla nostra vista sembra che il lato più alto del parallelogramma più grande sia più lungo del lato opposto. Ciò accade in quanto il nostro occhio interpreta la figura come l'immagine 2D di un oggetto 3D e quindi tende a percepire il lato "lontano" come più lungo, per compensare l'effetto prospettico, sopra discusso, della riduzione degli oggetti più lontani.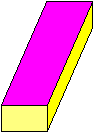

A destra è illustrato un altro fenomeno: un ambiente è deformato in modo da produrre la stessa immagine di una camera normale; l'uomo che appare piccolo in realtà è alto come l'altro uomo, ma è piazzato più lontano. La forma della stanza (chiamata "camera di Ames"), e la collocazione del punto di vista, sono stali da dare l'impressione che si tratti di ambiente a forma di parallelepideo rettangolo. Nel disegno A' rappresenta l'interperatazione della collocazione che dà l'osservazione dell'uomo a sinistra, che in realtà è posto in A.

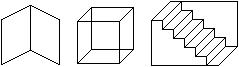Nel caso delle figure soprastanti tendiamo a parcepirle come rappresentazioni di oggetti tridimensionali a noi noti (un libro aperto, un cubo, delle scale), ma la loro errata prospettiva (lati vicini e lontani sono rappresentati nelle stesse dimensioni) ci crea ambiguità interpretativa, se non un vero e proprio distrurbo fisico: se fissiamo gli oggetti dopo un po' ci appaiono diversi, e poi la nostra impressione cambia ancora. Non riusciamo a fissare quali componenti sono da intendere in primo piano e quali in secondo. Solo aggiungendo dei colori o dei particolari, come sotto, riusciamo a sciogliere l'ambiguità.

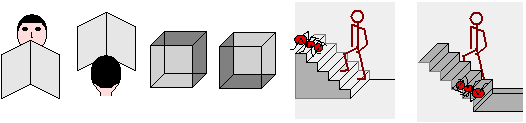   Anche la figura a destra rappresenta una scala, ma qui l'ambiguità è diversa: non è tra vicino e lontano come accadeva per la scala di sopra (che, a seconda di che cosa si interpretava come "muro", portava a intendere la scala come vista dall'alto o dal basso), ma è legata al fatto che vengono unite due figure che corrispondono a punti di vista diversi: è la vista globale della figura che ci disturba; se ne copriamo la parte superiore o inferiore il conflitto sparisce.

Qualcosa di simile accade per la figura sopra a sinistra: se mettiamo a fuoco la parte destra della figura vediamo un coniglio; se mettiamo a fuoco quella sinistra vediamo un'anatra.

   Anche la figura a destra (nota come "triangolo impossibile") ci crea un distrurbo visivo solo se la guardiamo globalmente, in tutti i suoi vertici: è l'unione di 3 figure fatte a "7", ma ci richiama l'idea della rappresentazione piana di un solido che non riusciamo a interpretare.
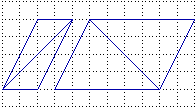
La figura a sinistra mette in luce altri limiti della nostra intuizione spaziale: due segmenti uguali, formati ciascuno da 4 diagonali di quadretto, a prima vista ci sembrano diversi.

Questo fenomeno in parte può essere interpretato, come si è fatto per la prima figura, in relazione a un tentativo di interpretazione 3D, in parte in relazione ad altri problemi percettivi, legati alla contemporanea presenza di parti di figura disposte diversamente o colorate diversamente, che ci fanno apparire segmenti uguali come diversi, rette parallele come incidenti, line rette come incurvate, rettangoli come figure non rettangolari, esemplificabili con le immagini seguenti (nell'ultima vediamo dei pallini grigi che in realtà non esistono).

Di questi aspetti non ci occupiamo.
Più avanti ci occuperemo invece di alcuni problemi più specifici, come quello illustrato dalla figura a lato.
Guardo una figura tracciata sul terreno da una distanza di circa 20 m e da un'altezza iniziale di 2 m. Vicino alla figura è collocato un sistema di "assi" di riferimento, con assi finiti (lunghi 10 m ciascuno). La figura sembra un arco di ellisse. Ma man mano che mi alzo (l'altezza passa da 2 m a 60 m) la figura mi appare come una parabola.
È possibile che una parabola venga vista come un'ellisse?


	Anche la figura a destra rappresenta una scala, ma qui l'ambiguità è diversa: non è tra vicino e lontano come accadeva per la scala di sopra (che, a seconda di che cosa si interpretava come "muro", portava a intendere la scala come vista dall'alto o dal basso), ma è legata al fatto che vengono unite due figure che corrispondono a punti di vista diversi: è la vista globale della figura che ci disturba; se ne copriamo la parte superiore o inferiore il conflitto sparisce.
Qualcosa di simile accade per la figura sopra a sinistra: se mettiamo a fuoco la parte destra della figura vediamo un coniglio; se mettiamo a fuoco quella sinistra vediamo un'anatra.
	Anche la figura a destra (nota come "triangolo impossibile") ci crea un distrurbo visivo solo se la guardiamo globalmente, in tutti i suoi vertici: è l'unione di 3 figure fatte a "7", ma ci richiama l'idea della rappresentazione piana di un solido che non riusciamo a interpretare. La figura a sinistra mette in luce altri limiti della nostra intuizione spaziale: due segmenti uguali, formati ciascuno da 4 diagonali di quadretto, a prima vista ci sembrano diversi.