Modello

  Con la parola modello si intende una rappresentazione di qualche "cosa" (una situazione, un fenomeno, un oggetto, una collezione di oggetti, …) che viene impiegata al posto di questa cosa.

   Gli scopi per cui si impiega un modello possono essere molto vari:
•  migliorare la visualizzazione (per es. usare una riproduzione in scala al posto della figura originale),
•  generalizzare proprietà (per es. dare la regola grammaticale "i nomi maschili terminanti in –o passando al femminile modificano –o in –a" al posto dell'elenco: "abbonato → abbonata, accusato → accusata, …"),
•  permettere confronti (per es. paragonare regioni diverse usando la densità di popolazione invece dei numeri di abitanti e di chilometri quadrati di superficie),
•  cogliere gli aspetti e le cause essenziali di un certo evento (per es. la ricostruzione dei fattori che sono stati all'origine di un certo evento dell'antichità e la sua descrizione che vengono fatte da un manuale di storia),
•  ...

  I modelli possono trascurare o deformare degli aspetti che sono presenti nella cosa originale (le regole grammaticali perdono le "eccezioni", le riproduzioni cartografiche non rappresentano fedelmente le distanze, il dato della densità di popolazione non permette di ritrovare quanto è estesa la regione o quanti sono gli abitanti, l'interpretazione che uno storico dà alle informazioni a disposizione su un certo evento è soggettiva e può differire da quelle di un altro storico, ...). Sono rappresentazioni semplificate che possono facilitare la comunicazione, il ragionamento, …, ma che devono essere interpretate tenendo conto dei loro limiti [ad esempio le percentuali facilitano il confronto tra le parti che compongono un totale e tra una parte e il totale, ma, in cambio, perdono altre informazioni: l'incidenza della carne bovina sul totale della carne consumata pro-capite dal 1926 al 1985 passa dal 47% al 32%, ma il consumo pro-capite passa da 10.1 kg all'anno a quello di 25.1 kg all'anno]

  Per una stessa situazione si possono considerare modelli diversi; in certi casi può risultare più conveniente un modello, in altri può essere più conveniente un altro:  tra la cartina utilizzata come indice grafico negli orari ferroviari e una cartina stradale, conviene la prima per scegliere le linee ferroviarie con cui raggiungere in treno una località, conviene la seconda per organizzare un viaggio in auto;  per valutare lo stato di salute di una persona come informazione sulla sua temperatura corporea un dato come 38.4 è sufficiente, e è più "leggibile" di un dato come 38.391 , che sarebbe rilevabile con un termometro più sofisticato.

  In genere una disciplina si occupa di modelli riferiti a una particolare area di problemi o di fenomeni: ad esempio la fisica cerca di determinare i fattori e le condizioni che sono all origine dei movimenti dei corpi, della trasmissione dei suoni e della luce, dei fenomeni elettrici, delle caratteristiche dei materiali, e la linguistica cerca di individuare i principali meccanismi attraverso cui, nelle varie lingue, a partire dai suoni vengono formate le parole, le frasi, i discorsi.

  Ciò non vale per la matematica: i modelli matematici vengono applicati alle situazioni più disparate e, proprio per questo, si cerca di caratterizzarli nel modo più generale possibile, riferendosi solo ad altri oggetti matematici  [se abbiamo una tabella di dati che descrive come una grandezza cambia al variare di un'altra, noi sappiamo costruirne il grafico indipendentemente dal tipo di grandezze, sia che siano riferite alla fisica o siano riferite alla geografia o all'economia].

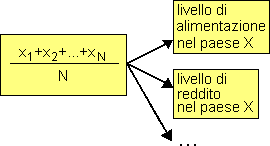
Ad esempio il consumo pro-capite di carne, il reddito medio per famiglia, possono essere interpretati come applicazioni particolari del concetto di media aritmetica, che può essere definito senza riferirsi a carne, abitanti, redditi, ... (clicca l'immagine per ingrandirla)

Il modello "media aritmetica" applicato a diversi contesti

  Anche se i modelli matematici vengono definiti senza riferirsi a fenomeni specifici, sono "nati" in particolari situazioni o attività.
Ad esempio le prime rappresentazioni dei numeri (come sequenze di tacche o cose simili) sono state introdotte per orientarsi nel tempo (tenendo conto del succedersi dei giorni o di altri fenomeni astronomici periodici) e per prime attività contabili (riferite a prede, oggetti e altri beni di sussistenza).  Le operazioni e le prime proprietà aritmetiche si sono poi sviluppate essenzialmente nell ambito delle attività di scambio economico; successiva è stata la loro descrizione in termini astratti; fondamentale, in questo percorso, è stata l'invenzione e la diffusione dell'uso dell'abaco.
Anche a scuola in genere si passa dall introduzione dei concetti matematici in situazioni concrete a una loro definizione formale.
Ad es. si può imparare a sommare e sottrarre valori monetari utilizzando alcune "equivalenze". Se siamo nel 2002 o in un anno successivo, sapendo che [1 euro] equivale a 2 [50 cent], … e conoscendo alcune semplici addizioni (1 e 1 fanno 2, 3 e 4 fanno 7, …) si possono fare gran parte dei calcoli economici elementari:

3 [2 euro] e [50 cent] e [50 cent]   fanno  3 [2 euro] e [1 euro] , cioè  7 [1 euro]
 3  e e   fanno  3 e , cioè  6 e , cioè  7

O, se siamo nel 2000, sapendo che  [100 lire]  equivalgono a 2 [50 lire], … :

3 [100 lire] e [50 lire] e [50 lire]   fanno  3 [100 lire] e [100 lire] , cioè  4 [100 lire]
 3  e e   fanno  3 e , cioè  4

Anche ai nostri giorni molte persone sanno operare solo in questo modo, senza saper rappresentare il calcolo come 6+0.5+0.5=7, o come 300+50+50=400.
Anche noi in situazioni di questo genere procediamo mentalmente in modi simili. Ma per usare le addizioni in altri contesti o per usare una calcolatrice abbiamo dovuto imparare a rappresentare numeri e operazioni anche in "astratto".