Le misure fisiche
 Una misurazione diretta di una grandezza fisica è ottenuta confrontando direttamente
la grandezza con un'altra della stessa specie. Un esempio è la misura di lunghezza di un
oggetto realizzata con una riga graduata, con tacche equidistanziate: la riga viene accostata all'oggetto
e si contano quante tacche stanno tra l'inzio e la fine dell'oggetto.
Una misurazione diretta di una grandezza fisica è ottenuta confrontando direttamente
la grandezza con un'altra della stessa specie. Un esempio è la misura di lunghezza di un
oggetto realizzata con una riga graduata, con tacche equidistanziate: la riga viene accostata all'oggetto
e si contano quante tacche stanno tra l'inzio e la fine dell'oggetto.

Un altro esempio è la misura della massa di un corpo mediante un confronto diretto attraverso una
bilancia a due piatti con un insieme di masse campione.
Una misurazione indiretta di una grandezza è invece ottenuta misurando altre grandezze legate
ad essa da una legge matematica. Un esempio tipico è la misura dell'intensità di una forza mediante il
rilevamento dell'accorciamento di una molla con essa schiacciata: sapendo che, se la forza non è
troppo grande, l'accorciamento della molla è proporzionale alla intensità della forza,
si misura l'accorciamento e da questo si ricava, appunto, l'intensità della forza.
Le bilance a molla (ad esempio quelle impiegate per pesare le persone)
sono poi spesso dotate di un'altro meccanismo di trasformazione: l'accorciamento
della molla provoca una rotazione proporzionale di un dispositivo collegato, per cui quella che si legge
sullo strumento, al posto dell'allungamento della molla, è un angolo di rotazione.
|
Consideriamo, per esempio, una bilancia con il quadrante ripartito in 65
divisioni uguali; ogni divisione rappresenti la variazione di un
chilogrammo, in modo che con la bilancia si possano misurare pesi di al più 65 kg.
Supponiamo che la bilancia abbia la
precisione di 1 kg, cioè che la misura vera possa scostarsi al più
di 1 kg dalla misura letta sul quadrante.
Se, pesando un oggetto, la tacca 44 è quella più vicina alla posizione finale dell'ago, possiamo
concludere che il peso P dell'oggetto (in kg) è compreso tra 44–1=43 e 44+1=45:
43 ≤ P ≤ 45, cioè: P ∈
[43, 45].
Il simbolo "∈"
viene usato come abbreviazione di "appartiene a"
o "sta in" o "è un elemento di"
o …; è una deformazione della lettera "E"
(iniziale di "elemento").
[43,45] è l'intervallo di indeterminazione di P. L'indeterminazione è 45–43 = 2. Non
conosciamo esattamente il numero P, ma conosciamo un'intervallo ampio 2 che lo contiene.
|
 |
| |
 Le misure possono essere a bassa sensibilità
e ad alta sensibilità . Ricordiamo che cosa sono
e come si trattano matematicamente le une e le altre.
Le misure possono essere a bassa sensibilità
e ad alta sensibilità . Ricordiamo che cosa sono
e come si trattano matematicamente le une e le altre.
| Gli strumenti graduati sono in genere costruiti in modo che l'ampiezza di una divisione corrisponda alla sensibilità dello strumento, ossia alla minima variazione della grandezza misurata che fa variare il valore indicato dallo strumento; in questi casi precisione e sensibilità possono essere considerati come sinonimi. Ma non è sempre così: in alcuni casi al più piccolo stimolo che lo strumento percepisce il valore indicato si modifica di più di una divisione; un fenomeno analogo si verifica spesso con gli strumenti in cui le misure sono espresse digitalmente: per misure di un certo ordine di grandezza alla più piccola variazione le ultime cifre variano di molte unità (in questi casi la precisione dello strumento può essere molto maggiore, ossia molto peggiore, rispetto al valore che corrisponde alle variazioni della cifra più a destra), mentre per misure di altri ordini di grandezza lo stesso strumento si può comportare in maniera opposta (l'ultima cifra scatta più lentamente rispetto alle variazioni che lo strumento in realtà percepisce). In alcuni libri di testo viene usato il termine "sensibilità" al posto di quello di "precisione" anche nelle situazioni in cui non è ad esso equivalente. |
|
In fisica spesso si fa una distinzione tra misura
precisa e misura accurata: una misura x
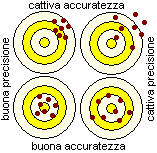
con ideterminazione Δx di una grandezza x è tanto più accurata quanto più x è vicino al valore esatto di x, è tanto più precisa quanto più Δx è piccolo. Questa distinzione rende conto del fatto che, in una attività di misurazione, possono essere presenti degli errori sistematici, dovuti ad un difetto di impostazione [ad esempio l'uso di una bilancia ad ago in cui l'ago a riposo non è posizionato su 0 o di una riga graduata in cui le divisioni sono più ampie del dovuto], che fanno sì che le misure ottenute, per quanto "precise", siano comunque affette da uno scarto dal valore esatto. In questa voce, quando facciamo degli esempi riferiti alla fisica, supponiamo sempre che si tratti di misure accurate, ossia che le approssimazioni siano effettive approssimazioni del valore esatto. La figura a lato illustra metaforicamente il comportamento di apparati misuratori molto sensibili con diversi gradi di precisione e accuratezza (i valori esatti sono il "centro" dei bersagli).
|
 |
Come faccio a eseguire operazioni tra
numeri che conosco solo in modo approssimato? Partiamo da due esempi.
 x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
|
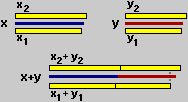 |
Es.: Un
campo di forma triangolare ha lati le cui misure in metri sono a=46,
b=38, c=51. Sappiamo che si tratta approssimazioni con
la precisione di 1 (metro), cioè che, ad essere più
rigorosi: a∈[45,47],
b∈[37,39],
c∈[50,52].
Che cosa possiamo concludere sul perimetro del campo?
a+b+c∈[45+37+50,47+39+52]
= [132,138], cioè: 132 m ≤ perimetro ≤
138 m |
| Possiamo anche scrivere: perimetro = 135 ± 3 m e dire che:
il perimetro è 135 m con la precisione di 3 m |
132 135 138
—+—+—+—+—+—+—+—
|—————|—————|
3 3 |
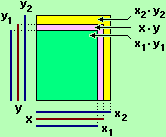
 0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
Es.: Ho
a disposizione i seguenti dati: la popolazione P della
città X è di 89 mila abitanti e il 37.2% di essa ha
più di 50 anni. Qual è il numero A degli
abitanti con più di 50 anni? |
 |
Si tratta di dati arrotondati, cioè:
P ∈ [88.5 mila, 89.5 mila], percentuale ∈ [37.15, 37.25].
Quindi:
A = P·percentuale ∈ [88.5 mila · 37.15%, 89.5 mila · 37.25%] =
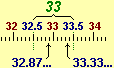
= [32.87775 mila, 33.33875 mila]
|
| Posso dire che A è tra 32 mila 800 e 33 mila 400. Poiché
si tratta di un intervallo contenuto nell'intervallo che
corrisponde all'arrotondamento a 33 mila (vedi figura a lato), per
essere più sintetici, pur perdendo qualche informazione,
posso arrotondare A con 33 mila. |
 |
Nel caso di queste operazioni e delle altre possiamo fare facilmente i calcoli col programmino online
"calcolo approssimato" accessibile QUI:

Rivediamo l'ultimo esempio:
x1 = 88.5 x2 = 89.5 y1 = 0.3715 y2 = 0.3725 [x]
min = 32.87775 max = 33.33875 indet = 0.461 33.10825 ± 0.2305 33.11 ± 0.24
Altro esempio: un'automobile, mentre sta viaggiando a velocità costante, percorre una
distanza di 240 ± 2 m in 12 ± 0.2 s. Qual è la sua velocità?
x1 = 238 x2 = 242 y1 = 11.8 y2 = 12.2 [/]
min = 19.5081967213115 max = 20.5084745762712 indet = 1.0002778549597 [m/s]
Per esprimerci invece in km/h in m/s, tenendo conto che
1 km = 1000 m, 1 h = 3600 s, 1 m/s = 3600/1000 km/h = 3.6 km/h
x1 = 19.5081967213115 x2 = 20.5084745762712 y1 = 3.6 y2 = 3.6 [x]
min = 70.2295081967214 max = 73.8305084745763 indet = 1.0002778549597
72.03000833564886 ± 1.80050013892745
Concludendo: 72 ± 2 km/h (72 km/h con la precisione di 2 km/h)
Questi erano esempi di misure a "bassa sensibilità", ossia che non variano al ripetere della misurazione.
Le misure ad "alta sensibilità" sono quelle che variano al ripetere della misurazione. Un esempio.
Un orologio digitale che visualizza i centesimi di secondo è uno strumento a bassa sensibilità: se (usato nella modalità cronometro) venisse avviato e arrestato facendo trascorrere esattamente sempre lo stesso tempo sul visore si leggerebbe sempre lo stesso valore. Ma se considero, invece del solo orologio, l'apparato uomo+orologio e lo uso per cronometrare lo stesso intervallo di tempo, ogni volta interviene un errore casuale pari alla differenza tra il tempo (casuale) con cui ritardo l'avvio del cronometro e il tempo (casuale) con cui ritardo l'arresto di esso. Ad esempio se avvio e arresto la misurazione man mano che un altro orologio scatta di 1 sec, non troverò, in genere, esattamente 1 sec, ma potrò trovare, via via che ripeto la misurazione,
1.11, 1.03, 1.09, 0.97, 0.99, ...
Ecco i 47 valori in centesimi di secondo ottenuti da una persona misurando manualmente con un orologio il tempo che impiega un altro orologio a scattare in avanti di 1 :s. La misura vera è quindi 1 s. Faccio finta di non conoscerla; vedremo come potremmo cercare di determinarla.
111, 103, 109, 97, 99, 110, 99, 103, 109, 106, 109, 112, 98, 110, 90, 98, 96, 90, 96, 90, 109, 103, 96, 97, 96, 96, 109, 103, 98, 94, 115, 78, 85, 96, 89, 121, 98, 103, 97, 88, 98, 129, 96, 68, 91, 80, 102
Le misure sono troncate ai centesimi di secondo. Per avere i valori arrtondati devo aggiungere mezzo centesimo di secondo:
111.5, 103.5, 109.5, 97.5, 99.5, 110.5, 99.5, 103.5, 109.5, 106.5, 109.5, 112.5, 98.5, 110.5, 90.5, 98.5, 96.5, 90.5, 96.5, 90.5, 109.5, 103.5, 96.5, 97.5, 96.5, 96.5, 109.5, 103.5, 98.5, 94.5, 115.5, 78.5, 85.5, 96.5, 89.5, 121.5, 98.5, 103.5, 97.5, 88.5, 98.5, 129.5, 96.5, 68.5, 91.5, 80.5, 102.5
Rappresento i dati e ne calcolo la media ad esempio con lo script "istogramma" presente QUI:

Ho un istogramma grosso modo simmetrico attorno al valor medio m = 99.8617.
Quale precisione associare a m?
Si può dimostrare che, se ho qualche decina di dati (in questo caso sono N = 47), posso calcolare lo scarto quadratico medio
sqm = √( (111.5-m)²+...+(102.5-m)² ),
calcolare la cosiddetta deviazione standard della media σ = sqm·√(N/(N-1))
e prendere come misura del tempo tra uno scatto e l'altro dell'orologio m ± σ con la probabilità circa del 70%,
m ± 2· σ con la probabilità circa del 95%,
m ± 3· σ con la probabilità circa del 99.7%,
ossia, praticamente, con certezza.
Facciamo i calcoli impiegando "calcolatrice2" presente QUI:

sqm = 10.737537123835274 σ = 1.5831634778241008 3σ = 4.749490433472302
Posso concludere che la misura vera è 99.86±4.75 cs, ovvero 100±5 cs, o che
è 100±1.6 cs al 70%.
 Ora accenniamo a qualche questione legata alla strumentazione che si impiega per effettuare
le misurazioni.
Ora accenniamo a qualche questione legata alla strumentazione che si impiega per effettuare
le misurazioni.
La bilancia pesapersone a molla è un esempio di trasduttore, cioè di dispositivo
che converte un segnale da una forma in un'altra. In questo caso converte il peso della persona
in energia potenziale della molla compressa, che si manifesta attraverso la rotazione dell'ago di lettura
dalla posizione iniziale in una nuova posizione.
Per un altro esempio di trasduzione si pensi alla trasformazione del suono in tensione elettrica, che caratterizza tutti i microfoni
magnetici.
Altri esempi sono offerti dalle strumentazioni per misure elettriche. Ad esempio in un amperometro
analogico, come la corrente passante
per le spire aumenta, lo stantuffo viene attirato ulteriormente nella bobina e il puntatore devia verso destra:
vedi la figura sottostante a sinistra.

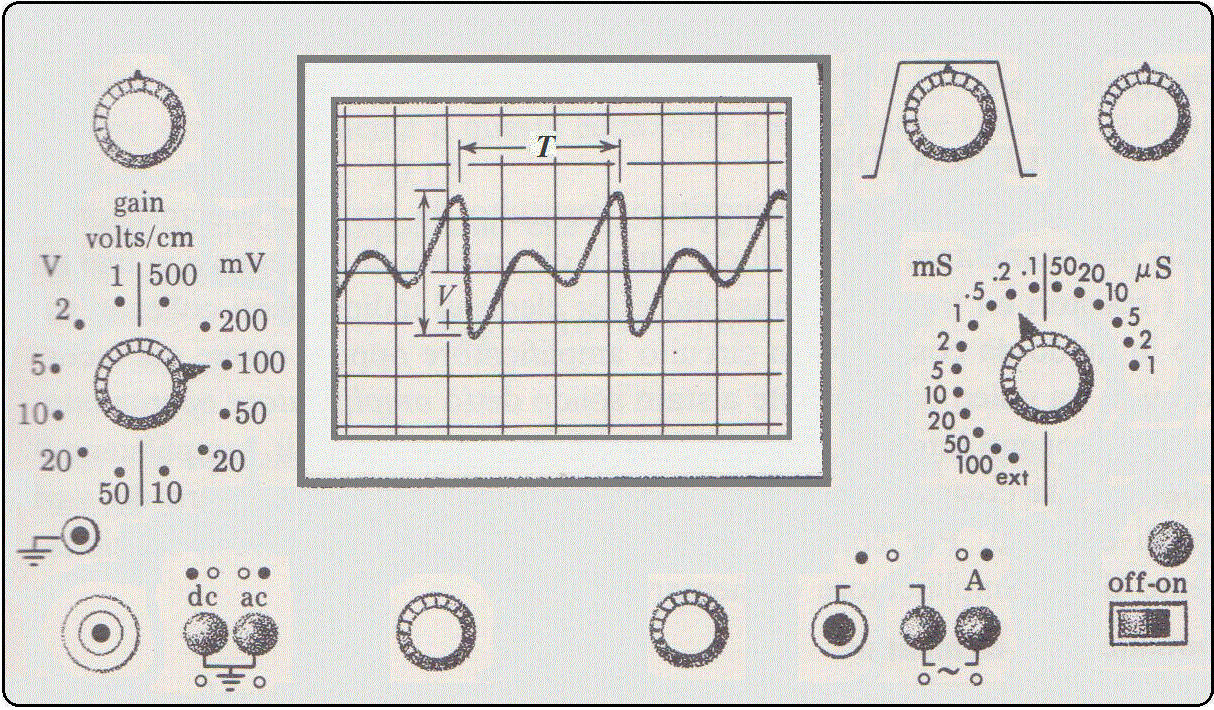
Sopra a destra è raffigurato il pannello frontale di un oscilloscopio, con le principali
manopole di controllo. Un oscilloscopio consente di misurare segnali elettrici che variano rapidamente
nel tempo (sull'asse orizzontale viene rappresentato il tempo, su quello verticale la tensione). Le linee del
reticolo sono distanziate tra di loro di 1 cm.
La manopola a destra regola la velocità di scansione. Nella figura è di 0.2 ms/cm: il
punto luminoso sullo schermo percorre, da sinistra a destra, 1 cm in 0.2 ms, ovvero viaggia a 10/0.2 = 50 m/s.
Il segnale studiato viene inviato all'oscilloscopio (attraverso i terminali) e, quindi, amplificato mediante la
manopola posta a sinistra. Nella figura è posizionata su 100 mV/cm: uno spostamento verticale di 1 cm
sullo schermo corrisponde ad una differenza di potenziale di 100 mV tra i terminali di ingresso.
Nel caso della traccia oscilloscopica sopra raffigurata la tensione V, da picco a picco, è di
0.27 V mentre il periodo T è di 0.6 ms.
 In Fisica, oltre a grandezze che vengono misurate, ve ne sono altre a cui viene assegnato un valore costante a priori. Ve ne sono diverse. Accenniamo solo a due
delle più famose:
In Fisica, oltre a grandezze che vengono misurate, ve ne sono altre a cui viene assegnato un valore costante a priori. Ve ne sono diverse. Accenniamo solo a due
delle più famose:
• la velocità c della luce nel vuoto, pari (esattamente) a 2.99792458·108 m/s (valore fissato nel 1975);
• la costante di Coulomb k, pari (esattamente) a
8.9875517873681764·109 N·m²/C² (N: newton, C: coulomb, m: metri) [8.9875517873681764·109 = 299792458²·10−7]
che è la costante di proporzionalità tra la forza con cui interagiscono due cariche elettriche e il rapporto tra il prodotto delle due cariche e il quadrato
della loro distanza (il valore è stato fissato nel 1948). È più facile ricordare il valore come, circa, 9·109 N·m²/C²
Per un elenco delle principali costanti fisiche vedi qui.
 Una misurazione diretta di una grandezza fisica è ottenuta confrontando direttamente
la grandezza con un'altra della stessa specie. Un esempio è la misura di lunghezza di un
oggetto realizzata con una riga graduata, con tacche equidistanziate: la riga viene accostata all'oggetto
e si contano quante tacche stanno tra l'inzio e la fine dell'oggetto.
Una misurazione diretta di una grandezza fisica è ottenuta confrontando direttamente
la grandezza con un'altra della stessa specie. Un esempio è la misura di lunghezza di un
oggetto realizzata con una riga graduata, con tacche equidistanziate: la riga viene accostata all'oggetto
e si contano quante tacche stanno tra l'inzio e la fine dell'oggetto.


 x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2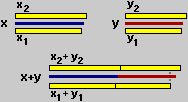
 0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2





