Storia.

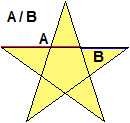
1.  Mentre gli antichi Babilonesi già nel 1800 a.C. non avevano alcuna preoccupazione a rappresentare numeri con più cifre, comunque queste si susseguissero, i Greci, molti secoli dopo, non possedevano la scrittura posizionale dei numeri ed erano convinti che ogni grandezza potesse essere espressa come il rapporto tra due numeri interi, ossia come numero razionale.  Non avevano, per esempio, idea che un numero che al quadrato facesse 2 doveva per forza essere irrazionale.  Furono quindi scioccati quando un discepolo di Piatgora scoprì che nel pentagrammma (stella a 5 punte), il loro simbolo di riconoscimento, il rapporto tra le lunghezze dei segmenti A e B (vedi la figura a destra) non poteva essere espresso con un numero razionale (oggi sappiamo esprimere questo numero, che inzia con 1.61803398874…, con tutte le che vogliamo; tale numero viene chiamato sezione aurea).

2.  Lo script a cui puoi accedere da qui automatizza il calcolo della approssimazione con cui posso conoscere il risultato di una operazione effettuata su dati approssimati.  Il calcolo di 3.14159265.../1.233444555...:

x1 = 3.1; x2 = 3.2; y1 = 1.2; y2 = 1.3
# 2.38461538461538 2.66666666666667
x1 = 3.14; x2 = 3.15; y1 = 1.23; y2 = 1.24
# 2.53225806451613 2.56097560975610
x1 = 3.141; x2 = 3.142; y1 = 1.233; y2 = 1.234
# 2.54538087520259 2.54825628548256

    Posso concludere che il risultato sta in [2.38,2.67], anzi in [2.532,2.561], anzi in [2.5453,2.5483], ….  Andando avanti potrei determinare il risultato con la precisione che voglio, facendo eventualmente il calcolo a mano.
    In questo modo posso calcolare il risultato di qualsiasi operazione tra numeri reali che sappia eseguire sui numeri decimali finiti.  Questo è il modo in cui sono definite le operazioni tra numeri reali.  Sui numeri potenzialmente illimitati operavano già i babilonesi, circa 4000 anni fa,  ma il modo in cui operare tra numeri illimitati qui descritto risale essenzialmente a Cantor, che lo ha definito rigorosamente nel 1871.