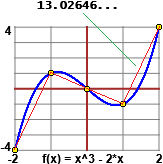
La lunghezza del grafico di una funzione F continua in un intervallo [a,b] può essere calcolata approssimandola con la lunghezza di una spezzata i cui vertici stanno sul grafico della funzione e le cui ascisse sono ottenute dividendo l'intervallo [a,b] in N segmenti uguali, e facendo aumentare via via il numero N.  Vediamo come fare ciò con uno programma in JavaScript nel caso raffigurato a fianco (in cui è considerato il caso N=4), ottenendo per N = 2, 4, 8, ...:     8.94427190999916,     13.026466151931759,     13.291156405311183,     ...  fino a stabilizzarsi su   13.501661653554374.

a=-2; b=2
document.write("la lunghezza della curva tra t=a e t=b<br>")
function x(t) {return t}; function y(t) {return t*t*t-2*t}
n = 2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")

n = n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")

n = n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")

n = n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")

  la lunghezza della curva tra t=a e t=b
  n = 2 L = 8.94427190999916
  n = 4 L = 13.026466151931759
  n = 8 L = 13.291156405311183

Un algortimo più comodo, esemplificato partendo da un "n" maggiore:

a=-2; b=2
document.write("la lunghezza della curva tra t="+a+" e t="+b+"<br>")

function x(t) {return t}
function y(t) {return t*t*t-2*t}
n = 1e5; rip=5
for(k=1; k<=rip; k=k+1) {  n=n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+", L = "+L+"<br>")  }

  la lunghezza della curva tra t=-2 e t=2
  n = 200000, L = 13.501661653242772
  n = 400000, L = 13.501661653477255
  n = 800000, L = 13.50166165353527
  n = 1600000, L = 13.50166165355005
  n = 3200000, L = 13.501661653554594

Lo stesso procedimento si può usare per calcolare la lunghezza di altre curve che non siano il grafico di una funzione.  Queste curve vengono discusse nella successiva voce "rette tangenti e curve".  Vediamo solo, come esempio, come può essere calcolata la lunghezza del cerchio di raggio 1 (ovvero la sua "circonferenza").
Il cerchio può essere descritto come l'insieme dei punti (cos(t), sin(t)) al variare di t tra 0 e 2·π.

     

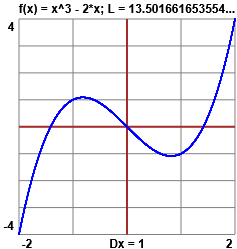
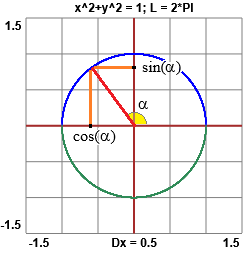
Modifico il programma precedente prendendo come [a,b] l'intervallo [0,2π] e modificando x(t) e y(t):

a=0; b=2*Math.PI
document.write("la lunghezza della curva da t="+a+" a t="+b+"<br>")

function x(t) {return Math.cos(t)}
function y(t) {return Math.sin(t)}
n = 1e6; rip=3
for(k=1; k<=rip; k=k+1) {  n=n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
  L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+", L = "+L+"<br>")  }

  la lunghezza della curva da t=0 a t=6.283185307179586
  n = 2000000, L = 6.283185307179171
  n = 4000000, L = 6.283185307179497
  n = 8000000, L = 6.283185307179542

Abbiamo la conferma che la circonferenza è 2π.