Altre leggi di distribuzione

  Un esempio

    Consideriamo un esempio "fantastico", tratto dalla rivista Scientific American, per introdurre l'impiego di alcune distribuzioni utili ad affrontare alcune situazioni "concrete":

ogni secondo arriva uno zombie di fronte a un muro lungo 1 in cui è praticata un'apertura ampia w. Gli zombie che non passano attraverso l'apertura, dopo la facciata contro il muro si rialzano e si predispongono a ritentare l'avventura, per cui il flusso di zombie è senza fine, e sempre con lo stesso regime.  Inoltre:

(1)   le posizioni lungo il muro in cui arrivano gli zombie hanno distribuzione uniforme (non viene privilegiata alcuna parte del muro), per cui, ovunque sia collocata l'apertura, per essa c'è un flusso stazionario di zombie (la media teorica del numero di zombie N_w che passano in un intervallo di tempo fissato è proporzionale a w:  esiste una costante positiva λ tale che M(N_w) = λ·w);

(2)   la posizione di arrivo di ogni zombie è indipendente da quella di ciascuno dei precedenti, cioè siamo di fronte a un flusso senza memoria;

(3)   è trascurabile la probabilità che due o più zombie arrivino praticamente nella stessa posizione, cioè, al rimpicciolire dell'apertura, la differenza relativa tra Pr(1≤N_w) e Pr(N_w=1) tenda ad annullarsi  (per w → 0 Pr(N_w=1)/Pr(1≤N_w) → 1);  in casi come questo si parla di flusso ordinario.

Si può simulare il fenomeno usando generatore di numeri pseudocasuali ( calc. delle probabilità). Basta indicare con w la ampiezza della apertura e ogni secondo eseguire l'istruzione: if(random(1) < w) U = 1 else U 0 U = 1  indica il passaggio dello zombie per l'apertura        (evento con probabilità  w = AmpiezzaApertura / LunghezzaMuro), U = 0  il non passaggio.

    Infatti il generatore di numeri pseudocasuali verifica (1) e (2), come abbiamo già osservato, e (come si può controllare sperimentalmente) verifica anche (3).

    Sviluppando questa idea è stato realizzato un programma (che non esaminiamo) che simula il fenomeno nel caso in cui w = 1/10. Man mano che arrivano gli zombie esso calcola i tempi di attesa tra un passaggio per l'apertura e il passaggio successivo. Ecco un possibile esito del programma (qualche ora simulata in pochi istanti):

17, 10, 8, 36, 7, 21, 1, 6, 2, 8, 3, 5, 7, 3, 7, 2, 2, 6, 2, 15, 12, 10, 2, 18, 1, 19, 14, 22, 6, 2, 2, 7, 4, 8, 12, 6, 12, 2, 17, 4, 1, 3, 5, 15, 11, 1, 4, 16, 6, 11, 6, 20, 2, 14, 1, 15, 38, 1, 7, 23, 10, 4, 25, 1, 1, 4, 11, 7, 1, 4, 2, 6, 7, 15, 4, 20, 17, 3, 15, 8, 16, 2, 15, 3, 3, 3, 30, 13, 23, 19, 38, 18, 4, 17, 1, 1, 1, 21, 5, 45, 11, 3, 5, 2, 19, 9, 5, 16, 5, 1, 1, 35, 12, 6, 22, 29, 16, 13, 8, 9, 12, 4, 4, 1, 10, 1, 2, 10, 22, 2, 2, 16, 20, 12, 5, 5, 2, 12, 1, 9, 1, 26, 37, 1, 6, 2, 8, 7, 6, 1, 5, 8, 6, 6, 19, 4, 23, 12, 33, 4, 3, 8, 4, 2, 28, 20, 10, 15, 15, 4, 5, 2, 3, 1, 1, 18, 4, 2, 15, 10, 6, 1, 9, 5, 32, 1, 31, 20, 10, 5, 23, 1, 9, 11, 3, 20, 14, 5, 5, 5, 1, 18, 3, 23, 7, 10, 10, 14, 3, 8, 9, 3, 8, 1, 21, 3, 5, 2, 31, 1, 31, 1, 3, 37, 5, 7, 4, 21, 7, 7, 2, 13, 4, 4, 1, 1, 8, 25, 18, 4, 5, 6, 14, 17, 2, 11, 6, 5, 6, 8, 1, 9, 1, 6, 9, 4, 1, 5, 1, 14, 6, 12, 3, 3, 7, 6, 3, 10, 31, 3, 3, 4, 8, 4, 12, 5, 1, 3, 1, 18, 25, 6, 24, 14, 2, 1, 29, 23, 31, 15, 24, 2, 2, 5, 4, 5, 15, 3, 3, 14, 11, 5, 2, 9, 45, 3, 4, 4, 21, 9, 16, 4, 12, 17, 12, 4, 14, 3, 4, 20, 5, 8, 8, 6, 21, 19, 4, 5, 5, 5, 28, 18, 9, 10, 3, 12, 2, 2, 4, 15, 2, 7, 3, 4, 8, 6, 10, 14, 7, 14, 13, 9, 4, 5, 12, 1, 3, 4, 14, 8, 1, 6, 3, 16, 1, 6, 9, 2, 3, 6, 21, 15, 2, 20, 18, 9, 7, 3, 5, 7, 18

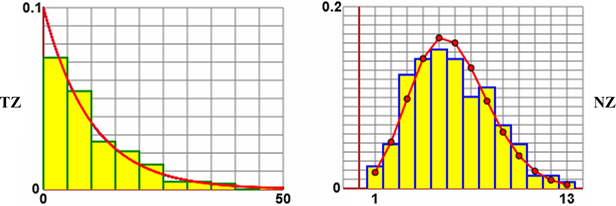
    Sotto a sinistra questi esiti analizzati con lo script "istogramma" (vedi):

←   tempi di attesa     |     quanti zombi   →

    Se calcoliamo quanti zombie passano per l'apertura in 60 secondi otteniamo (simulando per qualche ora):

9, 8, 7, 4, 8, 3, 3, 8, 3, 3, 6, 7, 2, 3, 4, 9, 4, 10, 1, 4, 3, 7, 4, 7, 9, 4, 10, 5, 4, 3, 4, 3, 9, 4, 5, 6, 2, 3, 9, 5, 4, 7, 6, 8, 6, 1, 7, 1, 11, 8, 6, 5, 5, 7, 6, 9, 6, 6, 5, 7, 4, 4, 7, 5, 5, 6, 3, 9, 8, 5, 4, 3, 7, 10, 8, 1, 4, 6, 7, 6, 11, 8, 6, 8, 7, 9, 3, 6, 10, 5, 6, 6, 2, 3, 8, 4, 1, 9, 5, 4, 6, 8, 3, 3, 5, 13, 10, 4, 7, 4, 7, 6, 7, 3, 6, 8, 9, 4, 11, 10, 3, 9, 7, 8, 4, 8, 9, 3, 5, 9, 3, 11, 2, 9, 4, 5, 4, 8, 5, 8, 4, 4, 4, 7, 7, 5, 6, 12, 2, 4, 6, 4, 5, 6, 5, 10, 5, 10, 9, 6, 4, 8, 12, 6, 5, 5, 7, 6, 7, 4, 9, 2, 10, 7, 3, 6, 5, 5, 6, 6, 3, 6, 7, 5, 8, 8, 3, 8, 5, 3, 3, 2, 3, 6, 4, 9, 9, 6, 3, 10, 8, 4, 5, 3, 12, 5, 6, 4, 13, 2, 10, 5, 5, 7, 7, 8, 1, 9, 4, 8, 1, 2, 8, 8, 6, 7, 3, 3, 5, 6, 5, 10, 9, 8, 3, 6, 5, 5, 6, 5, 7, 2, 10, 4, 5, 3, 8, 5, 6, 6, 3, 5, 4, 6, 7, 2, 8, 4, 8, 12, 3, 8, 3, 4, 5, 6, 3, 2, 4, 6, 5, 5, 4, 6, 4, 4, 8, 5, 5, 7, 5, 5, 8, 2, 7, 3, 2, 10

    Con lo stesso script analizziamo questi dati, con l'esito riportato sopra a destra.

    Come si vede, l'istogramma a sinistra, dei tempi di attesa, ha, grosso modo, andamento decrescente, simile all'istogramma della () distribuzione esponenziale negativa.  Quello degli zombi che passano ogni minuto ha un andamento a campana asimmetrica, che ha qualche somiglianza con una binomiale (). Nel prossimo paragrafo approfondiremo lo studio di questa somiglianza.

  Le leggi esponenziale e di Poisson

    Diamo alle due sequenze di dati i nomi TZ (tempi tra 2 passaggi quando l'apertura è w = 1/10) e NZ (corrispondente numero di passaggi in 1 min).  Analizziamole anche con "calcolatrice2" (presente qui):

•  L'analisi di TZ, in cui media e deviazione standard sono quasi uguali, rafforza l'idea che la differenza temporale Dw tra due successivi passaggi per l'apertura abbia distribuzione esponenziale negativa, come nel caso dei tempi di attesa tra una telefonata e l'altra nella situazione considerata nella scheda leggi di distribuzione (variabili continue).

    Si può dimostrare teoricamente che, nelle ipotesi fatte, Dw ha effettivamente funzione di densità x → w·exp(-w·x) con w = ampiezza della apertura del muro, cioè con 1/w = tempo di attesa medio (in sec). Vedi la figura seguente a sinistra.

•  L'andamento dell'istogramma di NZ è simile a quello di una binomiale non simmetrica. In realtà si può dimostrare che, fissata una durata di tempo T (in sec), il numero di zombie Nw che passano per l'apertura in un intervallo di tempo ampio T ha legge di distribuzione:

Pr(Nw = n) =	an	e–a		con  a = numero medio di zombie che passano per l'apertura nel tempo T
	——
	n!

Poiché nel nostro caso T = 60,  a = wT = 6.  Vedi la figura sopra a destra (in cui si è considerato solo n tra 1 e 13, in corrispondenza degli esiti sperimentali).

    È una funzione (di n) che all'inizio sale quasi esponenzialmente, poi scende, quando n! prevale su aⁿ.  Essendo una legge di distribuzione abbiamo:

Pr(Nw=0) + Pr(Nw=1) + Pr(Nw=2) + … = 1,  e quindi:
e^−a · (1 + a + a²/2 + a³/3! + a⁴/4! + …) = 1.  Dunque dev'essere:
1 + a + a²/2 + a³/3! + a⁴/4! + … = e^a.

    Avevamo già visto che, per x → 0, e^x ≈ x + 1.  In effetti si può dimostrare che vale anche  e^x ≈ x + 1 + x²/2,  anzi che  e^x ≈ x + 1 + x²/2 + x³/3!   e così via.  Non vedremo qui la dimostrazione di questo fatto.

    Osserviamo che Pr(Nw=0), valore che esprime la probabilità che non passino zombie, deve essere uguale a Pr(Dw>T), cioè alla probabilità che la differenza temporale tra due passaggi sia maggiore di T.

    Verifichiamolo:  Pr(Nw=0) = e^-a;  Pr(Dw>T) = 1 - Pr(Dw≤T) = 1-(1-e^-wT) = e^-wT = e^-a.

    Questa legge di distribuzione si chiama legge di Poisson (di parametro a - spesso il parametro viene indicato con la lettera greca λ, "lambda").

    Si può dimostrare che  M(Nw) = Var(Nw) = a.  Ciò è in accordo con gli esiti sperimentali, riportati sopra, quando a valeva 6:

  Ancora sulla legge esponenziale

    Un fenomeno che si distribuisca come i tempi di arrivo del fenomeno sopra considerato dà luogo ad un istogramma che tende ad assumere la forma del grafico di una funzione esponenziale f: x → w·exp(-w·x), con w = 1/10.  Sotto, a destra, è rappresentato il grafico della funzione g che è la corrispondente ripartizione, ossia g: x → ∫_[0,x]f.

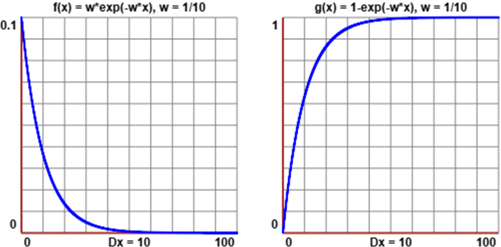
    Qual è l'espressione analitica di questa funzione di ripartizione g?
    Sappiamo che è ancora una funzione esponenziale.  Infatti  d exp(x)/dx = exp(x), quindi  d exp(k·x)/dx = k·exp(k·x), e quindi  d exp(-w·x)/dx = -w·exp(-w·x).
    Quindi g(x) = ∫_[0,x]f = ∫_[0,x]w·exp(-w·t) dt = -exp(-w·x) + exp(-w·0) = 1 - exp(-w·x)

Esercizio 1   (soluzione)

  Ancora sulla legge di Poisson

All'aumentare del parametro la "poissoniana" tende ad assumere andamento simmetrico a campana. Si vedano i grafici a destra, relativi ad a = 6 e a = 12.     Abbiamo già osservato che la curva poissoniana assomiglia a una binomiale. In effetti si può dimostrare che la legge di Poisson approssima la legge binomiale Bn,p con n·p = a, e che, fissato a, questa approssimazione migliora al crescere di n  (la poissoniana, quindi, come la bernulliana, tende a confondersi con una curva di Gauss, e con questa spesso può essere approssimata).     In altre parole l'approssimazione migliora man mano che p (=a/n) tende a 0, cioè più è raro l'evento di cui conto il verificarsi nelle n prove ripetute. Per questo a volte la legge di Poisson viene anche chiamata legge degli eventi rari.

  L'impiego della legge di Poisson è frequente. Infatti sono molte le situazioni che si comportano analogamente alla situazione degli "zombie", cioè in cui si ha a che fare con:

(1)   elementi che si distribuiscono uniformemente in un certo "spazio",

(2)   cadendo in modo stocasticamente indipendente in sottospazi disgiunti, e

(3)   tendenzialmente, senza sovrapporsi.

e si vuole valutare la probabilità che cada una certa quantità di elementi in una porzione di spazio di dimensione w fissata, noto il numero medio a di elementi che cadono in una porzione di dimensione w.

Esempio. Una lamiera presenta dei piccoli difetti che si collocano in modo che soddisfa le condizioni sopra descritte, con densità di 0.03 difetti per cm². La probabilità che un pezzo di 10 cm² abbia almeno un difetto è: 1-Pr(Nw=0) = 1-exp(-a) = 1-exp(-0.3) = 0.259; infatti a = 0.03·10 = 0.3.

  Anche le situazioni di "eventi rari" possono essere interpretate in questo modo.
    Consideriamo, ad esempio, un campione radioattivo che contenga 2.5 10²¹ nuclei; ogni nucleo abbia, in ogni istante, la probabilità 5.2 10^-21 di decadere entro 1 minuto; vogliamo trovare qual è la probabilità che il numero N dei decadimenti in un minuto sia 2. Dovremmo assegnare ad N la legge B_n,p con n=2.5 10²¹ e p=5.2 10^-21 (n è praticamente costante), ma ci troveremmo di fronte ad elevamenti alla potenza proibitivi.
    Per quanto osservato sopra possiamo approssimare questo valore usando la legge di Poisson con a = np = 13:  Pr(N=2) = 13²/2·e^-13=1.91 10^-4.  Ma anche senza passare attraverso la binomiale potevano osservare che gli atomi decadono in tempi che si succedono rispettando le condizioni (1) (3) (ad esempio la (1) corrisponde al fatto che l'emissione di elettroni è più o meno costante),  e che il numero medio (a) di nuclei che decadono nel tempo di 1 minuto (w) è np.

Esercizio 2   (soluz.)       Esercizio 3   (soluz.)