 Confronto tra infiniti
Confronto tra infinitiDue cineclub, Ca e Cb, presentano le seguenti tariffe: il primo 10 € di tessera annuale
più 3 € a spettacolo; il secondo
Studio in generale la situazione rappresentando il costo totale annuo con dei grafici.
Siano A(n) e B(n) i costi annuali per, rispettivamente, Ca e
Cb se vi vedo n film. Ho (facendo variare nel grafico per semplicità n tra i numeri reali):
A(n) = 3·n+10
B(n) = 3·n+16
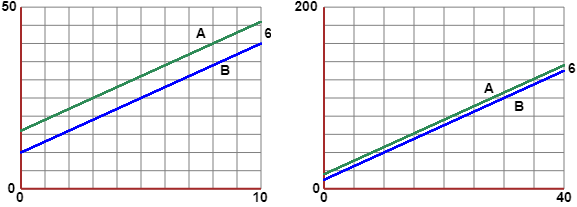
Al crescere del numero di film visti, i costi totali tendono entrambi all'infinito, mantenendo una differenza costante di 6 €.
Ma la distanza tra i due grafici tende ad essere trascurabile rispetto al valore delle ordinate:
se vedo molti spettacoli non c'è praticamente differenza tra quanto spenderei complessivamente nei due cineclub.
Il fatto che A(n) e B(n) tendono ad essere "praticamente" uguali possiamo esprimerlo dicendo che il rapporto tra essi,
Per descrivere quanto messo ora in luce si usa dire che, al crescere
di n, A(n) e B(n) sono asintoticamente uguali (o equivalenti);
in simboli:
Posso precisare questo modo di dire usando il concetto di
 limite
limite
limx → α F(x) / G(x) = 1
| Nel nostro caso, per n → ∞: |
|
Nota. Nel caso del nostro esempio iniziale, ovviamente, nella realtà non ha senso
far tendere a ∞ il numero n degli spettacoli visti in un anno.
Al massimo n potrà valere qualche centinaio, se il cineclub è aperto tutti i giorni.
Tuttavia è comodo astrarre dalla situazione e far finta che ciò possa
accadere:
pensando ai termini A(n) = 3n + 10 e B(n) = 3n + 16 e al loro comportamento per
• Per x → ∞ i grafici delle funzioni tendenti a ∞ x → 2x+2 e x → 2x-7 "tendono a confondersi" con quello di
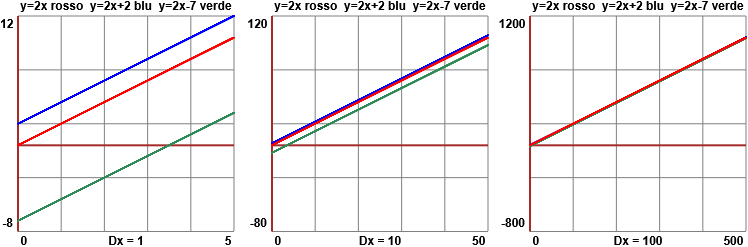
Il motivo di ciò è che, per x → ∞, i contributi dei termini 2 e -7 tendono a diventare trascurabili rispetto al valore complessivo di, rispettivamente, 2x+2 e 2x-7. È una situazione analoga a quella di At(x) e di Bt(x) dell'esempio iniziale. E infatti:
|
|
| •
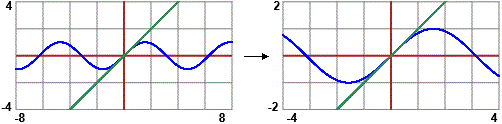
Se traccio il grafico di F: x → (sin(x) + x/2)² ottengo una
rappresentazione come quella qui a destra: una curva che oscilla con apparente andamento parabolico. Provo a confrontare, per | 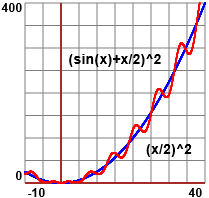 | ||||||||||||||
| |||||||||||||||
| |||||||||||||||
| [ per x→∞ sin(x)/x → 0 in quanto è compreso tra 1/x e −1/x entrambi i quali tendono a 0, e il passaggio al limite conserva la relazione "≤" ] | |||||||||||||||
| Dunque: per x → ∞ F(x)/x2 → (1/2)2 = 1/4, e
quindi F(x) / (x2/4) → 1. Posso concludere che, per x → ∞, F(x) ≈ x2/4. |
 La parola asintoticamente richiama il termine asintoto
La parola asintoticamente richiama il termine asintoto
 figure 2, figure 2,Si noti, tuttavia, che non è detto che se due funzioni f1 e f2 hanno grafico con uno stesso asintoto si abbia che • H(x)/K(x) = 1/x / (1/x²) = x che non tende a 1, ma a 0; in altre parole, 1/x² all'avvicinarsi di x a 0 cresce più velocemente di 1/x, per cui i due numeri assumono rapidamente ordini di grandezza molto diversi, non tendono ad essere uguali (pur tendendo entrambi a ∞); • H(x)/L(x) → 3 ≠ 1, ovvero H(x) ≈ 3·L(x). | 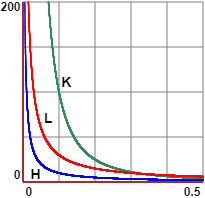 |
Quanto valgono h e k nei due casi seguenti?
√(x8+x) + 7·x8 ≈ h·xk per x → 0
√(4·cos(x)+9·x6 ) ≈ h·xk per x → ∞
− per x → 0 x8 va a 0 più velocemente di x, quindi √(x8+x)+7·x8 va a 0 come √x;
quindi h = 1, k = 1/2;
− per x → ∞ 4·cos(x) è trascurabile rispetto a 9·x6, quindi
√(4·cos(x)+9·x6 ) va a ∞ come 3·x3;
quindi h = 3, k = 3.
Verifica usando WolframAlpha:
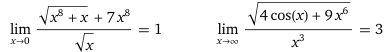
Approfondiamo quanto visto con i precedenti esempi.
 Sostituire un termine con un altro asintoticamente equivalente è molto spesso comodo per determinare limiti del tipo
Sostituire un termine con un altro asintoticamente equivalente è molto spesso comodo per determinare limiti del tipo 
Esempio: limx → ∞ (sin(x) + x/2)² / (3 + 2x²)
Sia (sin(x) + x/2)² che 3 + 2x² tendono a ∞, quindi siamo in un caso "∞/∞".
Abbiamo visto  che, per x→∞, (sin(x) + x/2)² ≈ x²/4.
che, per x→∞, (sin(x) + x/2)² ≈ x²/4.
3 + 2x² ≈ 2x². Infatti (3+2x²)/(2x²) = 3/(2x²) + 2x²/(2x²) = 3/(2x²) + 1 → 0+1 = 1.
Quindi:
limx → ∞ (sin(x) + x/2)² / (3 + 2x²) = limx → ∞ x²/4 / (2x²) = limx → ∞ 1/4/2 = 1/8.
 Siano F(x) e G(x) tendenti all'infinito per x → α. Se F(x) ≈ G(x)
si scrive anche, convenzionalmente,
F(x) =
Siano F(x) e G(x) tendenti all'infinito per x → α. Se F(x) ≈ G(x)
si scrive anche, convenzionalmente,
F(x) =
per x → α F(x) è uguale a G(x) a meno di un termine trascurabile rispetto a G(x)
Facendo riferimento ad alcuni degli esempi visti sopra possiamo dunque scrivere:
• per x → ∞, 2x + 7 = 2x + … : per → ∞, 7 è trascurabile rispetto a 2x.
• per x → 0, x + 1/x = 1/x + … : per → 0, x è trascurabile rispetto a 1/x.
• per x → ∞, sin(x) + x2 = x2 + … : per → ∞, sin(x) è trascurabile rispetto a x2.
Calcoliamo velocemente lim x → ∞ (x + 3 x²) / x².
Per x → ∞ x + 3 x² ≈ 3 x², ovvero
x + 3 x² = 3 x² + … Quindi:
lim x → ∞ (x + 3 x²) / x² =
lim x → ∞ 3 x² / x² = 3.
|
In generale, per x → ∞ xh è trascurabile rispetto a xk se 0 < h < k. Vedi il grafico qui a destra. Quando F(x) è un infinito trascurabile rispetto a G(x) si dice anche che F(x) è un infinito di ordine inferiore rispetto a G(x). Quindi, per x → ∞, x² è trascurabile rispetto a x³. Un altro esempio di limite: lim x → ∞ (√x + x3 + x – 130) / (3x3 + 2). √x + x3 + x – 130 ≈ x3 in quanto √x, x e –130 sono tutti trascurabili rispetto a x3.
Analogamente 3x3 + 2 ≈ 3x3. Quindi il limite equivale a: | 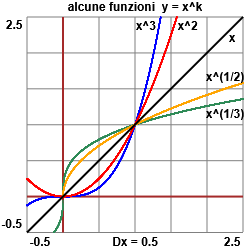 |
 Quando, per x → α, F(x) e G(x) tendono all'infinito e F(x) ≈ k·G(x), ossia
Quando, per x → α, F(x) e G(x) tendono all'infinito e F(x) ≈ k·G(x), ossia
Abbiamo appena visto che √x + x3 + x – 130 e 3x3 + 2 per x → ∞ sono infiniti dello stesso ordine.
Considerazioni e definizioni analoghe si hanno per il caso in cui F(x) e G(x) per x → α (finito o infinito) tendano a 0, ossia siano degli infinitesimi.
Di fronte a lim x → 0 (x2+3x)/(2x+5x4), che è del tipo "0/0", cerchiamo di capire come si possono approssimare x2+3x e 2x+5x4 quando x è vicino a 0.
I grafici che seguono mettono in luce che, per x→0, x2+3x e 3x tendono a confondersi, ovvero in 0 hanno la stessa pendenza, ovvero y=3x è la retta tangente a x2+3x per x=0 (la retta tangente al grafico di una funzione F per x=p è tra le rette passanti per (p,F(p)), quella che "meglio approssima" il grafico). La cosa del resto è facimente verificabile usando la derivazione (vedi):
D x=0 (x²+3x) = (2x+3) x=0 = 3, e la retta per (0,0) con pendenza 3 è y = 3x.
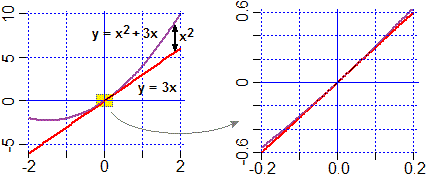
Anche in questo caso posso osservare che per x → 0
(x²+3x)/(3x) = x/3+1 → 1
ed esprimere ciò dicendo che x²+3x equivale asintoticamente a 3x:
x²+3x ≈ 3x (scrivo anche x²+3x = 3x + … per indicare la presenza di un termine trascurabile rispetto a 3x, per x → 0).
Analogamente per x → 0
(2x+5x4)/(2x) = 1+5/2·x3 → 1, ovvero
2x+5x4 equivale asintoticamente a 2x:
2x+5x4 ≈ 2x.
Dunque lim x→0 (x2+3x) / (2x+5x4) = lim x→0 3x / (2x) = lim x→0 3/2 = 3/2.
|
Se per x → α F(x) è trascurabile rispetto a G(x) si dice anche che F(x) è un infinitesimo di ordine superiore rispetto a G(x).
Si dice che sono infinitesimi dello stesso ordine se
G(x)/F(x) = 1/x2/(1/x) = 1/x → 0 per x → ∞ :
1/x2 al crescere di x si avvicina a 0 più velocemente di 1/x, ossia è un infinitesimo di ordine trascurabile per H(x)/F(x) → 3, ovvero H(x)/(3·F(x)) → 1, ovvero H(x) ≈ 3F(x) per x → ∞. | 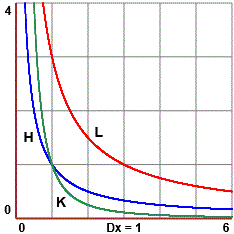 |
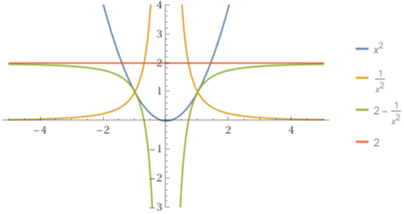
Per inciso, osserviamo, con la figura seguente realizzata con plot x^2, 1/x^2, 2-1/x^2, 2, x=-5..5, y=-3..4
mediante WolframAlpha, che usando i concetti di estremo inferiore, o "inf", e di estremo superiore,
o "sup" (
 Ovviamente, limx → 0 sin(x) = 0, essendo sin continua.
Ovviamente, limx → 0 sin(x) = 0, essendo sin continua.
Per caratterizzare il modo in cui sin(x) tende a 0, osserviamo che per
function F(x) {return Math.sin(x)/x} x=1; for(i=0; i<8; i=i+1) {x=x/10;document.write(F(x),"<br>")} |
0.9983341664682815 0.9999833334166665 0.9999998333333416 0.9999999983333334 0.9999999999833332 0.9999999999998334 0.9999999999999983 1 |
 Sostituire un termine con un altro asintoticamente equivalente è comodo per determinare anche limiti del tipo "
Sostituire un termine con un altro asintoticamente equivalente è comodo per determinare anche limiti del tipo "
• Esempio: limx → 0 (sin(x) + x/2) / (2x + x2)
Sia (sin(x) + x/2) che 2x+x2 tendono a 0, quindi sono in un caso "0/0".
So che, per x→0, sin(x) = x+o(x), da cui sin(x)+x/2 = 3x/2+... ≈ 3x/2, e che, per x→0, 2x+x2 ≈ 2x. Quindi:
limx → 0 (sin(x) + x/2) / (2x + x2) = limx → 0 3x/2 / (2x) = limx → 0 3x/(4x) = 3/4.
• Un altro es.: lim x→∞ (sin(1/x)+1/x2) / (1/x)
Poichè 1/x → 0 per x → ∞, siamo in un caso "0/0".
È comodo  limiti]
limiti]
limu → 0 (sin(u) + u2) / u
Per u → 0, sin(u) ≈ u, quindi sin(u)+u2 ≈ u+u2 ≈ u (in quanto u2 va a 0 più, velocemente di u). Dunque:
limu → 0 (sin(u) + u2) / u = limu → 0 u / u = limu → 0 1 = 1
• Ancora un es.: lim x→1 ((x-1)2+(1-x)3+√(x2-1)) / ((1-x)-(x-1)4)
Innanzi tutto osservo che considero x→1+ (per x<1 √(x2-1) non è definito) e che si tratta di un caso "0/0".
√(x2-1) = √((x-1)(x+1)) ≈ √(x-1)√2 = √2(x-1)1/2
(x-1)2 e (x-1)3 vanno a 0 più velocemente di (x-1)1/2
e quindi (x-1)2+(1-x)3+√(x2-1) ≈ √2(x-1)1/2
Inoltre (x-1)4 va a 0 più velocemente di x-1 per cui (1-x)-(x-1)4 ≈ 1-x = -(x-1)
Concludendo, mi riconduco a:
limx → 1+ -(√2(x-1)1/2) / (x-1) = limx → 1+ -√2 / (x-1)1/2 = -√2 / 0+ = –∞
Potevo valutare il limite soprastante anche osservando direttamente che (x-1)1/2/(x-1) → ∞ per x → 1+ in quanto (x-1) è un infinitesimo di ordine superiore rispetto a (x-1)1/2.
A destra la conferma con le uscite del seguente programma in JavaScript (che calcola le uscite per x = 1.1, 1.01, 1.001, ...): with (Math) { function F(x) {return (pow(x-1,2)+pow(1-x,3)+pow(x*x-1,1/2)) / ((1-x)-pow(x-1,4))} h=1; for(i=0;i<8;i=i+1) {h=h/10; document.write(F(1+h),"<br>") } } |
-4.667907787168669 -14.187332691425121 -44.73353744795809 -141.42499171686723 -447.21472353107634 -1414.2139170160428 -4472.136065508048 -14142.13566671516 |
• Per x → ∞, (x3 – 2x2 + 2)/(x + 1) + x2 – x = (x3+...)/(x+...) + x2 + ... ≈ x3/x + x2 = x2 + x2 = 2x2
• Per x → 0, (sin(x) + tan(x))2 = (sin(x) + sin(x)/cos(x))2 ≈ (x + x/1)2 = 4x2 (in quanto cos(x) → 1)
• Attenzione.
È errato procedere così: per x → 0
sin(x) + x3 - x = x + ... + x3 - x =
x3 + ... ≈ x3
Infatti sostituendo "sin(x)" con "x + ..." abbiamo inteso che "..." andasse a 0 più velocemente di x non di x3.
Vedremo in una voce successiva (e verificheremo nel prossimo esercizio) che sin(x)-x ≈ -x3/6.
• Attenzione.
È errato procedere così: per x → ∞
Infatti non è detto che se F(x) ≈ f(x) e G(x) ≈ g(x) allora
F(x)G(x) ≈ f(x)g(x)
Vedremo in una voce successiva (e verificheremo nel prossimo esercizio) che per x → ∞
| Di fronte a lim x → 0 (cos(x) – 1) / (sin(x)2 + tan(x)2), che è del tipo | |
|
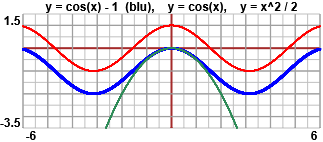
sin(x)2+tan(x)2 ≈ x2 + x2 = 2x2 Per il primo termine del rapporto, Cercando di ripetere quanto fatto  sopra per studiare come si comporta sin(x) per x→0,
vediamo come approssimare il grafico di sopra per studiare come si comporta sin(x) per x→0,
vediamo come approssimare il grafico di In questo caso sembra che l'andamento vicino a x = 0 sia più o meno quello di una parabola, ossia il grafico di una funzione del tipo Studiamo sperimentalmente (con una calcolatrice o un programma) il limite per x → 0 |
 |
|
Con un programmino in JavaScript (che calcola le uscite per x = 1/2, 1/4, 1/8, ...):
with (Math) { function F(x) {return (cos(x)-1)/(x*x) } x=1; for(i=0;i<14;i=i+1) {x=x/2; document.write(F(x),"<br>") } } |
-0.48966975243850897 -0.49740125262968427 ... -0.49999999022111297 -0.49999999813735485 -0.5 -0.5 |
Ovvero, con la "calcolatrice" accessibile da qui:

Metto (cos(A)-1) / (A*A) in (2) e 1e-1 in A e clicco [=],
poi metto 1e-2 in A e clicco [=], poi 1e-3, ...
Ottengo le uscite: -0.49958347219741783, -0.4999958333473664, -0.49999995832550326, ...
Dalle uscite si può congetturare che il limite sia –1/2. Si può effettivamente dimostrare che:
| per x → 0, cos(x) – 1 ≈ –x2/2, ovvero: | cos(x) – 1 | → | 1 | |
| ————— | – | — | ||
| x2 | 2 |
Abbiamo visto questa importante approssimazione di cos(x) (≈ 1-x²/2). Ma potevamo studiare direttamente il limite della funzione iniziale, ad esempio con la "calcolatrice" considerata sopra:
Metto ((cos(A) - 1) / (pow(sin(A),2) + pow(tan(A),2) ) in (2) e 1e-1 in A e clicco [=],
poi metto 1e-2 in A e clicco [=], poi 1e-3, ...
Ottengo le uscite: -0.2493708292868594, -0.24999374958340134, -0.24999993749604257, ...
| Potevo anche utilizzare direttamente WolframAlpha: | ||
| (cos(x) - 1) / (sin(x)^2 + tan(x)^2) as x -> 0 | → | 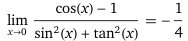 |