Anche senza tracciare il grafico di x → x2–2x–3, poiché x2–2x–3 è fattorizzabile come (x+1)(x–3) (infatti x2–2x–3 diviso x+1 fa x–3 con resto 0), posso concludere che esso interseca l'asse x per x= –1 e x=3. Infatti:
    (x–3)(x+1) = 0  equivale a  x–3 = 0 OR x+1 = 0  e quindi a  x = 3 OR x = –1

    Viceversa, se so che la funzione polinomiale x → A(x) ha grafico che interseca l'asse x per x=h, cioè se so che A(h)=0, posso concludere che A(x) è divisibile esattamente per x–h?
    Ad es. a lato è tracciato il grafico di x → 2x2+5x+3. Esso interseca l'asse x in due punti che hanno ascissa –1 e –1.5 rispettivamente.
    Posso concludere che 2x2+5x+3 è fattorizzabile come (x–(–1))·(…), cioè come (x+1)·(…)? Ovvero come (x–(–1.5))·(…), cioè come (x+1.5)·(…)?

    

    La risposta è affermativa, infatti vale la seguente proprietà, nota come teorema del resto (o di Ruffini):

la divisione di A(x) per  x – h  ha come resto il numero  A(h)

La dimostrazione di ciò è facile.
  Se Q(x) e R sono il quoziente e il resto della divisione di A(x) per x–h:
      A(x) / (x-h) = Q(x) + R / (x-h), ovvero:  A(x) = Q(x)(x–h) + R.
  Quindi, per x=h, A(h) = Q(h)(h–h) + R = 0+R = R

    Come immediata conseguenza del teorema del resto, abbiamo che:

se  A(h) = 0  il polinomio A(x) è divisibile esattamente per  x – h

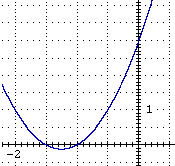
    Nel caso dell'esempio precedente (2x2+5x+3, che si annulla per x=–1 e per x=–3) abbiamo effettivamente che 2x2+5x+3 si divide esattamente per x+1, e dà 2x+3; ovvero che si divide esattamente per x+1.5 e dà 2x+2. D'altra parte (x+1)(2x+3) = 2x2+5x+3 e (x+1.5)(2x+2) = 2x2+5x+3 [si noti che: (2x+3) = 2(x+1.5) e che (2x+2) = 2(x+1)].

    Il teorema del resto ci consente di concludere che, se un'equazione polinomiale ha, ad esempio, 5 soluzioni a, b, c, d ed e, il polinomio è divisibile [sottointeso "esattamente"] per (x–a), (x–b), (x–c), (x–d) e (x–e) e, quindi, è equivalente a (x–a)(x–b)(x–c)(x–d)(x–e)·… . Il polinomio deve, perciò, essere almeno di 5° grado.
    Un'equazione polinomiale di 4° grado, quindi, ha al più 4 soluzioni: se ne avesse 5 dovrebbe essere di grado maggiore di 4.
    In generale possiamo concludere che:

una equazione polinomiale di grado n ha al più n soluzioni.

    Questo risultato, assieme al fatto che le funzioni polinomiali sono continue, ci fornisce argomentazioni teoriche che ci possono indirizzare nella ricerca delle soluzioni di una equazione polinomiale, che può essere fatta sia con metodi numerici o grafici, sia con tecniche algebriche.