Prime figure

  Ricordiamo, in modo intuitivo, il significato e alcune proprietà di alcune semplici figure con cui si ha a che fare spesso nella vita di tutti i giorni.  Sulla geometria  (parola che, come la parola geografia, deriva dalla parola greca "geos" che significa "terra", oltre che dalla parola "metron" che significa misura)  ci soffermeremo più a lungo in varie voci successive (rapporto, proporzionalità, diagrammi, pendenza, ..., spazio, figure 1, ... - vedi anche "esercizi per la scuola di base" in fondo alle varie voci).

  Consideriamo le seguenti immagini.

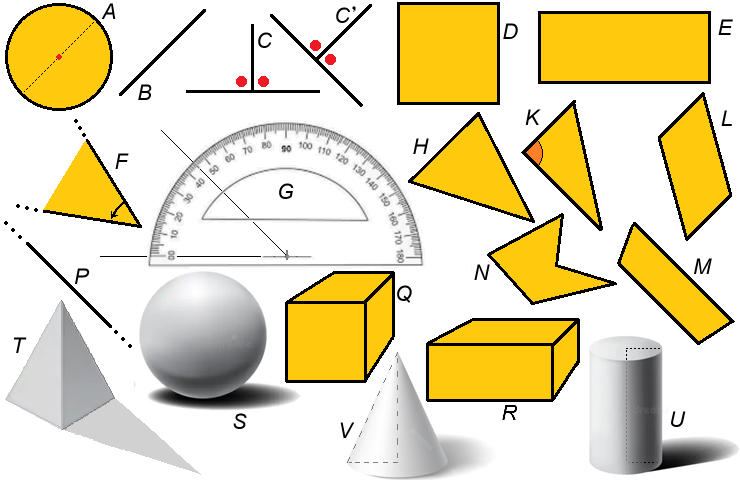
A è un cerchio, tracciabile con un compasso. Nella figura ne sono traccati anche il centro e un diametro, che congiunge, passando per il centro, due punti opposti.  La lunghezza di un cerchio si chiama circonferenza. Come succede per quasi tutte le figure, con lo stesso nome (cerchio) si può indicare anche la sua parte interna  (in qualche libro scolastico italiano viene chiamato circonferenza anche il bordo del cerchio, con lo scopo di usare un nome diverso da quello per la sua parte interna; questa buffa distinzione di nomi per parte interna e bordo non viene più fatta per tutte le altre figure!).

B è un segmento; i punti alle estremità di esso si chiamano estremi.  C rappresenta un segmento che è diretto come il filo a piombo e cade in mezzo ad un altro segmento orizzontale, dividendo lo spazio in due angoli uguali, chiamati angoli retti (sono gli angoli di un comune tavolo da cucina, o quelli da cui vengono battuti i "calci d'angolo");  si dice che il primo segmento (C) è perpendicolare al secondo.  L'aggettivo "perpendicolare", oltre che nel significato di "diretto come il filo a piombo", da un paio di secoli in matematica si usa anche per indicare quando un segmento forma con un altro due angoli retti, come C' nella figura immediatamente a destra.

D è un quadrato, ossia una figura costituita da 4 segmenti uguali (chiamati lati) ciascuno con gli estremi in comune con due altri lati e che si incontrano formando 4 angoli retti.  E è un rettangolo, costituito da 4 segmenti che si incontrano come quelli del quadrato ma che non sono necessariamente uguali. Come nel caso del cerchio, si possono chiamare "quadrato" e "rettangolo" non solo i contorni ma anche le parti interne.

Nel linguaggio comune gli angoli (ad esempi gli angoli di un tavolo o di una stanza) sono degli spazi limitati. In matematica un angolo - vedi F - è uno spazio illimitato, descritto da una semiretta che parte da un punto, proseguendo in una certa direzione (vedi i "puntini"), che viene fatta ruotare in verso antiorario.  Il goniometro, G , misura la ampiezza di un angolo in gradi (un "grado" è una fettina di un cerchio suddiviso in 360 fettine uguali, o una fettina di metà di un cerchio diviso in 180 fettine). Un angolo retto misura 180/2 = 90 gradi. Invece di "gradi" di può usare il simbolo "°". L'angolo misurato nella figura misura 45°. Al posto di "goniometro" è usato anche il termine rapportatore.

H è un triangolo, figura costituita da 3 segmenti ciascuno con due estremi in comune gli altri.  K è un triangolo rettangolo, ossia un triangolo che ha un angolo retto (i lati corti si chiamano cateti, quello lungo ipotenusa).

L è un parallelogramma: ha i lati due a due uguali, come un rettangolo, ma gli angoli non è detto che siano retti. Il nome deriva dal fatto che i lati sono comunque (come nel caso del rettangolo) tra loro paralleli, ossia hanno la stessa inclinazione.  Nel caso particolare in cui i lati sono uguali, un parallelogramma viene chiamato rombo.  M è invece un trapezio; così sono chiamate le figure con 4 lati di cui almeno 2 paralleli (il trapezio degli acrobati è chiamato così perchè le due funi che sorreggono la barra sono parallele).

Le figure costituite da un numero qualunque di lati ciascuo dei quali con gli estremi in comune con altri due si chiamano poligoni. Triangoli e trapezi ne sono degli esempi. Un altro esempio è N. Gli estremi dei vari lati si chiamano vertici del poligono.

P rappresenta una retta; i "puntini" illustrano il fatto che la linea prosegue mantenendo la stessa inclinazione da entrambe le parti.

Q è un cubo. Hanno la forma di un cubo i dadi da gioco.  Un cubo può essere pensato come lo spazio descritto da un quadrato che si muove in direzione perpendicolare a sé stesso di un tratto pari alla lunghezza del lato.  I quadrati che racchiudono la figura ottenuta si chiamano facce del cubo. I lati delle facce sono chiamati lati del cubo.  R è un parallelepipedo rettangolo: è lo spazio descritto da un rettangolo che si muove in direzione perpendicolare a sé stesso per un certo tratto.  Queste figure si chiamano solide, a differenza dei poligoni e dei cerchi che si chiamano figure piane.

Sono figure solide anche le altre sopra illustrate (assieme alle loro ombre).  S è una sfera, ottenibile facendo ruotare un cerchio attorno ad un suo diametro (anche in questo caso posso considerare punti della sfera anche quelli al suo interno).  T è una piramide, ottenibile congiungendo i vertici di un poligono con un punto che non sta nello stesso piano del poligono.  U è un cilindro, ottenuto ruotando di 360° un rettangolo attorno ad un suo lato.  V è un cono, ottenuto ruotando un triangolo rettangolo attorno a un cateto.

  Ricordiamo, con delle animazioni  (tratte da questo sito),  alcune relazioni e proprietà.

    Come calcolare l'area dei triangoli

    Come calcolare l'area dei parallelogrammi

    La somma degli angoli di un triangolo quanto vale?

    Che cosa dice il teorema di Piatgora?

    Che cosa ottengo ruotando un triangolo rettangolo attorno ad un cateto?

    Quanto valgono il perimetro e l'area di un cerchio?

Sin dalla scuola di base occorre imparare, oltre a disegnare con carta, matita, riga, squadra e compasso, a fare semplici figure col computer, sia per rendersi conto di come sono realizzate le immagini digitali, sia per avviare alla messa a fuoco della natura "astratta" (ma "concretamente" utile) della matematica (i punti senza dimensione non posso tracciarli, le curve di spessore nullo non esistono, ... ma è comodo far finta che ...).  Per avviare a queste riflessioni può essere utile ricorrere ad un semplice programmino per disegnare, come quello che puoi trovare qui.     Successivamente potrai usare un programmino per disegnare su carta quadrettata.

Esercizi per la scuola di base