Equazioni differenziali - 2

  Alla voce  equazioni differenziali 1 abbiamo introdotti i primi esempi di equazioni differenziali.
    Facciamo qualche breve considerazione storica su di esse.
    Lo studio delle prime equazioni differenziali risale alla fine del XVII secolo, quando, da Newton e Leibniz, venne individuato il teorema fondamentale dell'analisi (vedi), che ha messo in relazione la derivazione e l'integrazione.  Emerse, presto, il problema che, a differenza della derivazione, per la quale esiste un procedimento standard per associare ad una funzione la sua funzione derivata, non c'è una tecnica standard per associare ad una funzione le sue antiderivate.  Si deve arrivare al XVIII secolo per la messa a punto di tecniche specifiche per la risoluzione di varie classi di equazioni differenziali e per la dimostrazione di alcuni teoremi che assicurano l'esistenza delle soluzioni di equazioni differenziali che soddisfano certe condizioni generali.  Di questi aspetti ti occuperari se proseguirai gli studi in ambito matematico o fisico.
    Qualche approfondimento sui modelli differenziali lo puoi trovare nei prossimi paragrafi, in cui faremo un esteso impiego di WolframAlpha, e, volendo, nella la scheda Modelli differenziali  (vedi qui le altre schede).

    Ricordiamo con un esempio come si può afforntare lo studio di una equazione differenziale del 1º ordine.

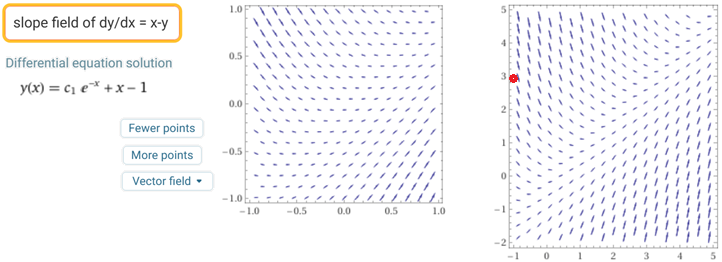
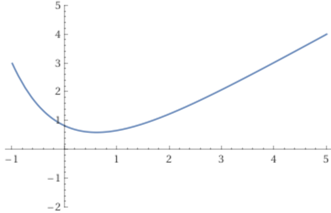
    L'immagine a destra è stata ottenuta con  slope field of dy/dx = x-y , for x=-1..5, y=-2..5  nel caso mi intersessi studiare alcune soluzioni particolari, che posso risolvere con comandi come il seguente, con cui traccio la soluzione il cui grafico passa per il punto (-1,3), segnato sopra in rosso:

plot y(x) = x + 5 e^(-x - 1) - 1, x=-1..5, y=-2..5

    Illistriamo con qualche esempio lo studio delle equazioni differenziali del 2º ordine.

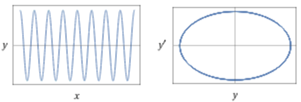
    Il primo esempio rappresenta l'equazione differenziale che esprime la posizione di un oggetto fissato ad una molla.  Se y è la distanza (in una opportuna unità di misura) e x il tempo (in una opportuna unità di misura), la relazione è del tipo  y"(x) = -k·y(x).  Se fisso, in un istante dato, la posizione e la velocità, posso esplicitare y in funzione di x. Nella figura è rappresentato oltre al grafico della soluzione (in un particolare caso) quello della relazione che lega y e la velocità y', che in questo caso è una curva chiusa in quanto la soluzione è periodica (riportiamo solo i grafici forniti dal comando seguente).

y"(x) = -4*y(x), y(0) = 2, y'(0) = 0

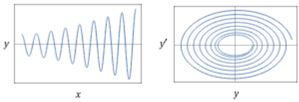
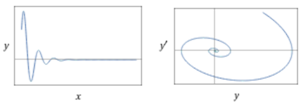
    Gli esempi successivi sono riferiti a situazioni simili alla precedente in cui però, nel primo caso, l'oggetto viene spinto ad ogni passaggio, aumentando l'ampiezza delle oscillazioni, e, nel secondo, si è in presenza di un fluido che smorza le oscillazioni.

y"(x) = -4*y(x)+cos(2*x), y(0) = 2, y'(0) = 0

y"(x) = -4*y(x)-y'(x), y(0) = 1, y'(0) = 3

    Le equazioni differenziali alle derivate parziali  (che coinvolgono le derivate parziali della funzione incognita rispetto a più di una variabile), a differenza di quelle ordinarie, hanno soluzioni che non dipendono da costanti arbitrarie ma da funzioni arbitrarie.  Sono usate soprattutto per affrontare alcuni argomenti di fisica.  Vediamo tre esempi nei quali l'incognita è f.

d/dy f(x,y) = x

    c1(x) indica una generica funzione di x. Ecco due esempi di soluzione:

d^2/dy^2 f(x,y) = x

 

d/dx d/dy f(x,y) = 0