Disequazioni

#1  Abbiamo considerato più volte disequazioni, ad esempio:
•  per descrivere figure
•  nelle attività di calcolo approssimato,
•  per restringere o definire i domini di equazioni che modellizzano certi problemi.

    Le disequazioni, ovviamente, possono essere utilizzate per modellizzare direttamente situazioni. Ad esempio, per riferirsi al contesto economico già considerato alla voce "proporzionalità inversa",
− indichiamo con Ct(n) il costo totale in euro della produzione, da parte di una piccola fabbrica, di n prodotti che abbiano ciascuno il costo incorporato (per materiali, energia consumata, …) di 50 €  nel caso in cui le spese fisse (per locali, dipendenti, …) siano di 30mila €, ossia che Ct(n) = 30000+50n,
− supponiamo che ogni prodotto sia venduto al prezzo di 150 €, così che il ricavo per la vendita di n prodotti sia Rt(n) = 150n.
− allora la la disequazione Ct ≤ Rt indica una attività produttiva non in perdita (il "?", nel grafico a lato, è il volume di produzione che segna il passaggio da una situazione di passivo a una di attivo).
    Determiniamo quando Ct ≤ Rt, ossia quanto vale "?".
30000+50n ≤ 150n  equivale a  300000 ≤ 100n  ossia a  300 ≤ n.

 

#2  Quando una disequazione contiene variabili ci si può porre il problema di risolverla rispetto a una variabile fissata (o a una coppia di variabili o …).

    Alcune "disequazioni", come 3 ≤ x < 7, ad essere rigorosi non sono delle vere e proprie disequazioni, ma sono dei sistemi di disequazioni:
3 ≤ x < 7   sta per
          3 ≤ x  AND  x < 7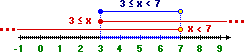		     

    Nel caso della risoluzione di disequazioni contenenti un'unica variabile in genere conviene combinare il metodo grafico (per capire come sono fatti gli intervalli costituiti dalle soluzioni) e il metodo algebrico (per trovare gli estremi di tali intervalli).
•  Nel caso della disequazione √(100-x2) > 6 dal grafico ricavo che ha come insieme di soluzioni un intervallo (–h, h). Risolvendo algebricamente l'equazione √(100-x2) = 6 ottengo che h vale 8:
  √(100-x2) = 6 → 100-x2 = 36 √ x2 = 64 → x = ±8 		  

#3  Per risolvere una disequazione si usano manipolazioni simboliche simili a quelle impiegate per risolvere equazioni:   "invertire la disequazione" (a<b → b>a, invertendo anche "<") e:
•  sostituire un membro della disequazione con un termine ad esso equivalente:
ciò richiede attenzioni simili a quelle richiamate per le equazioni (il dominio può cambiare);
•  applicare una funzione a entrambi i membri:
ciò richiede qualche attenzione in più rispetto a quelle viste per le equazioni, in particolare l'individuazione degli intervalli in cui tale funzione cresce/decresce; nel seguito approfondiamo questo aspetto.

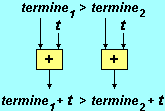
#4  Se addiziono o sottraggo lo stesso numero a due numeri A e B, ottengo due nuovi numeri A' e B' che sono nello stesso ordine che c'era tra A e B. Posso quindi applicare le trasformazioni schematizzate sotto (con l'attenzione ai cambiamenti di dominio che possono esserci se t contiene la variabile rispetto a cui risolviamo la disequazione):

     

    Vediamo ad es. come risolvere algebricamente la disequazione 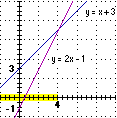x + 3 > 2x – 1:
x+3 > 2x–1  [applico "–x"] → 3 > x–1  [applico "+1"] → 4 > x
    È facile verificare graficamente che le soluzioni sono proprio queste (se "schizzo" i grafici di x → x+3 e di x → 2x–1 posso osservare che il primo sta sopra al secondo proprio per x<4).

  

#5  Due funzioni particolarmente importanti sono la negazione (o "cambio segno"), x → –x, e il passaggio al reciproco, x → 1/x, di cui a fianco sono riprodotti parzialmente i grafici:
 
–  la prima è decrescente in R,
 
–  la seconda, che è definita in (–∞,0)∪(0,∞), cioè in {x ∈ R : x ≠ 0}, è decrescente sia in (–∞,0) che in (0,∞).
 
Esempi d'uso:

 

•  Per risolvere –(x+1) > 3 posso applicare il "cambio-segno". Poiché si tratta di una funzione decrescente devo inverire l'ordine: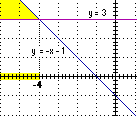
–(x+1)>3  [cambio segno] → x+1<–3  [applico "–1"] → x<–4
    Schizzando i grafici di x → –x–1 e di x → 3 si ottiene una conferma di queste soluzioni.

  

•  Risolviamo algebricamente 1/x > 2. Osservo che per x<0 1/x è negativo e quindi per tali valori la disequazione è sicuramente falsa. Allora mi restringo all'intervallo 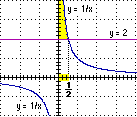(0,∞), cioè a x>0. Applico il "passaggio al reciproco" che in tale intervallo è decrescente. Ottengo: x<1/2. Ricordando la restrizione fatta, la disequazione equivale a: x<1/2 AND x>0, cioè a 0<x<1/2; le soluzioni sono, quindi, i numeri dell'intervallo (0,1/2). La cosa è verificabile osservando che il grafico di x → 1/x sta sopra a y=2 per 0<x<1/2.
Attenzione È un errore comune, di fronte a una disequazione come la precedente, pensare che x → 1/x sia ovunque decrescente e quindi trasformare l'eq. in x < 1/2 senza la condizione x>0.

  

#6  Sulla risoluzione delle disequazioni, così come su quella dell'equazioni, si ritornerà in successive sezioni. Ci limitiamo solo a ricordare i procedimenti schematizzati sotto:

     

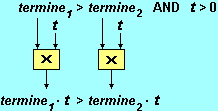
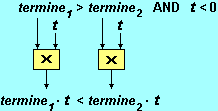
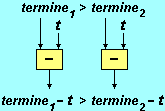
    se moltiplico per lo stesso numero positivo [negativo] due numeri A e B ottengo due nuovi numeri A' e B' che sono nello stesso ordine [nell'ordine opposto a quello] che c'era tra A e B.
    Moltiplicare per un numero negativo equivale a moltiplicare per un numero positivo e poi applicare un cambio segno: ciò spiega l'inversione della diseguaglianza. 
•  Consideriamo ad esempio la disequazione:   
x + 1   >   x − 2
——— ———
−5 − x2 −5 − x2
Poiché –5–x2 è negativo, può essere trasformata (usando tale termine come il t dello schema, e poi operando la semplificazione t/t → 1) in  x+1 < x–2, e poi (applicando "–x") in 1<–2, che è falsa: la disequazione non ha soluzioni.

#7  Abbiamo visto l'importanza di riferirsi a una rappresentazione grafica delle disequazioni (che, a seconda dei casi, può essere realizzata effettivamente, magari mediante un semplice schizzo, o solo visualizzata mentalmente). In questo ambito è spesso utile saper ottenere il grafico di una funzione mediante trasformazioni geometriche ( Funzione 2) a partire da una "banca" di grafici di funzioni di cui si dovrebbe conoscere l'andamento senza esitazioni:
x → ax+b, x → x2, x → √x, x → |x|, x → xn, x → k/x, e, più avanti: x → sin(x), x → cos(x), x → tan(x), x → ax, x → log(x), …
Consideriamo ad esempio:
  x + 1   <  2
———
x − 1
    Posso schizzare facilmente il grafico della funzione che ad x traccia il termine a sinistra, che so essere indefinito per x=1, riconducendomi a quello di y = 1/x in vari modi:
•  fare la divisone tra x+1 e x-1 ottenendo 1 con resto 2, da cui l'equivalenza del termine a sinistra con 1 + 2/(x-1) e la conclusione che il nostro grafico è l'iperbole y = 2/x traslata a destra di 1 e in alto di 1;
•  arrivare alla stessa conclusione con questa manipolazione:
riscrivere  x+1  come  x−1 + …,  ossia come  (x−1) + 2,  da cui, distribuendo la divisione:
(x+1)/(x−1) = (x−1)/(x−1) + 2/(x−1) = 1+2/(x−1)
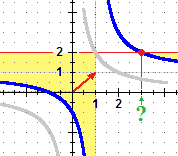    Dal confronto di questo grafico con la retta y=2 concludo che le soluzioni sono costituite dagli intervalli (-∞, 1) e (h, ∞) dove h è l'ascissa del punto di intersezione. 		 
    Trovo h risolvendo l'equazione 1+2/(x-1) = 2:
2/(x-1) = 1  →  2 = x-1  →  2+1 = x  →  x = 3.
    Quindi le soluzioni formano l'insieme (-∞, 1) U (3, ∞).

 

Esercizi:       testo1 e soluz.,   testo2 e soluz.,   testo3 e soluz.,   testo4 e soluz.,
testo5 e soluz.,   testo6 e soluz.,   testo7 e soluz.,   testo8 e soluz.
 

Altri esercizi per la scuola di base