Un programma in JavaScript (vedi qui per approfondimenti) Facciamo ricorso ad uno dei molti siti in cui si possono provare ad eseguire degli script:  www.learnhindituts.com/online-javascript-compiler. Introducendo questo programma, di cui è facile capire il significato  ("Math." deve precedere il nome di operazioni matematiche più complesse, come sqrt - radice quadrata, pow - elevamento a potenza, round - arrotondamento, ...(vedi);  il comando Html <br> - break - indica "a capo"):

function F(x) { return Math.sqrt(1-x*x) }
x = -0.8
n=1; L0 = 0
for(k=1; k<14; k=k+1) {
  dx = (1-x)/n; L = 0; x1 = 1;
  for(i=1;i<=n;i=i+1) {x2=1-dx*i; dy=F(x2)-F(x1); dP=Math.sqrt(dx*dx+dy*dy); L=L+dP; x1=x2}
  dL=L-L0; L0=L; document.write("n = ", n, " _ L = ", L," _ dL = ", dL, "<br>"); n=n*4 }

Si ottiene:

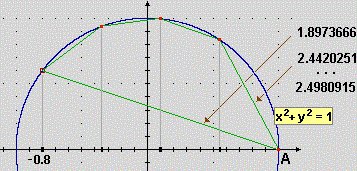
n = 1 _ L = 1.8973665961010275 _ dL = 1.8973665961010275
n = 4 _ L = 2.4420250892037814 _ dL = 0.5446584931027538
n = 16 _ L = 2.491823296986896 _ dL = 0.04979820778311472
n = 64 _ L = 2.4973536528292777 _ dL = 0.005530355842381596
n = 256 _ L = 2.498002111315031 _ dL = 0.0006484584857533449
n = 1024 _ L = 2.498080539032036 _ dL = 0.00007842771700516948
n = 4096 _ L = 2.4980901798595996 _ dL = 0.000009640827563384136
n = 16384 _ L = 2.4980913748516547 _ dL = 0.0000011949920550868853
n = 65536 _ L = 2.498091523595359 _ dL = 1.4874370446449348e-7
n = 262144 _ L = 2.498091542149023 _ dL = 1.8553663938547515e-8
n = 1048576 _ L = 2.498091544465893 _ dL = 2.3168698071174276e-9
n = 4194304 _ L = 2.4980915447549426 _ dL = 2.8904967308562846e-10
n = 16777216 _ L = 2.4980915447914733 _ dL = 3.653077840226615e-11

Con x = -1:

n = 1 _ L = 2 _ dL = 2
n = 4 _ L = 3.035276180410083 _ dL = 1.035276180410083
n = 16 _ L = 3.1285443165443008 _ dL = 0.0932681361342178
n = 64 _ L = 3.1399669432921904 _ dL = 0.01142262674788963
n = 256 _ L = 3.141389590749035 _ dL = 0.0014226474568443948
n = 1024 _ L = 3.1415672753316537 _ dL = 0.00017768458261890885
n = 4096 _ L = 3.1415894814502505 _ dL = 0.000022206118596823643
n = 16384 _ L = 3.1415922570768133 _ dL = 0.0000027756265628120502
n = 65536 _ L = 3.1415926040257864 _ dL = 3.469489731067199e-7
n = 262144 _ L = 3.141592647394258 _ dL = 4.336847148067591e-8
n = 1048576 _ L = 3.14159265281532 _ dL = 5.421062265753562e-9
n = 4194304 _ L = 3.141592653492851 _ dL = 6.775309202566859e-10
n = 16777216 _ L = 3.1415926535778027 _ dL = 8.495160130905788e-11

Da queste uscite possiamo osservare che, man mano che quadruplico il numero dei tratti, i valori aumentano di una quantità man mano circa 10 volte più piccola.  Per x = -0.8 posso prendere 2.498091544796;  per x = -1 posso prendere 3.14159265359.