Diagrammi

  (1)-(6) sono sei diversi diagrammi che rappresentano la ripartizione di un certo totale nelle sue parti A, B e C, in alternativa alla rappresentazione percentuale, riportata nella tabella a sinistra.

A B C totale  %  15.5 47.8 36.7 100

(1)

^{(2)     (3)
(4)   (5)   (6)}

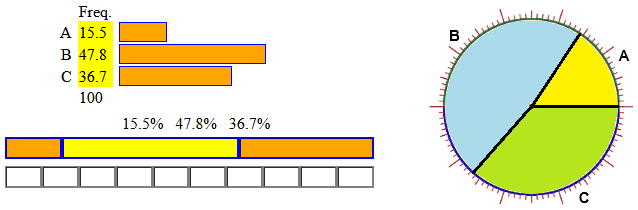
(1) è un diagramma a striscia; (2)-(4) sono istogrammi, (5) e (6) sono diagrammi a settori circolari (o a torta). In ogni caso viene rappresentato un insieme di valori numerici mediante una grandezza geometrica: lunghezza (di un segmento, un rettangolo o un parallelepipedo) o ampiezza angolare (di un settore di cerchio o di cilindro).  (2)-(4) sono chiamati anche diagrammi a barre, per specificare che quel che conta per confrontare i dati è l'altezza delle "barre"; un uso più specifico degli istogrammi è discusso alla voce distribuzione.

(1), (2) e (5) vengono chiamati anche areogrammi in quanto i valori numerici rappresentati sono proporzionali non solo alle lunghezze dei rettangoli o alle ampiezze dei settori circolari, ma anche alle loro aree. Analogamente (4) e (6) vengono chiamati anche stereogrammi (dal greco stereós, che significa solido) in quanto i valori numerici sono proporzionali anche ai volumi dei parallelepipedi o delle fette di cilindro raffigurate.

Gli istogrammi facilitano il confronto tra i vari dati, i diagrammi a striscia facilitano il confronto tra i singoli dati e il loro totale, gli areogrammi combinano i vantaggi dei due precedenti tipi di diagrammi, ma con essi è più difficile risalire ai valori numerici (gli istogrammi in genere sono dotati di un segmento graduato che permette di associare lunghezze e valori numerici).  La rappresentazione (6) forse è la più "carina", ma è anche la peggiore:  nella inclinazione della torta gli angoli vengono deformati (gli angoli che in un diagramma piatto - 5 - sono vicini al diametro orizzontale/verticale nel diagramma inclinato - 6 - appaiono ingranditi/rimpiccioliti e ciò rende più difficile il confronto quantitativo). Esistono anche stereogrammi che usano sfere invece che cilindri: sono "carini" ma è assurdo impiegarli per dare delle informazioni statistiche (ricerche di psicologia hanno messo in luce che l'uomo riesce a valutare facilmente rapporti tra segmenti, meno facilmente tra angoli e molto difficilmente tra volumi di sfere).

• Le rappresentazioni grafiche presentate sopra possono essere realizzate con programmini online presenti qui. Ecco ad esempio che cosa si può ottenere usando "istogramma a barre", "istogramma a striscia", "areogramma" e "areogrammi":

Per rappresentare insiemi di valori numerici si usano anche gli ideogrammi, che impiegano figure simboliche (idee) in quantità (ideogramma a sinistra) o in estensione (ideogramma a destra) proporzionale ai dati.

Nel secondo caso è frequente trovare rappresentazioni scorrette: ad es. per il confronto del consumo di vino per abitante di 90 litri con quello di 60 litri si può trovare il disegno di una bottiglia alta 1.5 volte la bottiglia che rappresenta i 60 litri (90/60 = 1.5) invece del disegno di una bottiglia che abbia volume pari a 1.5 volte quello dell'altra bottiglia. Gli ideogrammi-stereogrammi come quello sopra a destra (che, se fatti bene, rappresentano dati mediante il volume di oggetti tridimensionali di uguale forma) sono tipicamente impiegati per confrontare dati con ordini di grandezza molto diversi.       Ad es. i due cubi a destra possono rappresentare due dati di cui uno è circa 1/1000 dell'altro (infatti il cubo piccolo ha lato pari circa a 1/10 di quello del cubo grosso, per cui sta circa 10·10·10 volte in esso), confronto che sarebbe meno efficacemente realizzabile usando rappresentazioni lineari (un segmento lungo 1/1000 dell'altro) o areogrammi (un quadrato con lato 1/32 quello dell'altro: 32·32 fa circa 1000). Tutto ciò rientra più in generale nel fatto che se trasformo con fattore di scala K le dimensioni di un oggetto [ad es. K=3, come nella figura a sinistra], il fattore di scala della superficie è K·K [3² = 9] e il fattore di scala del volume è K·K·K [3³ = 27]. Come abbiamo già osservato le rappresentazioni tridimensionali, pur consentendo efficaci confronti quantitativi (maggiore, minore), non permettono di valutare facilmente i rapporti: nel caso raffigurato sopra a destra è intuitivo capire che il cubetto è molto più piccolo del cubo ma non è niente affatto immediato percepire che è un millesimo di esso.

Al posto di diagramma si può parlare di rappresentazione grafica o di grafico. Il termine grafico è però più spesso usato per indicare la rappresentazione di una relazione che intercorre tra i valori numerici di due grandezze, ad esempio tra le distanze d su una cartina in scala 1:5000 e le corrispondenti distanze D nella realtà (vedi il grafico tracciato a destra, su cui torniamo nel prossimo paragrafo).   Le grandezze sono rappresentate su due assi di riferimento, cioè due rette non parallele (in genere perpendicolari) ai cui punti sono stati associati i valori delle grandezze mediante opportune scale numeriche ( proporzionalità).  Se vogliamo rappresentare le due grandezze considerate nel paragrafo precedente:

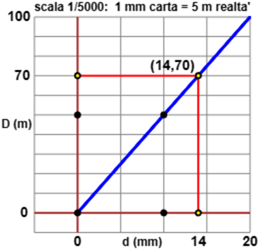–  fissiamo un punto a cui associamo i valori d = 0 e D = 0 [vedi la prima figura],
–  tracciati i due assi passanti per tale punto, pensiamo una coppia di valori (d,D) fino a cui vorremmo tracciare il grafico, ad esempio (14,70) [vedi la seconda figura]
–  consideriamo due valori (d,D) da segnare sui due assi vicini a 14 e 70 ma più "comodi", come 10 e 50 [vedi la terza figura],
–  a questo tracciamo la semiretta che parte da (0,0) e passa per (10,50) e segnamo sull'asse orizzontale una sequenza di punti a distanze uguali tra loro contenente 10 ed una sull'altro asse contenente 50 e (se non stiamo usando della carta quadrettata) traccimo una griglia di rette parallele ai due assi passante per tali punti [come si vede nella quarta figura],
–  infine posso evidenziare il punto (14,70), come nella figura tracciata nel paragrafo precedente.

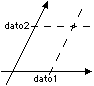
Volendo si possono indicare con delle frecce i versi secondo i quali i numeri segnati sui due assi crescono:  vedi la figura a destra.     I valori dato1 e dato2 vengono detti coordinate del punto tracciato nella figura, che, come abbiamo visto, viene designato anche con  (dato1, dato2);  dato1 e dato2 vengono detti, rispettivamente, ascissa e ordinata del punto. Nota.  Non è detto che un asse intersechi l'altro in corrispondenza del valore 0. Alcuni esempi sono raffigurati più avanti.

Nei casi in cui si ottengono punti isolati, per facilitare la lettura del grafico, invece dei soli punti si possono tracciare dei segmenti verticali o dei segmenti che congiungono un punto all'altro.

Nel caso in cui la relazione che intercorre tra le due grandezze numeriche sia espressa mediante una formula, quando si sa che tipo di grafico si deve ottenere (ad es. se si tratta di una relazione di proporzionalità, che ha come grafico una retta: ) può essere sufficiente individuare alcuni punti per poi tracciare senza altri calcoli l'intero grafico. In altri casi è necessario individuare via via più punti, fino, se ci si riesce, a capire l'andamento del grafico e a completarlo con linee che congiungono opportunamente i punti tracciati.     Ad es. nel caso di y = x2, se non sapessi che forma ha la rappresentazione grafica della relazione che intercorre tra x e y, e volessi tracciarla per i valori di x compresi tra -1 e 2, potrei calcolare il valore di y per x=-1, x=0, x=1, x=2 (come nella tabella sotto a destra) e rappresentare questi punti; congiungendoli con delle linee avrei una prima idea del grafico. Potrei poi infittire questa tabulazione, suddividendo l'intervallo [-1, 2] in un numero doppio di sottointervalli, ossia calcolando il valore di y anche per x=-0.5, x=0.5, … e ottenere la rappresentazione sotto al centro; ed eventualmente proseguire con una tabulazione più fitta …  [nei grafici seguenti "Dx" indica la distanza tra le linee verticali della griglia] x y -1 1 0 0 1 1 2 4

La scelta di scale opportune è importante al fine di rendere più leggibile il grafico o più evidente il fenomeno rappresentato. Occorre comunque tener conto della scala scelta per interpretare l'andamento del grafico: i due grafici a fianco rappresentano la stessa tabella di dati ma suggeriscono valutazioni diverse sull'evoluzione del fenomeno (l'andamento della disoccupazione in Italia in certi anni).

Altri tipi di diagrammi sono:
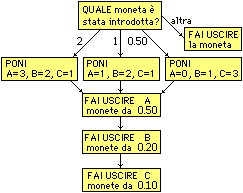
• i diagrammi di flusso, impiegati per descrivere procedimenti di calcolo o la logica di funzionamento di macchine, e • i grafi per rappresentare trasferimenti di oggetti, di energia, …, relazioni di causa-effetto [ esempio], struttura dei termini [ grafi], …
• i cosiddetti diagrammi di (Eulero-)Venn (usati per primo, probabilmente, da Eulero, nel XVIII sec., e diffusi da Venn, nel XIX sec.): nell'esempio a fianco i multipli di 2 e di 5 sono rappresentati dai punti di due figure ovali; i punti comuni alle due figure rappresentano i multipli sia di 2 che di 5; il diagramma viene usato per evidenziare che i multipli di 2 e di 5 sono i multipli di 10. [qualche altro esempio d'uso:  numeri,  figure(2),  dipendenza e indipendenza]

    Per altre riflessioni sulle rappresentazioni grafiche discusse in questi ultimi punti, altre rappresentazioni ad esse simili e considerazioni sulle ambiguità dei diagrammi di Venn clicca QUI.
    Un tipo di notazione grafica impiegato frequentemente per rappresentare informazioni statistiche è illustrato nel seguente esercizio: testo e soluzione. Queste rappresentazioni vengono etichettate con vari nomi: cartogrammi, mappe tematiche, mappe coropletiche, ….

  Perchè si usano le rappresentazioni grafiche?
Un primo aspetto, evidente, è che per la nostra mente è più facile e immediato confrontare due quantità descritte in forma geometrica (come lunghezze, aree, …) piuttosto che in forma numerica.  Un altro aspetto è che spesso mediante una rappresentazione grafica si possono sintetizzare molte informazioni diverse e si riesce in modo più agevole a sviluppare dei ragionamenti sul complesso di esse. Su questo aspetto si ritorna in molte altre voci degli Oggetti Matematici. Facciamo un piccolo esempio per illustrarlo.

Voglio realizzare un recinto rettangolare per animali ampio 12 m2 con la parte frontale in pietra e gli altri lati in legno.  La recinzione in pietra costa 40 € al metro, quella in legno 16 € al metro. Come devo scegliere la forma del recinto per spendere il meno possibile? Posso procedere per tentativi. Se prendo il lato frontale di 1 m quelli di fianco devono essere di 12 m, in modo che l'area sia di 12 m2 (1·12 = 12);  il costo diventa di 40 € per la parte in pietra e di (12+12+1)·16 € per quella in legno;  in tutto 440 €.  Se prendo il lato frontale di 3 m quelli di fianco devono essere di 4 m (3·4 = 12);  il costo diventa di 120 € per la parte in pietra e di (4+4+3)·16 € per quella in legno;  in tutto 296 €.  Posso procedere con altre prove.  Ma se riporto le informazioni via via elaborate su un grafico, indicando sull'asse orizzontale la larghezza della parte frontale e sull'asse verticale il corrispondente costo, capisco meglio come cambia la spesa al variare della forma del recinto e deduco che facendo il lato frontale ampio 2 metri e mezzo circa riesco a contenere i costi.  Aiutandomi col grafico posso indirizzare ulteriori tentativi per precisare meglio la valutazione. E riportando gli esiti dei calcoli sul grafico posso anche accorgermi di eventuali errori di calcolo:  otterrei punti collocati in posizioni "strane" rispetto agli altri e capirei di aver commesso qualche sbaglio.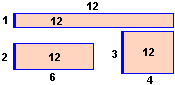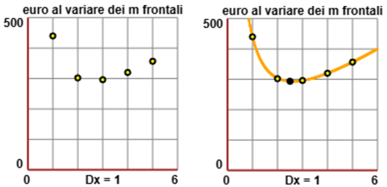

Esercizi:    testo  e  soluzione,    testo  e  soluzione,    testo  e  soluzione,    testo  e  soluzione
 

Altri esercizi per la scuola di base