Assiomi e loro modelli

  Il riferimento ai contesti (e un altro uso della parola "modello")

La parola  modello in matematica, oltre che per indicare:
– una "rappresentazione matematica" di un fenomeno, una situazione, un oggetto, … riferito a un certo contesto,
    viene usata anche, in un modo quasi opposto, per indicare
– una "interpretazione" in qualche contesto matematico di un insieme di proprietà.
    Il primo significato corrisponde al significato 5 nella voce di un dizionario della lingua italiana riportata in appendice, ed è vicino, ad es., ai significati 4 e 9 (è qualcosa di più "semplice" rispetto alla "realtà" che rappresenta).  Il secondo significato corrisponde al significato 13, ed è vicino a significati 1 e 7 (è qualcosa di più "complesso" rispetto alla "idea" che rappresenta).  Facciamo due esempi:

•  da una parte si può dire che il concetto di gruppo è un modello matematico per diverse strutture:  numeri rispetto all'addizione,  le traslazioni rispetto alla composizione, …,
  dall'altra si dice anche che queste strutture sono un modello degli assiomi di gruppo, nel senso che queste proprietà (ad es.: per ogni x esiste x' tale che  x x'  sia l'elemento neutro, …) sono vere se interpretate in queste strutture (ogni numero è dotato di un opposto, per ogni traslazione c'è la sua inversa, …);  non costituiscono, invece, un modello degli assiomi di gruppo i numeri interi rispetto alla moltiplicazione (l'elemento neutro è 1, ma dato x intero diverso da 1 e da -1 non esiste alcun y intero tale che x·y =1);

•  da una parte si può dire che il concetto di relazione d'ordine è un modello matematico per:   il "≤" tra numeri interi o tra numeri reali,  il "⊂" tra insiemi,  l'ordinamento alfabetico tra parole,  la relazione "m è divisibile per n" tra numeri interi positivi (da "160 è divisibile per 16" e "16 è divisibile per 8" deduco che "160 è divisibile per 8"),  la "X è un antenato di Y" tra essere umani, …,
  dall'altra si dice anche che tali insiemi (considerati rispetto a "≤", "⊂", …) sono un modello degli assiomi di relazione d'ordine;  non costituiscono, invece, un modello di tali assiomi l'insieme degli esseri umani rispetto alla relazione "essere genitore di" (dai fatti che X sia genitore di Y e Y di Z non posso dedurre che X sia genitore di Z).

  Facciamo qualche esempio di questo nuovo significato di "modello" (sviluppatosi a cavallo del XIX e XX secolo) riferendoci alla geometria (una prima rigorosa presentazione assiomatica della geometria - o, come vedremo ora, delle geometrie - è dovuta ad Hilbert, nel 1899).
    Consideriamo le seguenti tre proprietà riferite a una struttura matematica in cui siano presenti due tipi di oggetti, che chiameremo punti e rette, e una relazione Per(r,P) tra rette e punti che, intuitivamente, possiamo pensare come: la retta r passa per il punto P, ovvero: il punto P sta sulla retta r. Indichiamo i punti con variabili maiuscole e le rette con variabili minuscole.

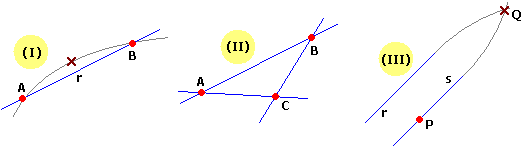
(I)    Per due punti passa una e una sola retta
(II)   Esistono almeno tre punti che non stanno sulla stessa retta
(III)  Se P non sta su r esiste una e una sola retta s passante per P senza punti in comune con r.

Abbiamo scritto le proprietà a parole; avremmo dovuto, ad essere rigorosi, usare il simbolo Per e scrivere, ad esempio al posto di (I): se A ≠ B esiste una sola r tale che Per(r,A) e Per(r,B).

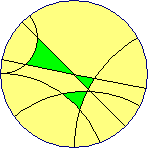
Ovviamente il piano euclideo verifica queste proprietà, ovvero è un modello di questi tre assiomi.  Infatti (vedi figura seguente):  (I) presi A e B distinti vi è sola retta r = AB che passa per essi;  (II) esistono triangoli;  (III) data r non passante per P posso prendere come s la retta di eguale inclinazione passante per P: non esiste nessun punto Q che sta sulle due rette, ovvero nessuna soluzione (x,y) del sistema formato dalle equazioni in x e y che descrivono le due rette.

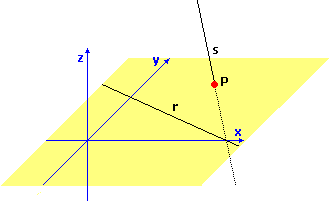Lo spazio euclideo tridimensionale invece non soddisfa (III). Si prendano, ad es., r e P sul piano xy:  una qualunque retta s passante per P che non stia su tale piano non ha alcun punto in comune con r.

Dalle proprietà (I), (II) e (III) si può dimostrare che esistono infiniti punti e infinite rette?     Il concetto di "modello" è utile per affrontare quesiti come questo. Infatti se troviamo uno "spazio" che verifica tali proprietà e ha un numero finito di punti e di rette possiamo concludere che l'esistenza di infiniti punti e rette non è una conseguenza di (I), (II) e (III): altrimenti non potrebbe esistere un contesto in cui non si verifica essa mentre queste si verificano.

Ecco l'esempio; è lo spazio formato dai quattro paesi (o "punti") A, B, C e D e dalle strade (o "rette") r1, r2, …, r6 che li congiungono raffigurato qui a lato: (I) ogni coppia di paesi è congiunta da una sola strada, (II) C non sta sulla strada AB, (III) data una strada che congiunge due paesi quella che congiunge gli altri due non ha punti in comune con essa. Non esiste, invece, alcuno spazio a 3 punti che, verificate la (I) e la (II), verifichi anche la (III): vedi la figura all'estrema destra (tutte e tre le "rette" hanno punti in comune).

Vediamo qualche spazio più significativo in cui non vale (III) mentre valgono (I) e (II). Consideriamo lo spazio (già considerato qui) i cui "punti" stanno sulla superficie di una sfera e le cui "rette" sono le rotte rettilinee, ossia i cerchi massimi sulla sfera, i cerchi che hanno lo stesso raggio della sfera: sono le linee lungo cui muoversi per andare da un punto ad un altro percorrendo la minor strada possibile.     Dato un punto A sulla sfera posso individuare un cerchio massimo scegliendo un qualunque altro punto; se scelgo H (vedi figura) lo stesso cerchio lo potrei individuare scegliendo K, il suo antipode (ossia il punto simmetrico ad H rispetto al centro); H e K sono equivalenti da questo punto di vista; inoltre per H e K, a differenza di quanto accade per A e B, non passa un solo cerchio massimo, ma infiniti (in figura ne sono tracciati due). Considero, quindi, due punti uno antipode dell'altro uguali come punti del nostro spazio.

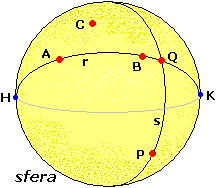
    A questo punto vale (I) (per due punti passa una sola rotta rettilinea, in quanto ciò non accade solo se i punti sono antipodi, ossia "lo stesso punto"). Ovviamente vale (II): vedi i punti A, B e C.
    Non vale (III): data r e fissato P non su di essa, qualunque s passante per P interseca r in un punto (il punto Q sulla figura).  Potremmo dire che non esiste alcuna parallela ad r passante per P (vedi).

Un altro esempio di spazio in cui non vale (III) mentre valgono (I) e (II):  lo spazio i cui "punti" stanno all'interno di un disco e le cui "rette" sono archi di cerchio che partono e arrivano sul bordo del disco formando angoli retti, o sono diametri (sono le infinite "rette" che passano per il centro del disco).     Vale (I): fissati A e B considero una corda r che passa per essi e pian piano la incurvo ("tirandola" verso il centro e costringendola a mantenere forma circolare): i due angoli, uguali, che forma con il bordo del disco man mano aumentano fino a che diventano retti; in questo modo ottengo la "retta" che passa per A e B. Vale, evidentemente, anche (II): dati A e B vi sono infiniti punti C che non stanno sulla "retta" AB.     Non vale (III): data r e fissato P non su di essa, vi sono infinite rette s passanti per P senza punti in comune con r.  Potremmo dire che esistono infinite parallele ad r passanti per P (vedi).

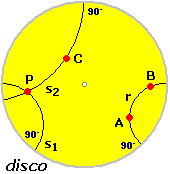
Entrambi questi spazi potremmo dotarli di concetti di distanza, direzione, angolo con molte proprietà in comune con il piano euclideo, ma avremmo anche varie proprietà che questo ha e che non sono verificate da essi. Ad esempio per il primo spazio avremmo ( vedi) che la somma degli angoli dei triangoli è maggiore di 180°, per il secondo avremmo (vedi figura a sinistra) che è minore di 180°. Lo studio di questi spazi rientra nella cosidetta area della matematica delle geometrie non euclidee.     Nei fenomeni fisici su scala astronomica le relazioni che intercorrono tra spazio, tempo, massa sono diverse da quelle che intuiamo nei fenomeni quotidiani.  Fu A. Einstein, nella sua Teoria della Relativit Generale, nel 1915, a mettere a punto il fatto che noi viviamo in un universo la cui geometria influenzata dalla forza di gravit delle stelle e delle galassie.

Ad esempio se intendiamo la retta come un modello della traiettoria dei raggi di luce, occorre tener conto che, in tali ambiti, la traiettoria della luce è influenzata dalla massa dei corpi celesti e, quindi, un andamento "rettilineo" non corrisponde più a quello che intuiamo vedendo i raggi di luce che filtrano da una superficie forata o proiettati da un faro. Un fascio di luce che inizialmente si propagasse lungo una striscia piatta potrebbe subire ora qua ora là delle deformazioni (affossamenti o protuberanze). Per studiare tali fenomeni si impiegano modelli matematici dello spazio fisico in cui i concetti di piano e di retta sono più vicini a quelli considerati in questi esempi che a quelli del piano euclideo. Potremmo interpretare i "piani" di queste geometrie come delle superfici che in certe zone si comportano in modo simile a delle sfere (in cui la somma degli angoli dei triangoli supera 180°), in altre zone si comportano come la superficie a destra (in cui vi sono triangoli con somma degli angoli minore di 180°).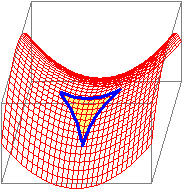

  Analogamente, vi possono essere dei "piani" in cui non vale il  teorema di Pitagora :  in alcuni casi si può trovare un triangolo in cui due lati a e b formano un angolo di 90° e il terzo lato c è superiore a √(a²+b²),  in altri se ne può trovare uno in cui due lati a e b formano un angolo di 90° e il terzo lato c è inferiore a √(a²+b²).
 

  Appendice

Ecco che cosa si può trovare in un vocabolario per la voce modello:

modèllo, sm. 1 Cosa o persona posta innanzi a un artista, per essere ritratta. 2 Bozzetto, abbozzo che precede la realizzazione definitiva di una costruzione o un'opera artistica. 3 Riproduzione in scala ridotta. 4 Prototipo o rappresentazione materiale di una macchina, un sistema, un fenomeno, … realizzato per fare sperimentazioni su di esso o studiarne proprietà. 5 Rappresentazione schematica di un fenomeno, un sistema, … usata per rappresentarne le caratteristiche principali e facilitarne lo studio (modello economico, modello matematico). 6 Abito confezionato su disegno originale. 7 Esempio da imitare (è un modello di onestà; è una fattoria modello - qui usato in funzione di aggettivo). 8 Esemplare originario e ideale. Archetipo. 9 Foglio di carta che riproduce le linee di un abito usato come guida per il taglio del tessuto. Più in generale, foglio che indica come realizzare un certo oggetto. 10 Forma (in legno o altro opportuno materiale) usata per ricavare lo stampo che accoglierà il metallo fuso. 11 Modulo tipo per pratiche burocratiche. 12 Persona che per mestiere posa per artisti o indossa capi o accessori di abbigliamento in sfilate di moda. 13 In Logica Matematica, un modello di una teoria descritta mediante un sistema di assiomi è un struttura matematica che li verifica (le strutture additive dei numeri reali e dei vettori sono entrambe un modello della teoria dei gruppi).