Interpolazione e approssimazioneCome si può cercare di approssimare un grafico sperimentale (il grafico della relazione tra due grandezze, un istogramma di distribuzione frutto di un rilevamento statistico, ...) con una curva "bella" (cioè che si può descrivere facilmente mediante funzioni elementari)?
Innanzi tutto facciamo qualche chiarimento terminologico, a partire da un esempio.
Interpolazione e approssimazione
| Supponiamo di avere le 5 informazioni descritte qui a destra e rappresentate sotto nella figura a sinistra relativamente a come un fenomeno y varia in funzione del fenomeno x. Per stimare i valori assunti da y per i valori di x intermedi possiamo approssimare l'intero fenomeno congiungendo i punti con segmenti (figura B). Questa tecnica si chiama interpolazione lineare: si ottiene una funzione (continua lineare a tratti) che nei 5 punti noti coincide con la nostra y in funzione di x; la possiamo usare per approssimare y per gli altri valori di x. Volendo ottenere una curva "totalmente liscia" (continua con tutte le sue derivate) potremmo individuare la funzione polinomiale di grado minimo che passa per tutti i 5 punti (figura C); ma questa interpolazione polinomiale in genere dà luogo a cattive approssimazioni. Un'ulteriore possibilità è approssimare l'andamento tra i vari dati rilevati con diverse funzioni polinomiali tali da garantire che la curva risultante sia abbastanza liscia (interpolazione con spline): ad esempio con funzioni polinomiali di 3° grado, imponendo che essa sia derivabile fino al 2° ordine, e che le derivate seconde nel primo e nell'ultimo punto siano nulle (figura D). | x y 2 5 3 20 4 28 5 20 7 20 |
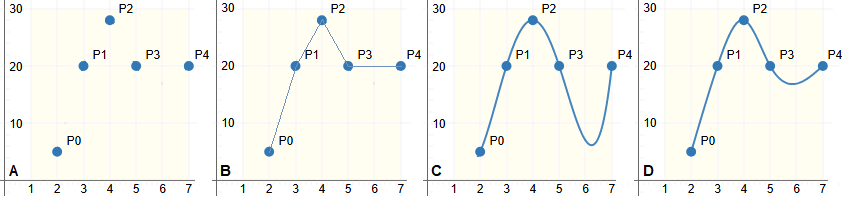
Per ottenere facilmente interpolazioni polinomiali e con spline puoi utilizzare i programmi presenti nel sito tools.timodenk.com.
Esercizio 1 (soluzione) Esercizio 2 (soluzione) Esercizio 3 (soluzione)
Non si parla, invece, di interpolazione, ma solo di approssimazione, se si vuole trovare una funzione il cui grafico passi vicino ai vari punti noti, senza necessariamente passare per essi. Questo è ciò che si farebbe se si volessero individuare delle regolarità nel fenomeno e si cercasse di descriverlo in modo sintetico, o se (ma non è questo il caso) si trattasse di rilevamenti ad alta sensibilità, soggetti a errori casuali non stimabili a priori, per cui non avrebbe senso porsi il problema di trovare curve che passino esattamente per i punti sperimentali.
Si parla di estrapolazione quando si cerca di prolungare un'interpolazione a sinistra (oltre il primo dato) o a destra (oltre l'ultimo).
In inglese si parla di curve fitting per indicare la costuzione di una curva che approssimi o interpoli dei punti sperimentali (la curva che abbia "the best fit", il migliore adattamento, secondo i criteri stabiliti).
Noi ci occuperemo in particolare di alcune tecniche generali di approssimazione.
Uso di scale semilogaritmiche, bilogaritmiche, quadratiche e cubiche
Nel file bilog.htm
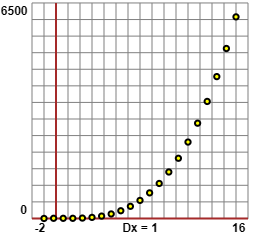
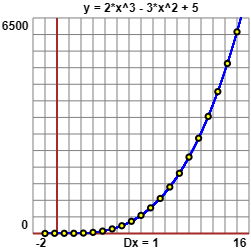
sono contenute delle coppie (x,y) ottenute tabulando una funzione polinomiale, sotto a sinistra rappresentate graficamente.
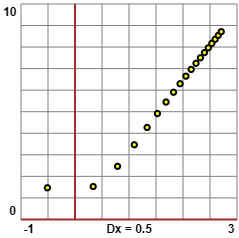
Per capire di quale grado è il polinomio possiamo trasformare i dati applicando il logaritmo sia alle x che alle y e rappresentare i nuovi dati (trasformati in "scala bilogartitmica"), come nella figura al centro,
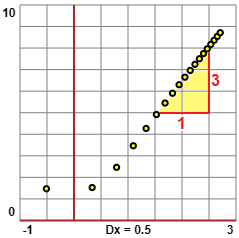
e osservare che tendono a disporsi lungo una retta, di cui (figura a destra) possiamo ricavare la pendenza (3).
QUI e QUI gli script con cui sono stati realizzati i due grafici.
|
Perché i nuovi dati tendono a disporsi lungo una retta? y = axn+bxn–1+… per x → ∞ tende a comportarsi come y = axn, che è trasformata in Qui puoi vedere come realizzare tutto ciò "a scatola nera" con lo script "regressione cubica". |
 |
Il metodo precedente ha successo se i dati hanno andamento polinomiale. Se supponiamo che i dati abbiano andamento
esponenziale, come quelli nel file semilog.htm, rappresentato graficamente sotto
a sinistra, possiamo trasformarli in "scala semilogaritmica", cioè applicando il logartitmo solo alle y.
Infatti una curva esponenziale così trasformata diventa una retta:
y = a eb x → Y =
Ecco, a destra, la trasformazione del grafico precedente ottenuta in tal modo. Cerchiamo di trovare a e b.
È stata tracciata una retta approssimante. Essa ha equazione
Qui puoi vedere come realizzare tutto ciò "a scatola nera" con lo script "regressione esponenziale".
Medie Mobili
Una tecnica molto impiegata per approssimare dati è costituita dall'uso delle medie mobili (di ordine 3), in particolare per analizzare serie storiche. Essa consiste nel sostituire ogni punto con quello avente comme coordinate le medie delle coordinate sue e dei punti ad esso precedente e seguente (il punto inziale e quello finale non vengono modificati, o vengono eliminati nella nuova rappresentazione). Ecco l'impiego di questa tecnica per analizzare i dati relativi a quasi un decennio di piogge a Genova e, in particolare, per individuare i fattori stagionali:
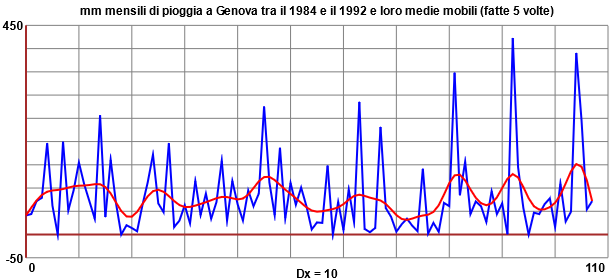
Qui puoi calcolare le medie mobili con lo script "medie mobili" (clicca "examples" per i dati relativi alle piogge a Genova).
Differenze successive
Supponiamo di dover analizzare i dati (1,2.25), (2,19.3), (3,65.2), (4,149), (5,302), (6,515), (7,820). Per capire come si evolvono posso ricorrere al calcolo delle differenze successive, che posso realizzare
facilmente impiegando lo script "differenze" presente qui. Ottengo:
2.25, 19.3, 65.2, 149, 302, 515, 820 i dati
17.05, 45.9, 83.8, 153, 213, 305 le differenze prime
28.85, 37.9, 69.2, 60,92 le differenze seconde
9.05, 31.3 ,-9.2, 32 le differenze terze
Tenendo conto che i dati non sono esatti e che gli errori di approssimazione facendo le sottrazioni aumentano (ad es. se su 149, 302, 515 e 820 l'errore fosse 5, sulle differenze prime sarebbe 10 e sulle terze sarebbe 20), posso ritenere che le differenze terze siano in crescita e che le quarte si siano stabilizzate. Ne deduco la approssimabilità con un polinomio di 3º grado.
Il metodo dei rapporti
Nel caso in cui si sia in grado di calcolare i valori di una funzione e si voglia capirne l'andamento, si può ricorre alla tecnica dei rapporti: se
19.3/2.25 = 8.5777777778, 149/19.3 = 7.7202072539, 515/65.2 = 7.8987730061
Abbiamo già usato questo metodo per studiare sperimentalmente ordini di infinito/infinitesimo
(
infiniti
Dati dotati di precisione
Sotto sono rappresentati graficamente i dati relativi allo studio di una macchina semplice, che trasforma una certa forza di intensità x (kg) in una forza minore, di intensità y (kg).
I valori di x sono 10, 17, 30, 47 con le precisioni 1, 1, 1, 1.5. I valori di y sono 4.4, 6.9, 11.6, 18.9 tutto con la precisione 0.2.
I valori sono quindi rappresentati con dei rettangolini.
Come posso descrivere la relazione
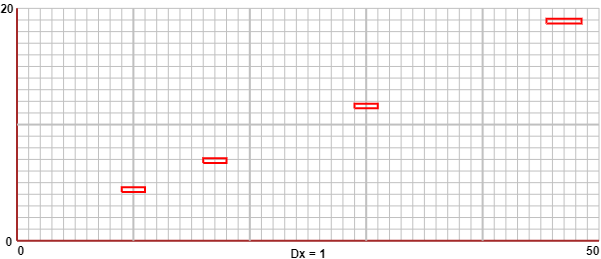
Devo tracciare le due rette di massima e di minima pendenza che passano per l'origine e per tutti i rettangolini.
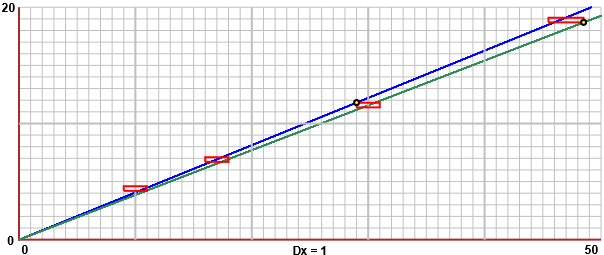
La retta di minima pendenza passa per (47+1.5,18.9-0.2); 18.7/48.5 = 0.38556… ≥ 0.38.
Quella di massima pendenza per (30-1,11.6+0.2); 11.8/29 = 0.40689… ≤ 0.41.
Senza utilizzare il grafico potremmo fare i calcoli con WolframAlpha:
max {(4.4-0.2)/(10+1), (6.9-0.2)/(17+1), (11.6-0.2)/(30+1), (18.9-0.2)/(47+1.5)}
0.385567
min {(4.4+0.2)/(10-1), (6.9+0.2)/(17-1), (11.6+0.2)/(30-1), (18.9+0.2)/(47-1.5)}
0.406897
Posso dedurre che y = k·x con 0.38 ≤ k ≤ 0.41.
Qui puoi trovare come sono stati fatti i grafici precedenti.
Qui abbiamo studiato l'individuazione dei parametri di una funzione lineare che si adatti ad
alcuni dati sperimentali. Il problema può essere esteso ad altri tipi di funzioni.
Eser.4 sol.
Eser.5 sol.
Eser.6 sol.
Eser.7 sol.
Eser.8 sol.
Eser.9 sol.
Eser.10 sol.
