Di seguito sono riportate due possibili critiche alla "definizione soggettivista". Quali considerazioni didattiche possono stimolare?
(1) Se la probabilità matematica fosse una misura quantitativa del grado di certezza del ricercatore,
allora la teoria della probabilità si ridurrebbe a qualcosa affine alla psicologia e tutte le conclusioni tratte da asserzioni
probabilistiche sarebbe private del loro contenuto oggettivo.
(2) La definizione così formulata non è una definizione matematica in quanto fa riferimento a concetti non matematici.
Vedi tutti e tre i commenti ai quesiti precedenti.
Riassumendo, spesso le osservazioni critiche sulle "definizioni" non "assiomatiche"
(cioè non basate su una elencazione di proprietà che deve soddisfare una misura di probabilità)
che appaiono nei libri sono fuori luogo e, a volte, contengono grossolani errori.
Il nocciolo della questione è, invece, che non siamo di fronte a "definizioni matematiche" in quanto
sono tutte riferite a considerazioni extra-matematiche (anche se la 2ª e la 3ª, non certo la 1ª,
con apparati matematici molto complessi, attraverso una matematizzazione del concetto di casualità
o mediante una formalizzazione nell'ambito della teoria dei giochi o …
potrebbero essere "trasformate" in definizioni matematiche).
Considerarle definizioni, invece che possibili approcci alla determinazione di alcuni valori di probabilità,
contribuisce a oscurare la comprensione sia della natura dei modelli matematici che del ruolo del calcolo delle probabilità.
Altro conto sarebbe (nel contesto di una riflessione più generale sui modelli matematici e sulla natura
della matematica) inquadrare storicamente queste "definizioni" come tentativi definitori tipici di un periodo in cui la matematica non
aveva ancora assunto un proprio status autonomo.
Per altro, se un insegnante è interessato a sviluppare le problematiche storiche, potrebbe essere utile
esaminare con gli alunni i primi problemi probabilistici formulati esplicitamente nel XVII secolo e le difficoltà incontrate da "matematici"
(o, meglio, "intellettuali" che si occupavano di scienza in generale, di tecnica e, in molti casi, anche di filosofia, letteratura,
;
il "matematico puro" non esisteva ancora) dell'epoca:
non comprensione del perché giocando con 3 dadi 10 viene più frequentemente di 9 (la perplessità
derivava dal fatto 9 può essere formato addizionando 6 diversi "insiemi" di numeri {1,2,6}, {1,3,5}, {1,4,4}, {2,2,5}, {2,3,4}, {3,3,3}
e che lo stesso vale per 10; non si teneva conto che le "terne ordinate" che danno luogo a 10 sono più di quelle che danno luogo a 9),
convinzione che lanciando due volte una moneta ci siano 2 possibilità su 3 di ottenere "testa",
Alcune considerazioni didattiche:
• i temi della statistica e della probabilità, che offrono una grande varietà
di attività di modellizzazione significative e realizzabili con tecniche matematiche elementari, possono avere un
ruolo importante nell'educazione matematica, nell'esplorazione delle abilità di matematizzazione degli alunni, nel recupero di motivazioni alla "matematica",
.
• esplorare i significati che gli alunni attribuiscono ai termini, mettere in luce le differenze
tra linguaggio comune e linguaggi specialistici,
è necessario per prevenire/superare confusioni concettuali, per evitare che la cultura
scolastica rimanga una cultura ad hoc, una parentesi temporanea senza interazioni con la vera cultura dei ragazzi,
.
• è bene non privilegiare problemi stereotipati e che privilegiano attività
di calcolo combinatorio presentate in forme banali e meccaniche (così come accade per le attività algebriche ridotte al "calcolo
delle espressioni") a scapito delle attività di matematizzazione e dello sviluppo della mentalità probabilistica; così come, ad es., è da
privilegiare la capacità di modellizzare problemi come quello di questo quesito
con tabelle, diagrammi di Venn, grafi,
piuttosto che la memorizzazione della formula di Bayes per risolverlo
(vedi sotto) e della associazione "meccanica" ad essa di problemi che abbiano una tale "struttura".
| P(A/B) = | P(A)·P(B/A) | = | 1%·95% | = 16.1% |
| ———————————————— | ———————— |
| P(A)·P(B/A)+P(NOT A)·P(B/NOT A) | 1%·95%+99%·5% |
|
• escludere dall'insegnamento le situazioni "probabilistiche" che si presentano nella vita quotidiana ma
non sono inquadrabili in schemi come "(n° casi favorevoli) / (n° casi possibili)" forse "semplifica" l'insegnamento, ma non anche
la comprensione e l'apprendimento; analogamente l'abuso dell'impiego di "a caso" come "a caso con distribuzione non uniforme" tende a favorire
misconcetti (anche se è vero che spesso si sottointende che "prendere a caso", ad esempio una carta in un mazzo o un nominativo in un elenco,
significhi farlo in modo uniforme, senza privilegiare alcuna "zona"; ma sarebbe meglio esplicitare qualche convenzione con gli alunni, del tipo:
"quando diremo «del tutto a caso» intenderemo che la distribuzione è uniforme").
• gli ineludibili legami con situazioni reali forniscono occasioni per ragionamenti "contestualizzati",
valutazioni "intuitive",
, favorendo la partecipazione anche degli studenti con più lacune tecniche iniziali senza essere noiosa per i "bravi"
(per interpretare dati, grafici,
non bastano le abilità di "calcolo"); consentono anche di interagire, più o meno esplicitamente,
con i "bisogni" degli adolescenti: la statistica (se riferita a situazioni significative) può costituire un supporto culturale che aiuti gli
alunni a razionalizzare e affrontare i problemi di inserimento sociale (confronto con gli altri,
, sia dal punto di vista dell'aspetto fisico
che da quelli delle situazioni economica, familiare,
) tipici della fase terminale dello sviluppo, e, quindi, può costituire anche un
elemento di motivazione allo studio della matematica.
• è importante far osservare che affrontando un problema (non deterministico) non sempre è
sufficiente il ricorso alla statistica e alla probabilità e, più in generale, mettere a fuoco la natura e i limiti dei modelli matematici.
• è utile far riflettere gli alunni sui pregiudizi da cui sono spesso affette le nostre
valutazioni, le immagini mentali con cui interpretiamo/ricostruiamo/registriamo ciò che vediamo,
, fare congetture e stime
con gli alunni prima di affrontare risoluzioni "rigorose";
• il ricorso al computer è didatticamente importante sia perché
è un modo in cui oggi si "fa" matematica,
|
| | si controllano risultati ottenuti per via teorica o si fanno valutazioni che sarebbe
troppo dispendioso ottenere per via teorica, si fanno esperimenti per congetturare o indirizzare la ricerca di proprietà, si realizzano vere
e proprie dimostrazioni, si costruiscono facilmente rappresentazioni grafiche, spesso preferite alle sintesi numeriche sia nella modellizzazione
di situazioni che nella comunicazione di informazioni,
|
sia, soprattutto, perché, per fare una simulazione, è necessario comprendere il problema, esplicitare le
ipotesi sottointese, dettagliare la traduzione "realtà" → "modello matematico",
|
• i temi della statistica e della probabilità è bene che non siano affrontati in modi
troppo separati (mentre la teoria della probabilità è essenzialmente la messa a punto di metodi indiretti per trovare, a partire
dalle probabilità note di alcuni eventi, la probabilità di altri eventi ad essi connessi: il punto di partenza è nella maggior
parte dei casi, una indagine di tipo statistico per individuare o convalidare alcune valutazioni probabilistiche iniziali);
• è opportuno implementare collegamenti/"sinergie" con altri temi matematici
(invece spesso gli insegnanti percepiscono il tema "probabilità e statistica" solo come "cose in più" rispetto ai
vecchi programmi); per esempi di collegamenti si pensi come nelle attività statistiche e, poi, in quelle probabilistiche,
sono presenti riferimenti a: rappresentazioni dei numeri, ordini di grandezza, approssimazioni, disequazioni,
;
al concetto di funzione (funzioni di diretta proporzionalità; funzioni lineari; tabelle di dati, cioè insiemi
di coppie; le funzioni, a uno e due argomenti, della calcolatrice; composizione di funzioni, funzioni inverse, somma di funzioni,…,
integrazione,…); alle rappresentazioni grafiche e a considerazioni riferite a simmetrie, traslazioni,
;
alla manipolazione di formule per rappresentare/trasformare procedimenti di calcolo;
;
ai concetti di derivazione e integrazione).
Confronto con le presentazioni (universitarie) standard (sigma-algebre, variabili casuali come funzioni, ecc.).
Il modo in cui abbiamo introdotto i concetti probabilistici di base è diverso dal modo in cui
usualmente vengono introdotti nei corsi universitari per "matematici".
In particolare abbiamo descritto le proprietà che devono avere gli eventi senza dare una definizione di che cosa sia
una famiglia di eventi, la qual cosa, come vedremo adesso, richiederebbe il concetto di σ-algebra, che è più semplice
descrivere attraverso una definzione insiemistica degli eventi (questa è l'unica motivazione "sensata" per un approccio insiemistico a questo concetto).
Quando, più avanti, vengono introdotte le funzioni di densità per il caso continuo, ci si limiterà agli integrali di Riemann,
mentre una trattazione più estesa richiederebbe di riferirsi agli integrali di Lebesgue.
Ricordiamo assai sinteticamente (chi vuole può approfondire questi concetti su un manuale universitario
di calcolo delle probabilità) che in genere si definiscono:
• σ-algebra su un insieme A ogni insieme di sottoinsiemi di A chiuso rispetto
all'unione numerabile e alla complementazione, e
• spazio di probabilità ogni coppia (Pr,S) con S σ-algebra e,
se A è l'insieme su cui S è σ-algebra, Pr funzione da S in [0,1] tale che Pr(A)=1 e,
se Ai è una famiglia numerabile di elementi di S tra loro disgiunti,
Pr(UAi)=ΣPr(Ai) (proprietà della additività).
Che Pr(Ø)=0 è una conseguenza:
Pr(Ø U A) = Pr(Ø)+Pr(A) in quanto Ø ed A sono disgiunti, Pr(A)=1 e, quindi, Pr(Ø)=0.
Analogamente se l'insieme E sta in S, e quindi vi sta anche l'insieme complementare E', Pr(E') = 1−Pr(E).
L'insieme A viene detto spazio degli eventi e i suoi elementi vengono detti eventi elementari.
Gli elementi di S vengono detti eventi e Pr viene detta probabilità
(nel caso in cui A sia finito si può prendere come S un'algebra booleana di sottoinsiemi di A, di cui
la famiglia di tutti i sottoinsiemi di A è un esempio). Dato l'evento E, l'evento complementare E' viene detto anche
evento contrario.
Ad es. nel caso del lancio di un dado posso prendere {1,2,
,6} come A e tutti i sottoinsiemi di A come S.
Se mi interessa solo studiare la parità delle uscite posso limitarmi a S={A,Ø,{1,3,5},{2,4,6}};
la probabilità che l'uscita sia pari o dispari è Pr({1,3,5}U{2,4,6})=Pr(A)=1.
Assai più complessa è l'interpretazione di questi concetti quando non si è nel caso discreto.
È richiesta una definizione molto generale di misura occorre almeno la misura di Lebesgue
(vedi) o di Stieltjes
(vedi) , necessaria per misurare
gli elementi di S che si possono ottenere nel caso in cui A sia un intervallo di numeri reali, cioè un segmento, una
semiretta o una retta, o sia un rettangolo o
.
In alcuni libri (purtroppo anche universitari) si trovano delle cose buffe, e gravi . In particolare sono spesso presenti questi
due errori. Da una parte viene definita la additività solo per il caso finito, invece che per quello numerabile
(escludendo casi banali, come quello del lancio di una moneta equa fino a che esce testa).
Dall'altra viene detto che una probabilità Pr ha come dominio l'insieme dei sottoinsiemi di A
(invece che una σ-algebra di A), il che vale solo nel caso numerabile (è come se, fissata una misura su R, tutti gli insiemi di numeri reali
fossero misurabili); del resto, nel caso in cui A = [5,7], che senso avrebbe cercare di definire Pr(E) per
un generico insieme E contenuto in [5,7]?
Le variabili casuali vengono definite come funzioni che a eventi associano numeri reali.
Nel caso del lancio di due dadi, possiamo considerare la funzione che ad ogni esito (m,n) associa il numero m+n.
Il concetto di variabile casuale serve essenzialmente a dare forma numerica agli esiti di esperimenti di tipo non numerico.
Precisando, nel caso dei due dadi avremmo lo spazio degli eventi A={(m,n) / m,n numeri naturali maggiori di 0 e minori di 7},
la σ-algebra S={sottoinsiemi di A}, la variabile casuale U definita come la funzione da A in R che a (m,n) associa m+n.
Gli eventi che noi abbiamo indicato con U=x, U<x,
ora sarebbero {(m,n) / U(m,n)=x},
{(m,n) / U(m,n)<x},
, anche se, in genere, questi eventi continuano a essere descritti con la stessa scrittura;
ma in questo caso "U=x" sarebbe una abbreviazione di "{(m,n) / U(m,n)=x}", in cui "=" ha poco a che fare con l'usuale simbolo di eguaglianza.
Nel caso del lancio di un dado, se interessa solo la parità degli esiti, invece di prendere
S = {A,Ø,{1,3,5},{2,4,6}} e considerare Pr(X) solo per gli X in S, si può: prendere come S tutto {sottoinsiemi di A};
porre U(n) uguale a 0 se n è pari, uguale a 1 altrimenti; considerare Pr(U=0), cioè
Pr({n / U(n)=0}, e Pr(U=1) invece di Pr({2,4,6}) e Pr({1,3,5}).
Abbiamo scelto di non utilizzare questa impostazione, in particolare di considerare le variabili casuali come "speciali" variabili
e gli eventi come condizioni piuttosto che come insiemi, per vari motivi:
• per un primo livello di approfondimento, in cui non si fa ricorso a concetti e teoremi di
teoria della misura, questa trattazione è più "comoda" (sarebbe, comunque, formalizzabile nei vari dettagli e utilizzabile
al posto della presentazione canonica);
• consente di esprimersi in un linguaggio vicino a quello in cui, "in situazione", vengono usualmente
formulati i problemi probabilistici; anche nelle modellizzazioni al computer gli eventi vengono presentati in forma "logica", non "insiemistica";
• evita le difficoltà concettuali legate al chiamare "casuali" le variabili casuali, che,
nell'impostazione standard, non hanno nulla di casuale: ad esempio la variabile casuale più impiegata è la funzione identità
(nel caso del lancio di un dado, del tempo di attesa tra due arrivi a uno sportello, della misura di una grandezza fisica,
l'uscita è già numerica);
«il termine "casuale" è usato meramente per ricordare che l'insieme [su cui è definita la funzione] è uno spazio di eventi»
(dal noto manuale di analisi matematica di Apostol);
• evita difficoltà concettuali e notazionali legate al fatto che al cambiare dello spazio di eventi cambia
la misura di probabilità; in particolare non si può usare lo stesso simbolo Pr per rappresentare funzioni che hanno domini diversi;
anche in molti manuali universitari si trovano, invece, espressioni del tipo "Pr(X<x, Y<y) = Pr(X<x)·Pr(Y<y)" dove
la Pr a sinistra di "=" rappresenta un'altra funzione rispetto alla Pr a destra di "=" (e dove "Pr(X<x, Y<y)", che nella presentazione
che abbiamo utilizzato nel corso diventerebbe Pr(X<x AND Y<y), è un'altra abbreviazione spesso non spiegata).
L'impostazione richiamata in questo paragrafo ha anche lo scopo di formalizzare in modo unitario le variabili casuali.
In particolare tutte le variabili casuali ammetterebbero funzione di ripartizione cumulata definita in R.
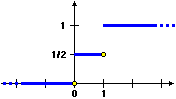
Ad es. nel caso della variabile U dell'ultimo esempio (U vale 0 se l'uscita del dado è pari, vale 1 se è dispari) la funzione di ripartizione è:
|
x → 0
x → 1/2
x → 1 |
se x<0
se 0≤x<1
se 1≤x |
(Pr(U≤x)=Pr({n/U(n)≤x})=Pr(Ø)=0),
(Pr(U≤x)=Pr({2,4,6})=1/2),
(Pr(U≤x)=Pr({1,2,
,6})=1). |
 |
Ma per una trattazione unitaria esauriente è necessaria l'introduzione di un concetto
più generale di integrale (integrale di Lebesgue-Stieltjes), cosa che viene fatta solo in corsi universitari avanzati.
Ad esempio esso serve per introdurre i concetti di media e varianza a partire dalla funzione di ripartizione cumulata,
così da comprendere in un'unica trattazione variabili casuali discrete e continue, e anche casi di variabili né
discrete né continue (ad es. alcune variabili a valori in un intervallo per le quali non esiste la funzione di densità).
Naturalmente questa trattazione, che deve essere affrontata da chi fa studi universitari
matematici o fisici, deve essere preceduta, nei livelli scolastici precedenti e all'inizio dell'università,
da una presentazione in cui non si ricorre a questi concetti.
|
