Il concetto di "probabilità"

  Nei giochi e nella "realtà" spesso si hanno da fare scelte di cui non si sanno prevedere esattamente le conseguenze (quale carta conviene scartare? in quale orario conviene partire per incontrare meno traffico in autostrada? …) o, comunque, si hanno da affrontare fenomeni di cui non si sa prevedere esattamente lo sviluppo (l'uscita di un dado, l'evolvere del tempo atmosferico, …).
    La parte della matematica che si occupa degli strumenti che permettono di razionalizzare le interpretazioni dei (e le scelte di fronte ai) fenomeni casuali (cioè di affrontarle ricorrendo alla ragione invece che affidandosi a pregiudizi, a superstizioni o al fato) è detta calcolo delle probabilità.
    Gli strumenti impiegati hanno una stretta parentela con quelli utilizzati nelle elaborazioni statistiche. Partiamo da tre semplici esempi.

Primo esempio.  Sta per disputarsi la partita Roma-Juventus. Gigi ritiene che la Roma 30 su 100 vincerà e 40 su 100 pareggerà. Qual è la probabilità per Gigi che vinca la Juventus?  Se da 100 tolgo 30 e 40 rimangono 30: per lui la Juve vince al 30 per 100. Volendo sintetizzare con qualche formula, uso Pr(…) per indicare la probabilità per Gigi che avvenga "…", indico con E l'esito della partita, che potrà essere "1", "2" o "X" (caratteri con cui indico rispettivamente la vittoria, la sconfitta o il pareggio della squadra di casa) ho:

Pr(E="1") = 30%,  Pr(E="X") = 40%,  Pr(E="1" OR E="X") = 30%+40% = 70%,  Pr(E="2") = 1 – Pr(E="1" OR E="X") = 1 – 70% = 30%.

| 1 | X | 2 | ||||||||||||||||||||||||||||||||||||||||||| | 3 0 % | 4 0 % | ? |

  Secondo esempio.  Voglio effettuare uno studio sociologico sui giovani e in questo ambito mi interessa valutare (1) la probabilità che un generico studente universitario si laurei compiuti i 29 anni e (2) quella che si laurei tra i 24 anni e mezzo e i 27 anni e mezzo. Considero l'istogramma, ovvero il box-plot (vedi figure sottostanti a destra), e ipotizzo (in assenza di altre informazioni) che anche ai nostri giorni e nei prossimi anni l'età di laurea si distribuisca in modo simile. Indico con E l'età di laurea e con  Pr(29 < E)  (o Pr(E>29)) e  Pr(24.5 ≤ E ≤ 27.5)  le due probabilità cercate.

(1)  Dal box-plot ricavo che il 75° percentile è poco più di 29 anni. Posso quindi stimare che la probabilità Pr(E≤29) di laurearsi al più a 29 anni sia grosso modo 75%=0.75.    Da qui (vedi figura sotto a sinistra) posso ricavare la stima che Pr(29<E) = 100%–75% = 25% (se il 75% degli studenti ha E≤29 i rimanenti 25% hanno E>29).
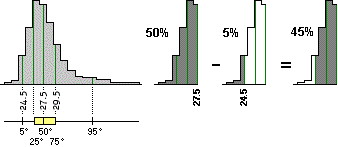(2)  Dal box-plot ricavo che 24.5 (24 anni e mezzo) e 27.5 sono il 5° e il 50° percentile deducendone che Pr(E≤24.5)=5% e Pr(E≤27.5)=50%.     Gli studenti che si laureano tra 24.5 e 27.5 anni si ottengono sottraendo quelli che si laureano con meno di 24.5 anni da quelli che si laureano con meno di 27.5 anni (vedi figura sopra a destra); quindi: Pr(24.5≤E≤27.5) = Pr(E≤27.5)–Pr(E<24.5) = 50%–5% = 45%. Posso concludere che Pr(24.5 ≤ E ≤ 27.5) ≈ 45%.

  Terzo esempio.  Voglio valutare la probabilità che lanciando un dado esca un numero pari. Suppongo che il dado sia equo, ovvero non sia truccato. Ciò significa supporre che l'uscita U abbia uguale probabilità di essere 1, 2, … o 6:
Pr(U=1) = Pr(U=2) = … = Pr(U=6).    Sia p il valore di questa probabilità.
Poiché  Pr(U=1)+Pr(U=2)+…+Pr(U=6) = 100% = 1, ho p+p+…+p = 6p = 1, da cui p=1/6.
Cioè:  Pr(U=1) = Pr(U=2) = … = Pr(U=6) = 1/6   Per trovare la probabilità che l'uscita sia pari posso fare:
Pr(U è pari) =Pr(U=2) + Pr(U=4) + Pr(U=6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2.

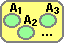
Posso rappresentare l'ipotesi che il dado sia equo con la figura a lato. Infatti l'ipotesi equivale a supporre che le uscite che si ottengono lanciando ripetutamente un dado tendano a distribuirsi secondo un istogramma in cui tutte le colonne abbiano la stessa altezza. La probabilità che un'uscita sia pari equivale alla somma delle frequenze delle colonne 2, 4 e 6, che corrispondono a metà della superficie dell'istogramma, ossia questa probabilità vale 50%.

  Nel primo e nel secondo degli esempi precedenti ho associato ad alcuni eventi A un numero compreso tra 0 e 1 (=100%) come Pr(A) (probabilità di A).  Nel terzo ho fissato delle condizioni sulla funzione A → Pr(A): ho supposto che Pr(U=1) = Pr(U=2) = ….
    In tutti i casi ho poi dedotto le probabilità relative ad altri eventi applicando a Pr alcune delle proprietà che si erano già usate per le frequenze percentuali.
    Rivediamo più sistematicamente queste proprietà.

	• Pr(NOT A) = 100% – Pr(A) • Pr(A OR NOT A) = 100% =1 • Pr(A AND NOT A) = 0
Esempio:  Pr(E>29) = Pr(NOT E≤29) = 100% – Pr(E≤29)
	• Pr(A1 OR A2 OR A3 OR …) = Pr(A1) + Pr(A2) + Pr(A3) + … se  A1, A2, A3, … sono tra loro incompatibili, cioè se due qualunque eventi Ai e Aj non possono essere veri contemporaneamente.
Esempio:  Pr(U è pari) = Pr(U=2 OR U=4 OR U=6) = Pr(U=2)+Pr(U=4)+Pr(U=6)

   Quest'ultima proprietà è nota come proprietà additiva.

   La proprietà additiva vale nel caso di una sequenza A₁, A₂, A₃, … di eventi finita o infinita.  Ad esempio consideriamo una moneta truccata in cui testa esca con probabilità 0.9; lancio ripetutamente la moneta fino a che non esce "testa"; la probabilità che esca testa al primo lancio è 0.9 e quella che non esca è 0.1.  Anche al secondo lancio, che viene effettuato con probabilità 0.1, la probabilità che esca testa è 0.9.  Quindi la probabilità che esca testa nei primi due lanci è 0.9+0.1·0.9 = 0.9+0.09 = 0.99, e che non esca è 0.01.  In quest'ultimo caso effettuo un terzo lancio, e con probabilità 0.9 esce testa. Quindi la probabilità che esca testa nei primi tre lanci è 0.9+0.09+0.01·0.9 = 0.9+0.09+0.009 = 0.999.  Analogamente la probabilità che esca al quarto lancio è 0.9+0.09+0.009+0.0009 = 0.9999.  La probabilità che prima o poi esca testa è pari alla somma infinita 0.9+0.09+0.009+0.0009+0.00009+… = 0.999… = 1, ovviamente.

   Una proprietà analoga vale per le aree: se unisco dei poligoni l'area della figura risultante è la somma delle loro aree solo se essi non sono sovrapposti:

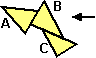Area(A U B U C) = Area(A) + Area(B) + Area(C) Area(A U B U C) ≠ Area(A) + Area(B) + Area(C)

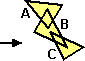   Vediamo una situazione in cui non si può applicare l'additività.  Conosco le percentuali degli studenti con insufficienze in matematica (42%), in fisica (39%) e in entrambe le materie (28%) del primo quadrimestre dell'anno passato nella scuola KK. Voglio valutare la probabilità che quest'anno uno studente debba essere coinvolto in corsi di recupero nell'area matematico-fisica, cioè valutare Pr(S∈ M OR S∈F) (ho indicato con S un generico studente, con M l'insieme di quelli insufficienti in matematica e con F quello degli insufficienti in fisica).
   Non posso usare la proprietà additiva e fare Pr(S∈M)+Pr(S∈F) poiché si può essere insufficienti in entrambe le materie, ma devo fare:
Pr(S∈M OR S∈F) = Pr(S∈M) + Pr(S∈F) – Pr(S∈M AND S∈F) = 42%+39%–28% = 53%
[il 28% degli insufficienti in entrambe è conteggiato due volte, devo dunque toglierne una]

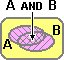Più in generale, di fronte a valutazioni del tipo Pr(A OR B) con A e B eventi non incompatibili, si usa la proprietà: •  Pr(A OR B) = Pr(A) + Pr(B) – Pr(A AND B)

    Questa proprietà come abbiamo visto, è una conseguenza delle altre evidenziate col pallino (•).  Anche la terza proprietà  (Pr(A AND NOT A) = 0)  è una conseguenza delle altre: prova a pensarci e arriverai facilmente a questa conclusione.

  Naturalmente, a seconda di come si scelgono le valutazioni iniziali, per la stessa situazione si possono ottenere diverse misure di probabilità. Le valutazioni iniziali possono essere dedotte dall'esperienza o da considerazioni di tipo fisico o da propri convincimenti o … . Devono comunque essere tali da non condurre a contraddizioni: a partire da esse, applicando ripetutamente le proprietà elencate nel punto precedente, non posso ottenere valutazioni diverse per uno stesso evento, non posso ottenere probabilità negative o superiori al 100%, … (ad es. non posso valutare 60% la probabilità che nella prossima partita Roma-Lazio vinca la Roma e 50% che pareggino; verrebbe contraddetta la prima proprietà).
Si osservi che il ruolo delle valutazioni iniziali mostra come anche in questo caso, come in altri discussi in altre voci, le conoscenze matematiche non sono di per sé sufficienti per modellizzare o risolvere "razionalmente" un problema.

La caratterizzazione del concetto di probabilità descritta sopra (non defininendo che cos'è la "probabilità" ma elencando le proprietà che deve avere una "misura di probabilità") è simile alla caratterizzazione di altri oggetti matematici (abbiamo visto ad esempio che vi sono diversi modi di definire una "distanza" tra due punti o, addirittura, diversi modi di definire uno "spazio"). Vedrai più avanti che le proprietà sopra elencate che deve avere una misura di probabilità per essere considerata tale vengono chiamate assiomi. Vedrai come anche lo spazio ed altri oggetti matematici possono essere definiti in questo modo: non esplicitando che cosa sono ma esplcitando le proprietà che essi devono soddisfare.