Continuità
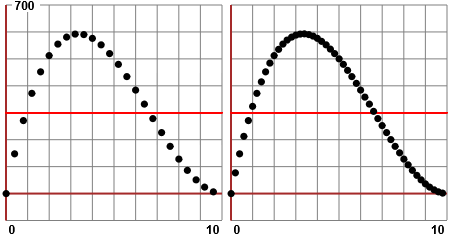
 Tracciando
il grafico di F: x → (20–2x)2x per punti, aumentando man mano il numero dei punti tracciati (cioè
Tracciando
il grafico di F: x → (20–2x)2x per punti, aumentando man mano il numero dei punti tracciati (cioè
 infittendo le x tabulate), arrivo a ottenere una figura
formata da una sequenza di pallini attaccati, senza spazi bianchi in
mezzo; sotto il tracciamento, con pallini di una certa dimensione, suddividendo l'intervallo [0,10] in 25, 50, 100 e 200 intervallini. Se i pallini sono più piccoli ne dovrò tracciare una quantità maggiore. In particolare trovo sicuramente intersezioni con il
grafico di x → 300, e con quello di ogni altra funzione x → k con k compreso tra due qualunque output di F.
infittendo le x tabulate), arrivo a ottenere una figura
formata da una sequenza di pallini attaccati, senza spazi bianchi in
mezzo; sotto il tracciamento, con pallini di una certa dimensione, suddividendo l'intervallo [0,10] in 25, 50, 100 e 200 intervallini. Se i pallini sono più piccoli ne dovrò tracciare una quantità maggiore. In particolare trovo sicuramente intersezioni con il
grafico di x → 300, e con quello di ogni altra funzione x → k con k compreso tra due qualunque output di F.
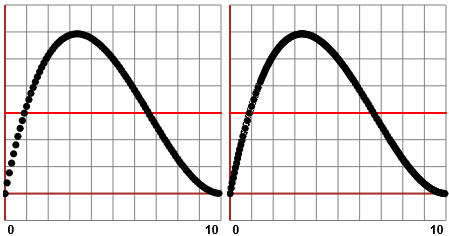
Se una funzione in un intervallo [a,b] è definita e all'infittire comunque
degli input in tale intervallo, comunque piccoli si prendano i "pallini", fornisce output man mano più
fitti, come x → (20–2x)2x in [0,10], si dice che tale funzione è continua in [a,b].
Si può dimostrare che questa condizione comporta che, presi comunque x1 e x2 in [a,b] e un valore k compreso tra F(x1) e F(x2), il grafico di F interseca la retta y=k almeno in un punto
(questa proprietà è nota come teorema di Bolzano,
dal nome del matematico, filosofo ed altro, boemo, nato nel 1781 e morto nel 1848, che l'ha provata).
Intuitivamente possiamo esprimere la continuità di F
dicendo che il grafico di F nell'intervallo [a,b] è una curva priva di "buchi". | | 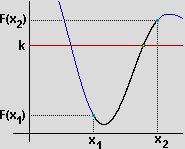 |
Se una funzione è definita su R ed è continua in ogni intervallo
[a,b], diciamo che è continua in R, ossia in (-∞,∞).
Le idee ora sviluppate sono già state usate in voci precedenti:
in  funzione(1) abbiamo visto
come infittendo gli input di x → x²
si può trovare con la precisione che si vuole il numero positivo x tale
che x² = 5 (in pratica abbiamo trovato l'ascissa di uno dei due punti
in cui il grafico della funzione interseca la retta y = 5);
le abbiamo utilizzate anche in funzione(1) abbiamo visto
come infittendo gli input di x → x²
si può trovare con la precisione che si vuole il numero positivo x tale
che x² = 5 (in pratica abbiamo trovato l'ascissa di uno dei due punti
in cui il grafico della funzione interseca la retta y = 5);
le abbiamo utilizzate anche in  risoluz.equazioni(1) per trovare dove un certo
grafico interseca l'asse x.
risoluz.equazioni(1) per trovare dove un certo
grafico interseca l'asse x. |
 La funzione f rappresentata graficamente
all'inizio della voce
La funzione f rappresentata graficamente
all'inizio della voce  funzione (1) (tariffario) non è
continua in [0, 600], così come il "troncamento agli interi" non è continuo (vedi
questa animazione con il tracciamento di tale funzione
e quello di una funzione continua).
funzione (1) (tariffario) non è
continua in [0, 600], così come il "troncamento agli interi" non è continuo (vedi
questa animazione con il tracciamento di tale funzione
e quello di una funzione continua).
Non sono continue le funzioni che rappresentano
 segnali digitali:
segnali digitali:
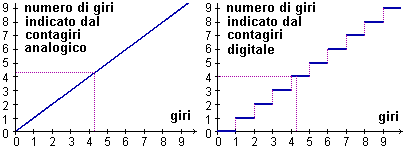
Vi sono funzioni che sono continue solo in una parte del loro dominio.
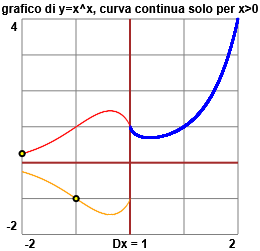
In  funzione (1)
abbiamo già considerato la funzione x → xx, rappresentata graficamente a fianco,
che, nonostante le apparenze, è continua solo in [0,∞) (ovvero in ogni intervallo
[0,k) con k>0). A sinistra di x=0
la funzione definita solo sui numeri razionali e ha comportamenti diversi su certi numeri razionali e su altri (sembra avere per grafico
due rami di curva mentre in realtà sono insiemi di punti fittissimi). funzione (1)
abbiamo già considerato la funzione x → xx, rappresentata graficamente a fianco,
che, nonostante le apparenze, è continua solo in [0,∞) (ovvero in ogni intervallo
[0,k) con k>0). A sinistra di x=0
la funzione definita solo sui numeri razionali e ha comportamenti diversi su certi numeri razionali e su altri (sembra avere per grafico
due rami di curva mentre in realtà sono insiemi di punti fittissimi).
Ad esempio in -2 vale (-2)-2 = 1/(-2)² = 1/4 e in -1 vale (-1)-1 = 1/(-1) = -1.
| |  |
 Tutte le funzioni del tipo x → f(x) con f(x) termine costruito (a partire da x e da costanti) solo mediante applicazioni delle "quattro operazioni" o dell'elevamento a potenza e della radice quadrata (o, anche, delle funzioni seno, coseno, tangente) sono continue in ogni intervallo
[a,b] in cui siano definite. In particolare le funzioni
polinomiali sono continue in tutto R, cioè in ogni intervallo
[a,b].
Tutte le funzioni del tipo x → f(x) con f(x) termine costruito (a partire da x e da costanti) solo mediante applicazioni delle "quattro operazioni" o dell'elevamento a potenza e della radice quadrata (o, anche, delle funzioni seno, coseno, tangente) sono continue in ogni intervallo
[a,b] in cui siano definite. In particolare le funzioni
polinomiali sono continue in tutto R, cioè in ogni intervallo
[a,b].
Ciò segue da come abbiamo definito le operazioni tra numeri reali
( e
e
 ).
Ad es. il valore di x·x è quel numero a cui mi avvicino sempre più man mano che calcolo x·x con x approssimazione di x man mano migliore;
da ciò si può dedurre che all'infittire dei valori di x si infittiscono i valori di x·x, e quindi che x → x·x è una funzione continua.
).
Ad es. il valore di x·x è quel numero a cui mi avvicino sempre più man mano che calcolo x·x con x approssimazione di x man mano migliore;
da ciò si può dedurre che all'infittire dei valori di x si infittiscono i valori di x·x, e quindi che x → x·x è una funzione continua.
Anche il  procedimento per il calcolo di 2x con x numero reale considerato in una voce precedente si basa sul fatto che si vuole che la funzione x → 2x sia continua.
procedimento per il calcolo di 2x con x numero reale considerato in una voce precedente si basa sul fatto che si vuole che la funzione x → 2x sia continua.
 È evidente dalle considerazioni svolte
È evidente dalle considerazioni svolte  all'inizio di questa voce (F(x)=300 ha soluzioni poiché F è continua e ha output maggiori e minori di 300) che il concetto di continutà è importante nello studio della
all'inizio di questa voce (F(x)=300 ha soluzioni poiché F è continua e ha output maggiori e minori di 300) che il concetto di continutà è importante nello studio della  risoluzione delle equazioni e in varie questioni di geometria.
risoluzione delle equazioni e in varie questioni di geometria.
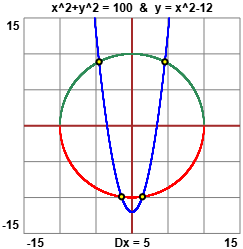
Consideriamo il  sistema seguente: sistema seguente:
| { | x2 + y2 = 100
y = x2 – 12 |
Osservando i grafici delle due equazioni, possiamo concludere che il sistema ha 4 soluzioni. Ma, ad essere rigorosi, il solo fatto che dalle rappresentazioni grafiche si veda che una curva "scavalca" l'altra non ci assicura che effettivamente tale curve abbiano ivi un punto in comune.
Tuttavia la parabola e il cerchio sono curve "continue", senza "buchi": la prima è il grafico di una funzione continua, mentre la seconda è  l'unione dei grafici delle due funzioni continue: l'unione dei grafici delle due funzioni continue:
x → √(100 – x2) e x → – √(100 – x2). |
 |
Esercizi: testo1 e soluzione, testo2 e soluzione
 Tracciando
il grafico di F: x → (20–2x)2x per punti, aumentando man mano il numero dei punti tracciati (cioè
Tracciando
il grafico di F: x → (20–2x)2x per punti, aumentando man mano il numero dei punti tracciati (cioè
 infittendo le x tabulate), arrivo a ottenere una figura
formata da una sequenza di pallini attaccati, senza spazi bianchi in
mezzo; sotto il tracciamento, con pallini di una certa dimensione, suddividendo l'intervallo [0,10] in 25, 50, 100 e 200 intervallini. Se i pallini sono più piccoli ne dovrò tracciare una quantità maggiore. In particolare trovo sicuramente intersezioni con il
grafico di x → 300, e con quello di ogni altra funzione x → k con k compreso tra due qualunque output di F.
infittendo le x tabulate), arrivo a ottenere una figura
formata da una sequenza di pallini attaccati, senza spazi bianchi in
mezzo; sotto il tracciamento, con pallini di una certa dimensione, suddividendo l'intervallo [0,10] in 25, 50, 100 e 200 intervallini. Se i pallini sono più piccoli ne dovrò tracciare una quantità maggiore. In particolare trovo sicuramente intersezioni con il
grafico di x → 300, e con quello di ogni altra funzione x → k con k compreso tra due qualunque output di F.





