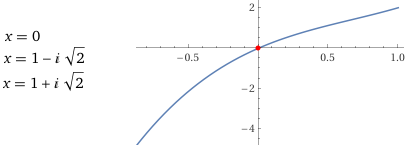
Calcola (a mano, e controlla, poi, con WolframAlpha) le soluzioni (reali o complesse) della equazione in x  x³ - 2·x² + 3·x = 0

x³-2·x²+3·x = x·(x²-2·x+3).  Qundi x³-2·x²+3·x = 0 equivale a  x=0 OR x²-2·x+3=0

Ricordo che le soluzioni di  a·x² + b·x + c = 0 sono:

x = - b —— 2a ± √(b2 - 4ac) ——————————— 2a

Nel nostro caso x²-2·x+3=0 avrebbe le soluzioni  1 ± √(-8)/2 = 1 ± √(-2·4)/2 = 1 ± √(-2)
Qual è il numero complesso x che al quadrato faccia -2?  Quello che al quadrato fa -1 è i, quindi quello che al quadrato fa -2 è √2 i.
In definitiva, 0 è l'unica soluzione reale, mentre le soluzioni complesse sono  0, 1+√2 i, 1-√2 i.

Con WolframAlpha:   solve x^3 - 2*x^2 + 3*x = 0  →