La Terra nelle proiezioni cilindriche

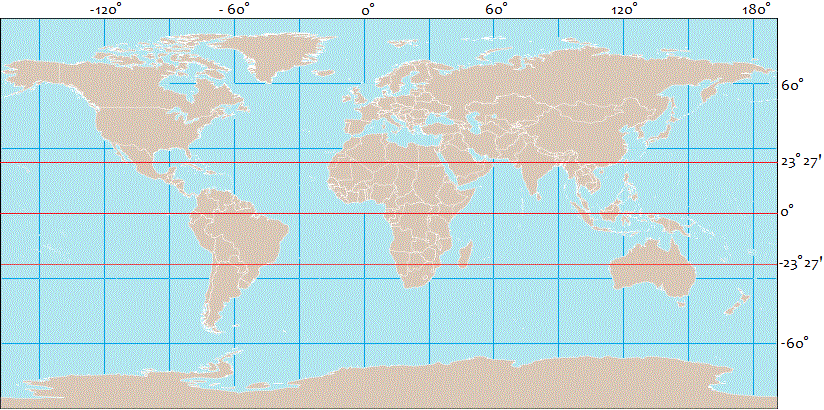
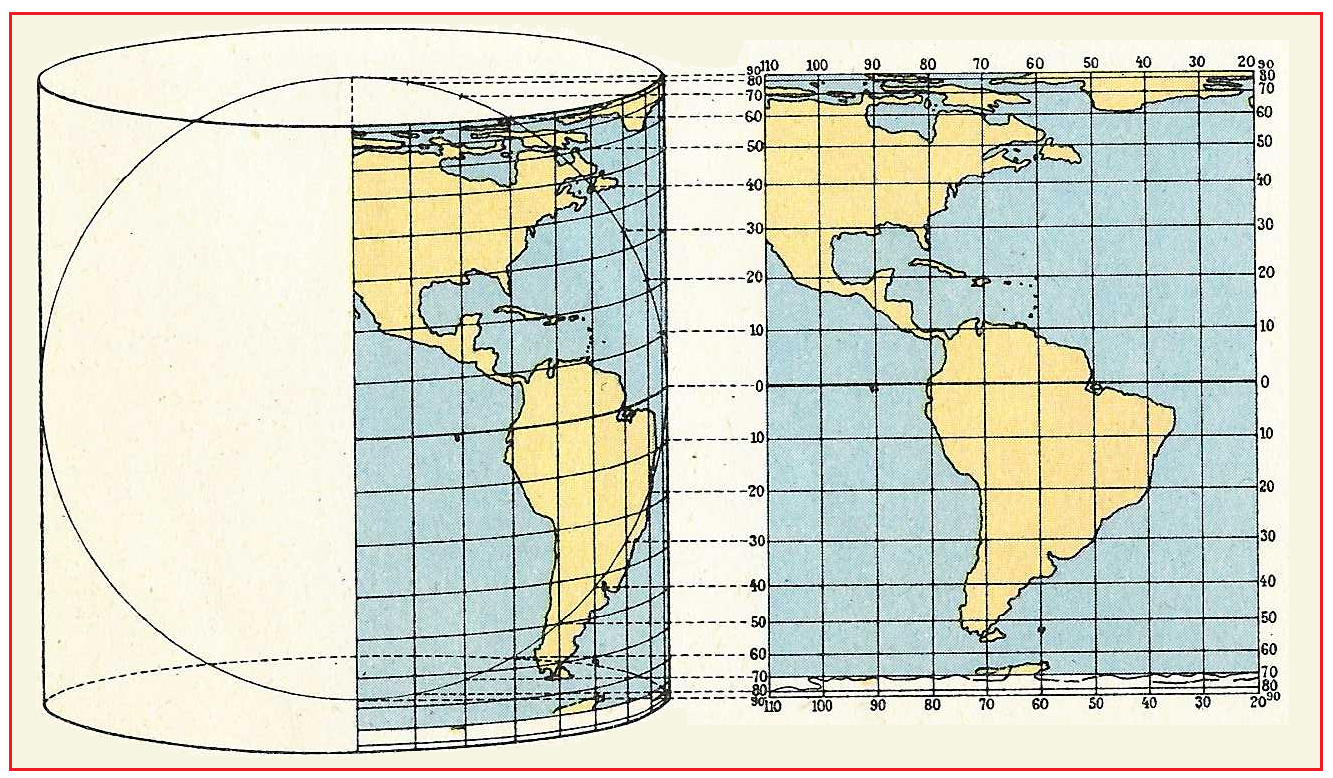
    Avrai già visto carte geografiche come quella rettangolare qui sotto a sinistra.  A destra come è stata ottenuta:  proiettando i confini dei vari continenti su un cilindro e poi srotolando il cilindro.

    Questa rappresentazione viene chiamata proiezione cilindrica equivalente (o proiezione di Lambert, cartografo svizzero che l'ha descritta in un manuale nel 1772).  L'aggettivo "equivalente" è dovuto al fatto che questa rappresentazione ha la proprietà di conservare le aree:  una figura sulla sfera viene proiettata in una figura sul cilindro (che può poi essere srotolata in forma piana) che ha la sua stessa area.  Quindi, in particolare, se una regione ha area doppia di un'altra anche le loro rappresentazioni ottenute con questa proiezione sono l'una di area doppia dell'altra.

    Verifichiamo la cosa concretamente (si potrebbe anche darne una dimostrazione, ma questa sarebbe affrontabile solo alla fine delle scuole superiori).  Consideriamo l'America del Sud e l'Africa, escludendo per semplicità l'isola di Madagacscar.  Se consultiamo un manuale o cerchiamo su Internet, troviamo che la prima ha un'estensione di 17805 km² e la seconda di 29634 km².  Il rapporto tra la seconda e la prima area è 1.664363942713, arrotondando a 5 cifre 1.6644.
    Consideriamo la rappresentazione delle due regioni geografiche sulla proiezione cilndrica equivalente:

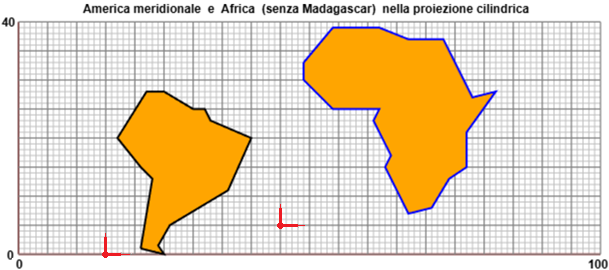
    Questa cartina è stata ottenuta segnando con alcuni punti su un foglio di carta millimetrata trasparente i contorni delle due regioni come appaiono su una proiezione cilindrica.  Poi, uitilizzando un programmino (vedi qui, se vuoi), si sono rappresentate le figure che congiungono i punti.  Per l'America Meridionale, utilizzando le coordinate a partire dal punto segnato in rosso a sinistra, si sono ottenute le coordinate in millimetri:
x: 6,10, 9,11,21,25,18,17,15,10, 7, 2, 6, 8,6
y: 1, 0, 1.5,5,11,20,23,25,25,28,28,20,15,13,1
    Per l'Africa, partendo dal secondo punto segnato in rosso, si sono ottenute:
x:  4, 4, 9,17,16,19,18,22,26,29,32,32,37,33,28,22,17, 9, 4
y: 28,25,20,20,18,12,10, 2, 3, 8,10,16,23,22,32,32,34,34,28

    Date le coordinate, posso ottenere le due aree (in mm²) con lo script "area polig" presente qui.  Ottengo:
area = 327.25   e   area = 546.5    da cui   546.5/327.25 = 1.669977081742, arrotondando 1.670.

I due valori trovati (1.6644 e 1.670) sono "praticamente" uguali (tenendo conto delle approssimazioni con cui abbiamo rappresentato le due figure).