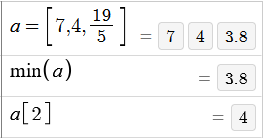Calcolatore (5) - Grafica, …
 Coordinate schermo (concrete) e cartesiane (virtuali)
Coordinate schermo (concrete) e cartesiane (virtuali)
Con un computer si possono disegnare, muovere e trasformare figure. Nella voce  calcolatore (4) abbiamo visto come un'immagine che appare sullo schermo è digitalizzata.
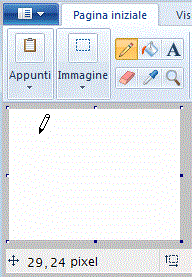
Sotto a sinistra è riprodotto il momento in cui, con un programma per costruire immagini, si sta tracciando un punto-pixel (il puntatore del mouse ha assunto l'aspetto di una matita).
In fondo alla finestra associata alla applicazione appaiono le coordinate-schermo del pixel (29 e 24 in questo caso): sono
i numeri d'ordine della colonna e della riga in cui è collocato; le colonne vengono numerate a partire da sinistra
iniziando con il numero 0; analogamente, a partire dall'alto (non dal
basso!), vengono numerate le righe.
calcolatore (4) abbiamo visto come un'immagine che appare sullo schermo è digitalizzata.
Sotto a sinistra è riprodotto il momento in cui, con un programma per costruire immagini, si sta tracciando un punto-pixel (il puntatore del mouse ha assunto l'aspetto di una matita).
In fondo alla finestra associata alla applicazione appaiono le coordinate-schermo del pixel (29 e 24 in questo caso): sono
i numeri d'ordine della colonna e della riga in cui è collocato; le colonne vengono numerate a partire da sinistra
iniziando con il numero 0; analogamente, a partire dall'alto (non dal
basso!), vengono numerate le righe.
 Come viene memorizzata una immagine? Oltre che memorizzarla pixel per pixel, se ne possono memorizzare solo alcuni punti
mediante i quali, con opportuni programmi, si può ricostruire
l'intera immagine.
Come viene memorizzata una immagine? Oltre che memorizzarla pixel per pixel, se ne possono memorizzare solo alcuni punti
mediante i quali, con opportuni programmi, si può ricostruire
l'intera immagine.
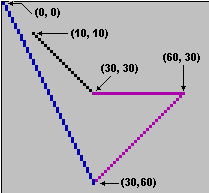
Ad esempio nel caso della figura precedente si possono memorizzare in un file le coordinate dei soli punti (10,10), (30,30), (60,30), (30,60) e (0,0); per vedere l'immagine si può poi utilizzare una applicazione che legga dal file le coordinate dei punti e man mano, in modo simile al programma sopra riprodotto,
li congiunga con dei segmenti.
Con WolframAlpha (vedi) introducendo solamente:
(10,10); (30,30); (60,30); (30,60); (0,0)
ottengo il grafico sottostante a sinistra, con i punti non collegati:
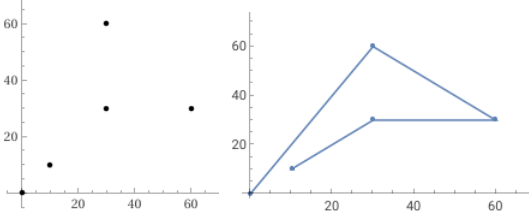
introducendo:
plot (10,10); (30,30); (60,30); (30,60); (0,0)
ottengo il grafico soprastante a destra, con i punti collegati, ma con una scala non monometrica.
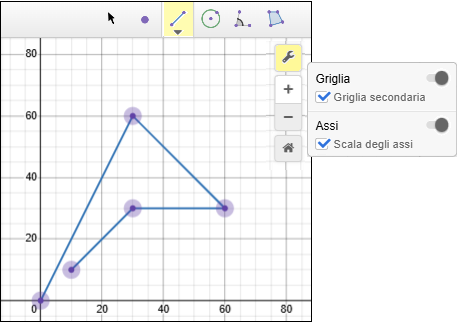
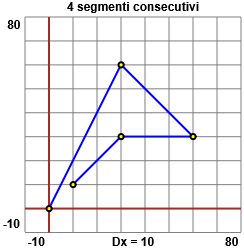
Con Desmos (vedi), scegliendo il sottoprogramma
Geometria, posso ottenere la figura sottostante a sinistra:
Invece la figura a destra è stata ottenuta con questo script.
 Confrontando queste con le figure precedenti si noti che i punti non vengono rappresentati
in corrispondenza dei pixel aventi le loro coordinate come coordinate-schermo (del resto la "scala" in queste applicazioni
può essere modificata) e che l'immagine appare capovolta: queste (e altre) applicazioni matematiche accettano input
in coordinate virtuali, cioè coordinate cartesiane usuali e poi le trasformano automaticamente,
in base alla scala scelta, in coordinate-schermo,
cioè nelle coordinate che individuano concretamente la posizione dei punti da visualizzare
(al loro interno sono presenti sottoprogrammi per il cambio di coordinate
costituiti da istruzioni che descrivono un procedimento sostanzialmente simile a quello che si deve fare per tracciare a
mano un grafico su carta millimetrata o quadrettata: scegliere la porzione di foglio, scegliere la scala, calcolare delle distanze, …).
Confrontando queste con le figure precedenti si noti che i punti non vengono rappresentati
in corrispondenza dei pixel aventi le loro coordinate come coordinate-schermo (del resto la "scala" in queste applicazioni
può essere modificata) e che l'immagine appare capovolta: queste (e altre) applicazioni matematiche accettano input
in coordinate virtuali, cioè coordinate cartesiane usuali e poi le trasformano automaticamente,
in base alla scala scelta, in coordinate-schermo,
cioè nelle coordinate che individuano concretamente la posizione dei punti da visualizzare
(al loro interno sono presenti sottoprogrammi per il cambio di coordinate
costituiti da istruzioni che descrivono un procedimento sostanzialmente simile a quello che si deve fare per tracciare a
mano un grafico su carta millimetrata o quadrettata: scegliere la porzione di foglio, scegliere la scala, calcolare delle distanze, …).
 Paint e Draw
Paint e Draw
Le
applicazioni per la grafica sono classificabili in due tipi: di tipo
paint (dipinto) o bitmap (mappa di bit)
e di tipo draw (disegno) o vettoriale.
Le applicazioni "paint" registrano le
immagini pixel per pixel. Se (con opportuni comandi) traccio un rettangolo (o un poligono) e poi un segmento ottenendo una figura simile a quella sotto indicata con (1), questa viene identificata con l'insieme dei pixel colorati in nero: non posso più separare segmento e poligono in quanto questi sono stati "fusi" in un'unica figura; posso - vedi (2) - selezionare con il mouse una parte di questa figura costituita da parti di poligono e di segmento e - vedi (3) - spostarla (traslarla).
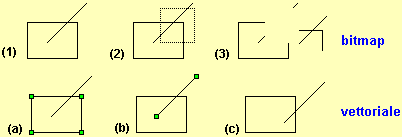
Una applicazione "draw", invece, memorizza il poligono [o un'altra figura] non come insieme di pixel, ma con tre tipi di informazione: l'informazione che si tratta di un poligono [o la categoria di figura], quella costituita dalla sequenza delle coordinate dei suoi vertici [o le informazioni quantitative che ne caratterizzano dimensioni e posizione]; analogamente il segmento viene memorizzato attraverso l'informazione che si tratta di un segmento e le coordinate dei suoi estremi; l'intera figura è memorizzata registrando separatamente le informazioni relative alle due sottofigure. Cliccando sul poligono - vedi (a) - o sul segmento - vedi (b) - si possono edidenziare i punti che caratterizzano le due figure. Volendo - vedi (c) - con il mouse posso posizionare diversamente, l'una rispetto all'altra, le due
sottofigure. Agendo sui punti evidenziati, posso anche cambiare forma o orientamento di ciascuna sottofigura.
[ l'aggettivo vettoriale con cui vengono chiamate queste applicazioni deriva dal fatto che un segmento è interpretato non come un insieme di punti ma come se fosse un  "vettore" applicato (A,v), che ha certe dimensioni (le componenti del vettore libero v) e una certa posizione (il punto di applicazione A), che posso modificare operando con il mouse ]
"vettore" applicato (A,v), che ha certe dimensioni (le componenti del vettore libero v) e una certa posizione (il punto di applicazione A), che posso modificare operando con il mouse ]
Entrambi i tipi di applicazioni consentono di realizzare, oltre a traslazioni (come visto sopra), altre  trasformazioni geometriche:
trasformazioni geometriche:
selezionata una figura (una parte di piano nelle applicazioni "paint", un oggetto con una certa struttura nelle applicazioni "draw") su di essa o su una sua copia (realizzata con un copia/incolla e l'eventuale scelta se sovrapporre la nuova figura in modo "trasparente" o "opaco") si possono operare trasformazzioni di scala, ribaltamenti, rotazioni, "inclinamenti" lungo la direzione orizzontale o verticale (vedi la nota successiva), …
Sotto è illustrato come una una figura (A) può essere sottoposta a (B) un ribaltamento rispetto a un asse verticale, (C) una trasformazione di scala (non monometrica), (D) una inclinamento di 45° lungo la direzione orizzontale mediante una applicazione paint: anche lo spessore delle linee viene modificato. Un'applicazione draw, invece, trasformerebbe solo i punti che caratterizzano la figura e, a partire da questi, costruirebbe le linee che costituiscono la figura nel suo nuovo aspetto.

Molte applicazioni integrano una sottoapplicazione "paint" e una
"draw". Vari programmi per l'elaborazione di testi contengono sottoprogrammi grafici di tipo paint o draw. Un'efficiente applicazione draw è
incorporata nel gratuito Open Office. Esistono anche specifiche applicazioni di geometria dinamica, che consentono di integrare facilmente
modalità di disegno con tecniche algebriche e con tecniche manuali (movimento del mouse). Anche il citato Desmos consente di
integrare le due modalità.
 Nota. Quando, cliccando su un'opportuna icona o operando su un menu a cascata o …, comandiamo l'esecuzione di una trasformazione, l'applicazione la esegue operando sulle coordinate della figura (sulle coordinate-schermo dei pixel che la compongono o sulle coordinate dei punti che la caratterizzano, a seconda dell'applicazione) mediante una opportuna funzione a 2 input e 2 output (ne abbiamo visto alcuni esempi alla voce
Nota. Quando, cliccando su un'opportuna icona o operando su un menu a cascata o …, comandiamo l'esecuzione di una trasformazione, l'applicazione la esegue operando sulle coordinate della figura (sulle coordinate-schermo dei pixel che la compongono o sulle coordinate dei punti che la caratterizzano, a seconda dell'applicazione) mediante una opportuna funzione a 2 input e 2 output (ne abbiamo visto alcuni esempi alla voce  trasformazioni geometriche).
trasformazioni geometriche).
Vediamo meglio che cosa è un inclinamento lungo una direzione, come quello considerato sopra che ha trasformato (A) in (D) o come quello che trasforma il pesce sotto a sinistra nel pesce sotto a destra. Questo tipo di trasformazione è chiamato anche deformazione lineare o, in inglese, shearing, che significa "tosatura": il suo effetto assomiglia a quello prodotto da una macchina tosatrice o tagliaerba: i peli o i fili d'erba vengono inclinati uniformemente lungo la direzione in cui passa la macchina. L'effetto può essere descritto più precisamente come quello che subisce la figura disegnata su un rettangolo di gomma quando questo viene deformato facendolo diventare un parallelogramma di uguale altezza e uguale base, ovvero su un rettangolo costituito da tante striscioline che poi vengono fatte scorrere in modo che le loro estremità rimangano allineate (da ciò si deduce che  l'area non viene modificata).
l'area non viene modificata).
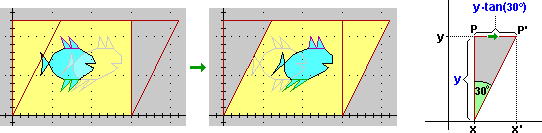
Quello sopra illustrato è un inclinamento orizzontale di 30° e corrisponde alla funzione (x, y) → (x+y·tan(30°), y): la y di ogni punto P della figura rimane immutata mentre la x subisce un incremento proporzionale alla y (x aumenta di y·tan(30°)), la lunghezza del cateto opposto all'angolo di 30° del triangolo rettangolo raffigurato sopra a destra). In maniera analoga si può realizzare un inclinamento lungo la direzione verticale: si tratterà di una funzione del tipo (x, y) → (x, y+x·k) (x non muta e y cresce di una quantità proporzionale a x).
 Variabili indiciate, variabli locali, parametri formali
Variabili indiciate, variabli locali, parametri formali
Abbiamo già usato molte volte
variabili come x0, y4, …, cioè di variabili dotate di indici, o variabili indiciate.
Nei linguaggi di programmazione queste variabili vengono scritte mettendo l'indice tra parentesi, tonde o quadre, a seconda del
linguaggio.
Ad esempio con Desmos
posso introdurre una sequenza di numeri introducendola tra parentesi quadre, usando "," come separatore, comandarne direttamente, ad esempio, la stampa
del minimo, e, indicando l'indice tra quadre (1 per il 1º elemento, 2 per il 2º, ... - altri software usano 0 per il 1º, 1 per il 2º, ...), il valore di un
elemento qualunque della sequenza.
Un altro esempio con Desmos:

| | 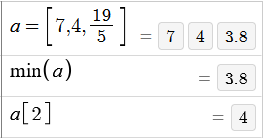 |
La variabile usata nella definzione di f (in questo caso "x") è un
parametro formale:
non è "sostanziale" in quanto l'esecuzione viene fatta non con essa,
ma di volta in volta con al suo posto i termini elencati nelle varie chiamate di f,
che vengono detti argomenti attuali (o parametri reali);
in f(5) l'argomento
attuale è 5.
È qualcosa di analogo a quanto accade quando dico
che  k² sta per k·k
(k sarebbe il parametro formale).
k² sta per k·k
(k sarebbe il parametro formale).
Vediamo un esempio in JavaScript (vedi):
a=3
function F(x) {a=100; return a*(a+1)*x }
b = a*2
document.write(a," ", F(1)," ",F(2)," ", b)
output:
3 10100 20200 6 |
Mentre la variabile a in testa al programma è "condivisa" ("shared" in Inglese) con
gli altri comandi (si dice anche che è una variabile globale), infatti a b viene assegnato il valore 6,
la variabile a presente
nella definizione di F (accanto al parametro formale x) è una variabile locale:
ad essa corrisponde il valore 100 solo all'interno della definizione, ma al di fuori
mantiene il valore 3 che le è stato assegnato inizialmente;
si può anche dire che è una variabile muta:
la sua "voce" non è sentita al di fuori della "function", ossia non può modificare l'assegnazione ad a di precedenti valori.
È analogo
l'impiego della variabile j per descrivere l'insieme dei multipli di 3 con la notazione {j∈N : j/3∈N} (l'insieme dei numeri naturali j tali che la loro divisione per 3 ha come risultato un numero naturale); avremmo potuto descrivere lo stesso insieme con {k∈N : k/3∈N} o usando una qualunque altra variabile al posto di k.
Nota.
Per memorizzare le coordinate di una figura (o altri tipi di informazioni) in modo da poterle utilizzare anche al di fuori dell'esecuzione
di un particolare programma non è sufficiente ricorrere alle variabili indiciate:
occorre registrale in un file.
I linguaggi di programmazione sono dotati di opportune istruzioni per scrivere/leggere file.
Rinviamo ai rispettivi help per altre informazioni.
Vedi qui per applicazioni grafiche varie
 Coordinate schermo (concrete) e cartesiane (virtuali)
Coordinate schermo (concrete) e cartesiane (virtuali) calcolatore (4) abbiamo visto come un'immagine che appare sullo schermo è digitalizzata.
Sotto a sinistra è riprodotto il momento in cui, con un programma per costruire immagini, si sta tracciando un punto-pixel (il puntatore del mouse ha assunto l'aspetto di una matita).
In fondo alla finestra associata alla applicazione appaiono le coordinate-schermo del pixel (29 e 24 in questo caso): sono
i numeri d'ordine della colonna e della riga in cui è collocato; le colonne vengono numerate a partire da sinistra
iniziando con il numero 0; analogamente, a partire dall'alto (non dal
basso!), vengono numerate le righe.
calcolatore (4) abbiamo visto come un'immagine che appare sullo schermo è digitalizzata.
Sotto a sinistra è riprodotto il momento in cui, con un programma per costruire immagini, si sta tracciando un punto-pixel (il puntatore del mouse ha assunto l'aspetto di una matita).
In fondo alla finestra associata alla applicazione appaiono le coordinate-schermo del pixel (29 e 24 in questo caso): sono
i numeri d'ordine della colonna e della riga in cui è collocato; le colonne vengono numerate a partire da sinistra
iniziando con il numero 0; analogamente, a partire dall'alto (non dal
basso!), vengono numerate le righe.