Nella tabella a lato sono riportati gli esiti dei rilevamenti della pressione arteriosa massima in un gruppo di maschi quarantenni (nella colonna 1 i valori, nella 2 le frequenze assolute). I dati sono espressi in millimetri di mercurio (mm Hg) e arrotondati alle cinquine.
Determinane (usando al più una calcolatrice non programmabile) mediana, distanza interquartile, media, varianza e s.q.m.. Controlla eventualmente i risultati utilizzando opportuno software.
951
1001
1052
1103
1155
1206
12510
13015
135  21
140  19
14514
15013
 1558
1605
1654
1703
1753
1802

Dalla tabella con le frequenze ricavo quella con le frequenze cumulate: →
I dati sono 135. Al centro vi è il dato di posto (1+135)/2 = 68. I dati dal 65° all'83° valgono, arrotondati alle cinquine, 140. Posso assumere questa come arrotondamento alle cinquine della mediana.
Volendo [ valori medi 2] posso stimare meglio questo valore riferendomi agli intervalli (vedi la figura seguente):
la mediana cade nell'intervallo [137.5,142.5), ampio 5, in cui cadono 19 dati. 64 sono i dati caduti negli intervalli precedenti. Il segmento verticale che taglia a metà l'istogramma ha ascissa ha da 137.5 una distanza che corrisponde a quanti dati da 64 mancano per arrivare al 50% di 135. La scala per passare dalle distanze in dati a quella in pressioni è 5/19. Quindi come mediana prendo:
137.5+(50%·135-64)·5/19 = 137.5+3.5·5/19 = 138.42… = 138.
L'istogramma poteva essere tracciato a mano; il seguente è tracciato con lo script "istogramma" presente QUI introducendo:  95*1, 100*1, 105*2, 110*3, 115*5, 120*6, 125*10, 130*15, 135*21, 140*19, 145*14, 150*13, 155*8, 160*5, 165*4, 170*3, 175*3, 180*2
951
1002
1054
1107
11512
12018
12528
13043
135  64
140  83
14597
150110
 155118
160123
165127
170130
175133
180135

95
100
105
110
115
120
125
130
135
140
145
150
155
160
165
170
175
180		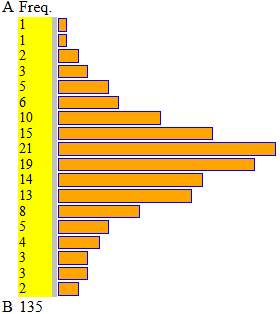 A = 92.5, B = 182.5,  18 intervalli di ampiezza 5

n = 135,  min = 95, max = 180

1^ quarto = 130, mediana = 140, 3^ quarto = 150,  media = 139.259

centri degli intervalli:
95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160, 165, 170, 175, 180

    I valori per mediana e quartile prodotti dal programma sono riferiti al centro degli intervalli. Possiamo stimarne il valore meglio.
    135/4 = 33.75; quindi il 25° percentile (primo quartile) sta tra i dati di posto 28 e 43, e corrisponde quindi a 130 (arrotondamento alle cinquine).  135·3/4 = 101.25 quindi il 75° percentile sta tra i dati di posto 97 e 110, e corrisponde quindi a 150 (arrotondamento alle cinquine).  La distanza interquartile (IQR) è quindi 150-130 = 20 (valore arrotondato alle decine: facendo la differenza le precisioni si sommano).
Posso stimare meglio il valore riferendomi agli intervalli. 127.5+(25%·135-28)·5/(43-28) = 137.5+5.75·5/15 =129.41…;  147.5+(25%·135-97)·5/(110-97) = 149.13…;  149.13-129.41 = 20 (arrotondando alle unità). Quindi il 20 trovato prima ha una precisione migliore della decina.

    Per il calcolo della media, sopra ottenuta con lo script, avrei potuto usare una calcolatrice tascabile.

    Calcoli con un programmino in JavaScript:

x=[95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160, 165, 170, 175, 180]
f=[1, 1, 2, 3, 5, 6, 10, 15, 21, 19, 14, 13, 8, 5, 4, 3, 3, 2]; n=x.length
tot=0; for(i=0; i<n; i=i+1) tot=tot+f[i]
m=0; for(i=0; i<n; i=i+1) m = m+x[i]*f[i]; m = m/tot
document.write("tot = ", tot, " | media = ", m)

tot = 135 | media = 139.25925925925927

    Per trovare lo s.q.m. della nostra distribuzione X posso calcolarlo direttamente usando la definizione, ossia calcolare la media dei quadrati degli scarti (Var(X)) e farne la radice quadrata, oppure, nel calcolo a mano o con una calcolatrice non sofisticata, usare la proprietà: Var(Y) = M(Y²)–M(Y)² applicata alla distribuzione Y ottenuta da X nel modo sopra fatto per il calcolo della media (Y = (X-140)/5):

1*(-9)²+1*(-8)²+2*(-7)²+3*(-6)²+5*(-5)²+…+4*5²+3*6²+3*7²+2*8² =
1*81+3*64+5*49+6*36+9*25+11*16+18*9+28*4+35*1+19*0 =
1444;   M(Y²) = 1444/135;   M(Y)² = (-20/135)²
sqm(X) = sqm(X-140) = sqm(Y)·5 = √(1444/135-(-20/135)²) ·5 = 16.3

Ecco il controllo dei risultati con lo script "calcolatrice2" presente QUI:

mean = 139.25925925925927
variance = 266.85871056241376
scarto quad. medio (sq.root of var./theoret.st.dev.) = 16.335810679682037

Per altri commenti: indici di posizione e dispersione neGli Oggetti Matematici.