Un grande magazzino che vende il prodotto Q per esigenze di pianificazione
vuole individuare una funzione che approssimi il numero di Q venduti complessivamente (anche da altri)
in funzione del tempo. Dispone dei dati seguenti, relativi alle vendite complessive di Q in particolari giorni,
dove il numero di Q è espresso in centinaia:
| giorni | 0 | 20 | 40 | 60 | 80 | 100 | 120 |
| n. di Q | 704 | 550 | 518 | 402 | 391 | 327 | 312 |
Non ha molto senso affrontare con tecniche statistiche questo problema. Vediamo il perché.
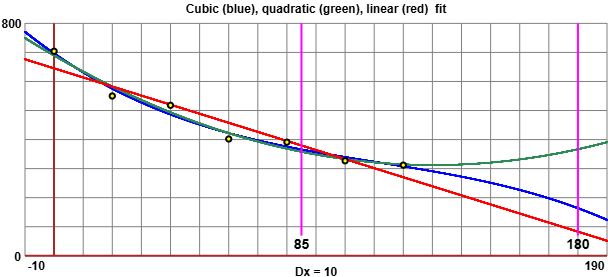
••• Facciamo, inizialmente, i calcoli con WolframAlpha e le rappresentazioni grafiche con uno script. Proviamo ad approssimare i dati con i polinomi di regressione di 3°, 2° e 1° grado.
cubic fit { (0,704), (20,550), (40,518), (60,402), (80,391), (100,327), (120,312) }
y = -0.000145833*x*x*x + 0.0484226*x*x - 6.9506*x + 696.452
quadratic fit { (0,704), (20,550), (40,518), (60,402), (80,391), (100,327),(120,312) }
y = 0.0221726*x*x - 5.78393*x + 689.452
linear fit { (0,704), (20,550), (40,518), (60,402), (80,391), (100,327), (120,312) }
y = 645.107 - 3.12321*x
I grafici con questo script.

Bastano questi esempi per rendersi conto che è minimamente significativo ricorrere in casi come questo a strumenti matematici così raffinati: l'approssimazione mediante una regressione lineare o polinomiale di secondo o terzo grado, come evidenziato dai grafici, danno luogo ciascuna a valori molto diversi quando si esca dal range dei giorni per i quali si hanno i dati; per il 180° giorno si va da 80 a 370; ha senso solo stimare, con po' di buon senso, in circa 370 il numero dei prodotti vednuti l'85º giorno.
L'esercizio è simile ad un esercizio presente su un manuale di statistica, in cui si prospetta, senza alcuna motivazione, la soluzione attraverso una regressione lineare!
••• Per lo studio dei polimoni di regressione di 1º e 2º grado si possono usare anche script presenti qui:
