Per studiare la legge di distribuzione dell'errore delle misure rilevate mediante un radioaltimetro (vedi) si effettuano 400 misure, ottenendo i seguenti risultati:

intervallo  [20,30) [30,40) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100)
frequenza     21      72      66      38      51      56      64      32

Si verifichi (mediante il test χ²) la conformità della distribuzione uniforme con la distribuzione sperimentale.

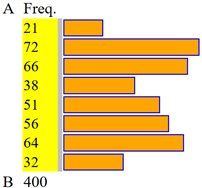
Tracciamo l'istogramma, utilizzando ad esempio lo script "istogramma" presente qui. 25*21, 35*72, 45*66, 55*38, 65*51, 75*56, 85*64, 95*32 percentuali:   |  5.25  |  18  |  16.5  |  9.5  |  12.75  |  14  |  16  |  8  | A = 20,  B = 100,  intervalli = 8 di ampiezza 10 n = 400,   media = 60.25 Tenendo conto della numerosità dei dati e della forma dell'istogramma possiamo supporre che non vi sia conformiltà con la distribuzione uniforme.  Facciamo, comunque, il calcolo di χ² (vedi). Frequenze osservate:   21, 72, 66, 38, 51, 56, 64, 32 frequenze attese:   1, 1, 1, 1, 1, 1, 1, 1 χ² = 45.64

In questo caso i gradi di libertà sono 8-1 = 7.

d.f. 5 10 25 50 75 90 95 7 2.17 2.83 4.25 6.35 9.04 12.0 14.1

45.64 è ben oltre il 95º percentile, 14.1.