Con una complessa apparecchiatura ottengo delle misure (con precisione incerta) del diametro di un particolare oggetto che sappiamo essere sferico ma che non siamo in grado di osservare. Otteniamo i seguenti 30 valori:  1 valore di 11 mm, 1 valore di 12 mm, 3 di 13 mm, 4 di 14 mm, 6 di 15 mm, 5 di 16 mm, 4 di 17 mm, 3 di 18 mm, 2 di 19 mm, 1 di 20 mm.
Dall'istogramma abbiamo che la distribuzione dei valori è approssimativamente gaussiana. Verifica questa cosa con dell'opportuno software e, con lo stesso, verifica se la stessa cosa si può dire dei valori della massa della sferetta ottenibili da essi.

Calcoliamo i cubi. Posso farlo direttamente, ma usiamo la "calcolatrice2" presente qui.

Metto i dati:   11, 12, 13*3, 14*4, 15*6, 16*5, 17*4, 18*3, 19*2, 30   Metto 3 in [Q] e clicco [data^Q].

Traccio i due istogrammi, ad esempio con lo script "istogramma" presente qui.

dati:    11, 12, 13*3, 14*4, 15*6, 16*5, 17*4, 18*3, 19*2, 30
A = 10.5   B = 20.5   n. intervallini = 10
dati:    1331, 1728, 2197*3, 2744*4, 3375*6, 4096*5, 4913*4, 5832*3, 6859*2, 8000
A = 1300   B = 8100   n. intervallini = 8

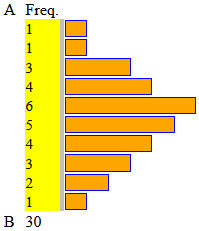A = 10.5   B = 20.5   intervalli = 10 di ampiezza 1 n = 30   min = 11   max = 20   media = 15.6 mediana = 15   1^ | 3^ quarto = 14 | 17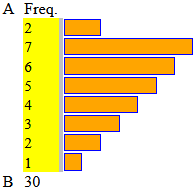

|   |   |   |   |   |   |   |   |   |   |   |

A = 1300   B = 8100   intervalli = 8 di ampiezza 850 n = 30   min = 1331   max = 8000   media = 4007.4 mediana = 3375   1^ | 3^ quarto = 2744 | 4913

Se i diametri delle sferette hanno andamento "gaussiano", i loro cubi (e i valori che siano ottenuti da essi mediante una funzione non lineare) non possono avere andamento gaussiano. Quanto ottenuto con questi script (o anche tracciando gli istogrammi a mano) è sufficiente per rispondere al quesito.

Per altri commenti: Limiti in probabilità neGli Oggetti Matematici.