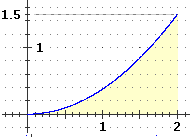
Una variabile casuale ha una legge di distribuzione con densità definita su [0,2] da: x → 3/8x². Verificare che questa è effettivamente una fuzione di densità e determinarne media, mediana, 25° percentile, 75° percentile e scarto quadratico medio. Calcolare la probabiltà che la variabile assuma valori che distino dalla media meno dello scarto quadratico medio.

• A lato è tracciato il grafico delle nostra funzione; chiamiamola h. h(0) = 0, h(2) = 1.5. Per verificare che è una funzione densità calcoliamo ∫_[0,2]f.

∫_[0,2]f = ∫_[0,2]3/8x² dx = [x³/8]_x=2 − [x³/8]_x=0 = 1−0 = 1. OK.
• Media = ∫_[0,2]x·f(x) dx = ∫_[0,2]3/8x³ dx = [3/8x⁴/4]_x=2 = 3/2 = 1.5.
• La mediana è il valore M tale che ∫_[0,M]f(x) dx = 1/2, ossia M³/8 = 1/2, ossia M = ³√4 = 1.5874....
• Il 25° percentile è il numero p tale che ∫_[0,p]f = 1/4, ossia tale che p³/8 = 1/4, ossia tale che p³ = 2, ossia p = ³√2.
• Il 75° percentile è il numero p tale che ∫_[0,p]f = 3/4, ossia tale che p³/8 = 3/4, ossia tale che p³ = 6, ossia p = ³√6.
• Varianza = ∫_[0,2](x−3/2)²·f(x) dx = ∫_[0,2](x−3/2)²·3/8x² dx = 3/20.
Sc. quad. medio = √(3/20) = √15/10 = 0.3872983 (arrotondamento).
• Indichiamo con s lo sc.quad.medio. Dobbiamo valutare ∫_{[3/2−s, 3/2+s]}f.
[x³/8]_x=3/2+s − [x³/8]_x=3/2−s = 0.6680896 (arrotondamento).

( Si noti come [25°percentile, 75°percentile] = [³√2, ³√6] = [1.2599, 1.8171], in cui cade il 50% dei valori, o altri intrevalli riferiti ai percentili, siano in questo caso più significativi dell'intervallo [m−s, m+s] = [1.1127, 1.8873], simmetrico rispetto alla media m senza che questa sia molto vicina alla mediana )

Per altri commenti: Leggi di distribuzione (continue) neGli Oggetti Matematici.

Posso fare tutti i calcoli semplicemente con WolframAlpha:

integrate 3/8*(x^2) dx from 0 to 2
o
integrate [ (3/8*(x^2)) , { x, 0, 2 } ] →

integrate x*3/8*(x^2) dx from 0 to 2 → 3/2 = 1.5

integrate [ (3/8*(x^2)) , { x, 0, M } ] = 1/2 → M^3/8 = 1/2 M = 2^(2/3) ≈ 1.5874

integrate [ (3/8*(x^2)) , { x, 0, M } ] = 1/4 → M^3/8 = 1/4 M = 2^(1/3) ≈ 1.2599

integrate [ (3/8*(x^2)) , { x, 0, M } ] = 3/4 → M^3/8 = 3/4 M = 6^(1/3) ≈ 1.8171

integrate [ (x-3/2)^2*3/8*(x^2) , { x, 0, 2 } ] = 3/4 → 3/20 = 0.15

sqr ( integrate [ (x-3/2)^2*3/8*(x^2) , { x, 0, 2 } ] ) → sqrt(15)/10 ≈ 0.387298

Una variabile casuale ha una legge di distribuzione con densità definita su [0,2] da: x → 3/8x². Verificare che questa è effettivamente una fuzione di densità e determinarne media, mediana, 25° percentile, 75° percentile e scarto quadratico medio. Calcolare la probabiltà che la variabile assuma valori che distino dalla media meno dello scarto quadratico medio.
• A lato è tracciato il grafico delle nostra funzione; chiamiamola h. h(0) = 0, h(2) = 1.5. Per verificare che è una funzione densità calcoliamo ∫_[0,2]f.