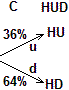1)Un aggregato di persone molto numeroso è composto al 36% da uomini e al 64% da donne.
Sappiamo che per l'altezza HU (in cm) degli uomini si ha M(HU)=174.2 e sqm(HU)=7.1, per quella, HD, delle donne si ha M(HD)=168.1 e sqm(HD)=6.8.
Traccia il grafico della densità di probabilità dell'altezza di questo aggregato di persone e valuta la probabilità che, estraendo con procedimento uniforme una persona, questa sia alta più di 180.3 cm.
2)Problema analogo con bambini coetanei al posto di donne con M(HB)=132.4 e sqm(HB)=5.6.

Nel primo caso, devo studiare la variabile casuale HUD che rappresenta l'altezza di una persona (dell'aggregato considerato) conoscendone la distribuzione sotto la condizione che la categoria C della persona sia "u" (la persona sia un uomo) e la distribuzione sotto la condizione che C="d" (la persona sia una donna). Nel secondo caso C può essere "u" (uomo) o "b" (bambino).

La variabile casuale HUD non è indipendente dalla variabile casuale C. Sia I un intervallo:

–  se C="u", HUD si comporta come HU; cioè (HUD∈I / C="u") equivale a HU∈I;

–  se C="d", HUD si comporta come HD; cioè (HUD∈I / C="d") equivale a HD∈I.
Poiché HUD∈I equivale a (HUD∈I and C="u") or (HUD∈I and C="d"), ho:

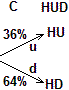Pr(HUD∈I) = Pr(C="u")·Pr(HU∈I) + Pr(C="d")·Pr(HD∈I) = 36%·Pr(HU∈I) + 64%·Pr(HD∈I)

I1 I2 I3 tot

u p₁ p₂ p₃ 100%

d q₁ q₂ q₃ 100%

Volendo, posso rappresentare la situazione anche con una tabella di contingenza: se classifico le altezze in tre intervalli, dalle tabelle di sinistra relative alle due sottopopolazioni passo alla tabella a destra e determino i valori da sostituire a ? sommando le righe "u" e "d".

So che, con buona approssimazione, HU, HD e HB hanno andamento gaussiano.
Poiché, se f è la funzione di densità della variabile continua U, Pr(U∈I) = _a∫ ^b f , posso dedurre che, se UD, U e D sono le funzioni densità di HUD, HU e HD:

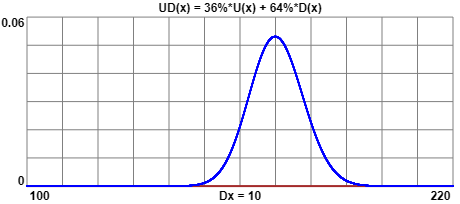
UD(x) = 36%·U(x) + 64%·D(x)

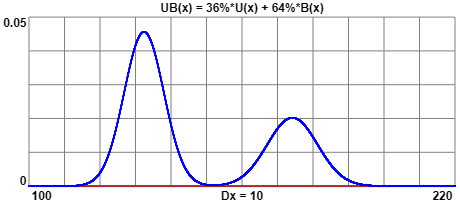
Analogamente, nel caso dei bambini, ho: UB(x) = 36%·U(x) + 64%·B(x)

Sotto sono tracciati (realizzati con questo e questo script) i grafici di UD e UB. Nel caso di UB siamo di fronte a una distribuzione bimodale (ha due massimi relativi). Per la prima situazione non si ottiene una distribuzione bimodale: il grafico di UD è una curva a campana leggermente asimmetrica.