Trova il valore di k, la media e lo scarto quadratico medio della variabile casuale, e la scala del grafico.
|
Una variabile casuale ha una legge di distribuzione con
densità definita su IR del tipo
Trova il valore di k, la media e lo scarto quadratico medio della variabile casuale, e la scala del grafico. |
 |
Per simmetria, l'integrale su (−∞,∞) è
pari al doppio dell'integrale su [0,∞) di
 Leggi di distribuzione (continue) neGli Oggetti Matematici) a k.
L'integrale è dunque 2k. Esso deve essere eguale ad 1, quindi
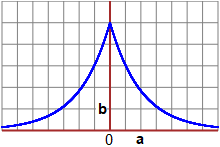
k = 1/2 (e b = 1/2, ed a = 1, in quanto
Leggi di distribuzione (continue) neGli Oggetti Matematici) a k.
L'integrale è dunque 2k. Esso deve essere eguale ad 1, quindi
k = 1/2 (e b = 1/2, ed a = 1, in quanto
Essendo il grafico della densità simmetrico rispetto all'asse y
(ossia essendo la funzione dispari) la media è nulla.
La varianza è
∫ x2e−x dx = −x2e−x−2x e−x−2 e−x (+c); non volendo effettuare questa manipolazione simbolica e da questa ricavare l'integrale definito precedente, possiamo utilizzare WolframAlpha:
compute integral
function: x^2*exp(-x)/2
lower limit: 0
upper limit: inf
1
Per altri commenti:  Leggi di distribuzione (continue) neGli Oggetti Matematici.
Leggi di distribuzione (continue) neGli Oggetti Matematici.