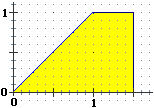
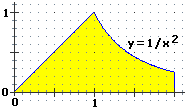
| Gli istogrammi sperimentali di distribuzione di due variabili casuali tendono ad assumere le forme seguenti. Controlla che le aree di queste figure valgono effettivamente 1. Valuta la mediana e la media di queste variabili casuali | |
 |  |
| • Consideriamo la distribuzione a sinistra. L'area è evidentemente 1. La mediana divide a metà l'area dell'istogramma, ovvero l'area "che sta sotto" al grafico della funzione approssimante. Il triangolo a sinistra ha area 1/2, così come il rettangolo. Le due sottofigure sono separate dalla retta x=1. Quindi 1 è la mediana. | |
| Per trovare la media possiamo ragionare geometricamente/fisicamente: il triangolo e il rettangolo hanno la stessa area. Quindi il baricentro, che ha come ascissa la media, è il punto medio tra i due baricentri. Il baricentro del rettangolo ha ascissa 1.25 (al centro del rettangolo), quello del triangolo ha ascissa 2/3 (la media delle ascisse dei vertici), quindi la media cercata è (1.25+2/3)/2 = 0.625+1/3 = 0.958333… | 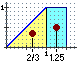 |
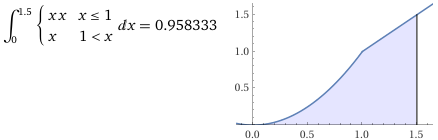
| Posso procedere anche calcolando ∫[0,1.5] x·f(x)dx dove f(x) = x se x<1, f(x) = 1 altrimenti: ∫[0,1.5]x·f(x)dx = ∫[0,1]x·f(x)dx + ∫[1,1.5]x·f(x)dx = ∫[0,1]x·x dx + ∫[1,1.5]x dx = 13/3 + 1.52/2 – 12/2 = 1/3 + 2.25/2 – 1/2 = 1/3 + 9/8 – 1/2 = (8+27-12)/24 = 23/24 (= 0.958333…). | |
Calcoli con WolframAlpha:
integrate piecewise [{ {x*x, x <= 1}, { x, 1 < x} }], x = 0..1.5
| • Anche nel caso della distribuzione a destra l'area complessiva è 1. L'area del triangolo è 1/2. L'area del resto è: ∫[1,2] x–2dx = [–x–1]x=2 – [–x–1]x=1 = –1/2+1 = 1/2. OK. Anche in questo caso la mediana è 1. In questo caso la curva è il grafico di f tale che f(x) = x se x<1, f(x) = x–2 altrimenti. La media è: ∫[0,2] x·f(x)dx = ∫[0,1] x·f(x)dx + ∫[1,2] x·f(x)dx = ∫[0,1]x2 dx + ∫[1,2]x–1 dx = 13/3 + ln(2) – ln(1) = 1/3 + ln(2) = 1.026…. | |
Calcoli con WolframAlpha:
integrate piecewise [{ {x*x, x <= 1}, { 1/x, 1 < x} }], x = 0..2
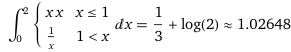
Ovvero: (integrate x*x from x=0 to x=1)+(integrate x*x^-2 from x=1 to x=2)