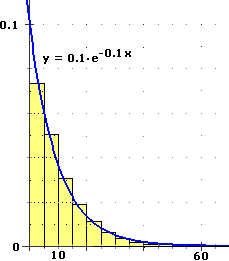
A un servizio telefonico di informazioni arrivano molte telefonate. Sotto è raffigurato l'istogramma di distribuzione del tempo t in secondi che passa tra l'arrivo di una telefonata e quello della successiva.

L'area di ogni rettangolino rappresenta la frequenza relativa con cui i tempi cadono nell'intervallo di base; l'area complessiva dell'istogramma è 100% = 1. Come si vede è più probabile che t sia breve piuttosto che lungo. Il contorno superiore dell'istogramma è stato approssimato col grafico della funzione indicata nella figura. (a) Dimostra che l'area che sta tra grafico della funzione e parti non negative degli assi è 1. (b) Usando la funzione approssimante valuta la probabilità che il tempo di arrivo tra una telefonata e la successiva sia compreso tra 15 sec e 45 sec. (c) Valuta la probabilità che esso sia superiore a 35 sec.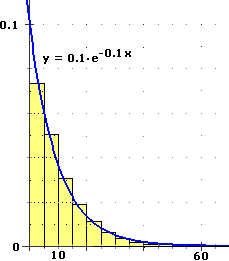

Parte (a).
Consideriamo prima il caso y = h·e^–v·x con h=v=1.
Per simmetria rispetto all'asse y dei grafici di y=exp(x) e y=exp(-x) ho:
∫_[0,k]e^–xdx = ∫_[-k,0]e^xdx = [e^x]_x=0–[e^x]_x=–k = 1–1/e^k

[ Ovvero: Sia t=–x. dt/dx=–1; dx=-dt.
∫_[0,k]e^–xdx = ∫_[0,–k]–e^tdt = –∫_[0,–k]e^tdt =
–([e^t]_t=–k–[e^t]_t=0) = [e^t]_t=0–[e^t]_t=–k = 1–1/e^k ]

Questa è l'area della figura limitata a destra da x=k.
Al tendere di k a ∞ 1–1/e^k tende a 1: la figura illimitata che si ottiene ha area limitata (uguale a 1).

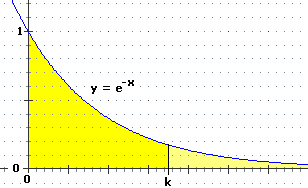Caso generale.
Se moltiplico h per un certo valore Q l'area che "sta sotto a" x → h·e^–v·x viene moltiplicata per Q (la figura scala verticalmente di fattore Q).
Se moltiplico v per un certo valore Q l'area viene invece divisa per Q (la figura scala orizzontalmente di fattore 1/Q). Affinché l'area rimanga 1 occorre che h e v siano uno il reciproco dell'altro.
In altre parole è 1 l'area che sta tra i semiassi positivi e il grafico di x → 1/v·e^–v·x.

Parte (b)
Come probabilità che il tempo in secondi che intercorre tra due telefonate sia compreso tra 15 e 45 assumiamo la frequenza con cui il tempo cade in questo intervallo, ossia l'area dell'istogramma compresa tra questi due valori, che approssimiamo con:
∫_I0.1 e^–0.1xdx, I = [15,45].

∫_[15,45]0.1 e^–0.1xdx = [t=–0.1x, dt/dx=–0.1, dx=-10dt]
–∫_[-1.5,-4.5]e^tdt = –([e^t]_t=-4.5–[e^t]_t=-1.5) = e^-1.5–e^-4.5 = [con la calcolatrice] 0.212 = 21.2%
(controllo con una stima grafica: l'area è circa quella di un triangolo di base 20 e altezza 0.02: 0.02*20/2 = 0.2. OK)

(c) Pr(t > 35) = 1 − Pr( NOT t > 35) = 1 − Pr(t ≤ 35) = 1 − ∫_[0,35]0.1 e^–0.1xdx = 1 − (e⁰–e^-3.5) = e^-3.5 = 0.0301973... = [arrotondando] 3.2%

I calcoli con WolframAlpha:

Parte (b) Come probabilità che il tempo in secondi che intercorre tra due telefonate sia compreso tra 15 e 45 assumiamo la frequenza con cui il tempo cade in questo intervallo, ossia l'area dell'istogramma compresa tra questi due valori, che approssimiamo con: ∫_I0.1 e^–0.1xdx, I = [15,45].
∫_[15,45]0.1 e^–0.1xdx = [t=–0.1x, dt/dx=–0.1, dx=-10dt] –∫_[-1.5,-4.5]e^tdt = –([e^t]_t=-4.5–[e^t]_t=-1.5) = e^-1.5–e^-4.5 = [con la calcolatrice] 0.212 = 21.2%
(controllo con una stima grafica: l'area è circa quella di un triangolo di base 20 e altezza 0.02: 0.02*20/2 = 0.2. OK)
(c) Pr(t > 35) = 1 − Pr( NOT t > 35) = 1 − Pr(t ≤ 35) = 1 − ∫_[0,35]0.1 e^–0.1xdx = 1 − (e⁰–e^-3.5) = e^-3.5 = 0.0301973... = [arrotondando] 3.2%