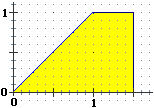
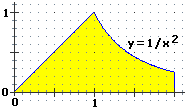
Gli istogrammi sperimentali di distribuzione di due variabili casuali tendono ad assumere le forme seguenti. (1) Controlla che le aree di queste figure valgono effettivamente 1. (2) Traccia i grafici delle corrispondenti funzioni di ripartizione.

La parte (1) dell'esercizio è già stata risolta per affrontarne un altro. Vedila, se non la hai già affrontata.

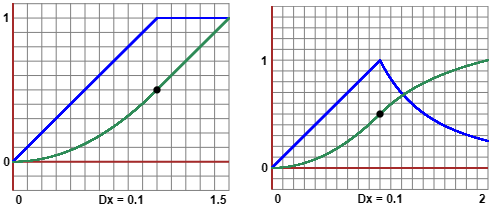
Sotto sono tracciati in verde i grafici delle funzioni di ripartizione.
In entrambi i casi, il primo tratto ha equazione y = x²/2 (la derivata di x → x²/2 è x → x, come l'equazione del primo tratto della funzione densità; inoltre la funzione in 0 vale 0).
Nel primo caso il secondo tratto ha equazione y = x−1/2 (la derivata di x → x−1/2 è x → 1, come l'equazione del secondo tratto della funzione densità; inoltre la funzione in 1 vale 1/2).
Nel secondo caso il secondo tratto ha equazione y = −1/x+1.5 (la derivata di x → −1/x+1.5 è x → 1/x², come l'equazione del secondo tratto della funzione densità; inoltre la funzione in 1 vale 1/2).

[Come faccio a trovare l'equazione della seconda funzione? Vediamo il secondo caso. Devo trovare una funzione che ha come derivata x → 1/x²; essa deve avere la forma x → −1/x+k per qualche k; in 1 deve valer 1/2, quindi −1/1+k = 1/2, da cui k = 1.5]

I grafici precedenti sono stati realizzati con questi script, uno e due.  Avrei potuto anche impiegare WolframAlpha:
plot piecewise [{ {x^2/2, x <= 1}, { x-1/2, 1 < x} }], x = 0..1.5
plot piecewise [{ {x^2/2, x <= 1}, { -1/x+1.5, 1 < x} }], x = 0..2