 |
Delle lastre di lamiera come quella raffigurata a fianco vengono divise in due da uno strumento
che opera un taglio perpendicolare al lato maggiore (nel caso A lo strumento effettua un taglio lungo circa 0.25,
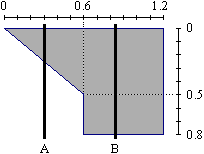
nel caso B effettua un taglio lungo 0.8). Il taglio viene effettuato in una posizione casuale, che si distribuisce uniformemente lungo tale lato; ad esempio, riferendosi al sistema di coordinate raffigurato, la probabilità che il taglio cada tra la posizione 0.2 e la posizione 0.4 è uguale alla probabilità che cada tra la posizione 0.9 e la posizione 1.1. |
| Si studi la distribuzione della lunghezza L del taglio operato e, in particolare, se ne determini il valor medio. | |
|
Poiché 0.6 = 1.2/2,
Pr(L=0.8) = 1/2; L non può assumere altri valori maggiori di 0.5, per cui
Inoltre L ha distribuzione uniforme in [0, 0.5],
cioè: Possiamo calcolare la media M1 in [0,0.5] e la media M2 in (0.5,∞),
ottenendo rispettivamente 1/4 (la distribuzione uniforme tra 0 e 0.5 ha come media il valore centrale) e 0.8
(0.8 è l'unico valore assunto da L superiore a 0.5); quindi fare la media pesata
( M1·Pr(0 ≤ L ≤ 0.5) + M2·Pr(0.5 < L) = 1/4·1/2 + 0.8·1/2 = 0.525. |
Potremmo studiare sperimentalmente L con una simulazione realizzata, ad esempio, con un programmino in Basic:
10 input "n = "; n : s = 0 20 for i=1 to n : x = RND : if x > 1/2 then x = 0.8 30 s = s+x : next 40 print "media = "; s/n : goto 10 n = 100 media = 0.5326549795866008 n = 1000 media = 0.5111723703980484 n = 10000 media = 0.5267160133708018 n = 100000 media = 0.5250677893810571
La media tende a stabilizzarsi intorno a 0.525.
Questa è una variabile aleatoria né discreta né continua.
È una,
cosiddetta, variabile casuale mista.
